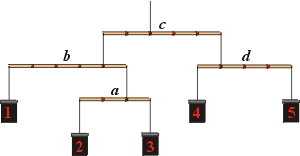
Poměry hmotností krabiček vyjádříme jednoduše z podmínek rovnováhy pro jednotlivé špejle označené na následujícím obrázku písmeny a až d.

Začneme odspoda a hmotnost druhé krabičky si označíme jako jednotkovou m2 = 1. Z momentové věty pro špejli a potom okamžitě vyplývá hmotnost třetí krabičky m3 = 2. Celková hmotnost krabiček na špejli a (neuvažujeme hmotnost samotné špejle) je tedy ma = m2 + m3 = 3. Momentovou větu pro špejli b můžeme nyní podle poměru zavěšení 4:1 zapsat jako
4m1g = mag,
odkud po vykrácení tíhového zrychlení g dostáváme hmotnost první krabičky m1 = 3/4. Celková hmotnost prvních třech krabiček, které zatěžují špejli c je tedy mb = 15/4. Z momentové věty pro špejli c vyplývá podmínka pro zatížení md pravé strany
2mb = 3md,
odkud společná hmotnost čtvrté a páté krabičky je md = 5/2. Jako poslední krok stačí tuto hmotnost rozdělit v poměru 1:3, aby byla splněna podmínka rovnováhy pro špejli d. Hmotnost čtvrté krabičky tak vychází m4 = 15/8, hmotnost páté krabičky m5 = 5/8.
Srovnáním hmotností jednotlivých krabiček zjistíme, že nejtěžší je krabička číslo 3, následují po řadě krabičky číslo 4, 2, 1 a nejlehčí je krabička číslo 5.