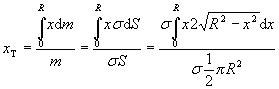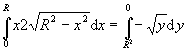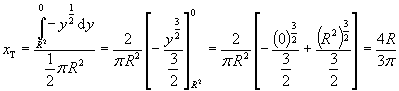Výpočet těžiště polokruhové desky
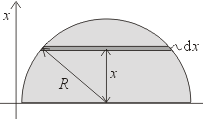 Těžiště polokruhové desky bude ležet (z důvodu symetrie)
na její ose souměrnosti v určité vzdálenosti od rovné hrany. Proto ji
budeme orientovat rovnou hranou kolmo ke zvolené ose x. Desku nyní rozdělíme
na proužky o hmotnosti dm a tloušťky dx kolmé na x, viz
obrázek. Délku proužku můžeme vyjádřit v závislosti na proměnné x
vztahem:
Těžiště polokruhové desky bude ležet (z důvodu symetrie)
na její ose souměrnosti v určité vzdálenosti od rovné hrany. Proto ji
budeme orientovat rovnou hranou kolmo ke zvolené ose x. Desku nyní rozdělíme
na proužky o hmotnosti dm a tloušťky dx kolmé na x, viz
obrázek. Délku proužku můžeme vyjádřit v závislosti na proměnné x
vztahem:
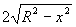
kde R je poloměr desky. Ve vztahu pro výpočet x-ové
souřadnice těžiště desky vyjádříme hmotnost proužku dm a
hmotnost desky m pomocí plochy S a plošné hustoty s,
která se posléze vykrátí:
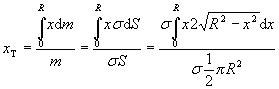
Integrál v čitateli vyřešíme pomocí substituce
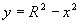 ,
,
ze které derivováním vyplývá
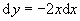 .
.
Při dosazení nezapomeneme přepočítat integrační meze
(dosazením do substitučního vztahu dostaneme dolní mez rovnu R2,
horní mez 0):
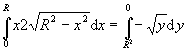
Pro souřadnici těžiště desky ve směru osy x tedy dostáváme:
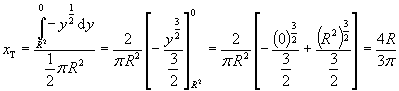
Těžiště polokruhové desky leží na její ose souměrnosti
(na poloměru kolmém k rovné hraně) ve vypočítané vzdálenosti od rovné
hrany, což můžeme snadno ověřit například změřením poloměru vystřižené
papírové desky a jejím vyvážením na špičce tužky.
Zavřít okno
 Těžiště polokruhové desky bude ležet (z důvodu symetrie)
na její ose souměrnosti v určité vzdálenosti od rovné hrany. Proto ji
budeme orientovat rovnou hranou kolmo ke zvolené ose x. Desku nyní rozdělíme
na proužky o hmotnosti dm a tloušťky dx kolmé na x, viz
obrázek. Délku proužku můžeme vyjádřit v závislosti na proměnné x
vztahem:
Těžiště polokruhové desky bude ležet (z důvodu symetrie)
na její ose souměrnosti v určité vzdálenosti od rovné hrany. Proto ji
budeme orientovat rovnou hranou kolmo ke zvolené ose x. Desku nyní rozdělíme
na proužky o hmotnosti dm a tloušťky dx kolmé na x, viz
obrázek. Délku proužku můžeme vyjádřit v závislosti na proměnné x
vztahem: