Co je povrchové napětí

Jednotlivé molekuly vody na sebe působí přitažlivými silami, „lepí se“ k sobě. Důsledkem je například to, že se malé kapičky ochotně spojují ve velké kapky, nebo možnost nalít do nádobky tolik vody, až vytvoří malý kopeček.

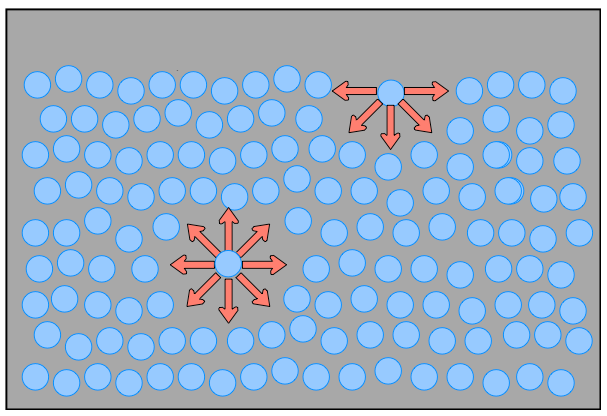
V naprosté většině objemu kapaliny se přitažlivé síly, kterými na nějakou molekulu působí její sousedky, v průměru vyrovnají, jak ilustruje obrázek níže.

Stejný obrázek také ilustruje, jak se liší silové působení pro molekuly blízko povrchu kapaliny. Tam již k vyrovnání nedochází, výsledná síla proto není nulová a míří dovnitř kapaliny.

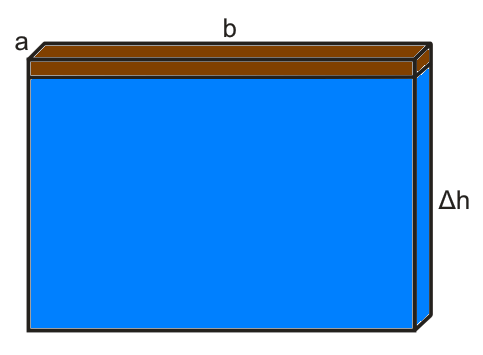
Při přesouvání molekul z vnitřku kapaliny k povrchu tedy musíme překonávat určité síly. Molekuly blízko povrchu proto mají energii označovanou jako povrchová energie. Podobně těleso zdvižené ze země do výšky (zde působíme proti gravitaci) má potenciální gravitační energii.

Povrchová energie je tím větší, čím více se k sobě molekuly v kapalině „lepí“ a roste přímo úměrně s množstvím molekul na povrchu. Označíme-li povrch písmenem S a konstantu určující míru „lepení“ v závislosti na druhu kapaliny jako řecké písmeno sigma σ, můžeme energii jednoduše matematicky vyjádřit jako

E = σ·S

Parametr σ označujeme jako povrchové napětí.

Nyní lze samovolné spojování malých kapiček do velkých kapek vysvětlit také pomocí energie. Systém se snaží mít co nejnižší povrchovou energii, stejně jako se v gravitačním poli příroda snaží umístit předměty tak, aby byla potenciální gravitační energie co nejmenší – předměty samovolně padají dolů.

Teoretický úvod k změření parametru σ odtrhávací metodou

Na povrch hladiny položíme dřevěnou špejli a budeme měřit sílu potřebnou k odtrhnutí špejle z hladiny.

Při vytahování špejle směrem vzhůru vytahujeme spolu se špejlí také „přilepenou“ vodu. Šířku špejle jsem označil a, délku b, výšku vytažené vodní stěny Δh.

Pokud je špejle dostatečně tenká a dlouhá, můžeme objem vytažené kapaliny a s ním i tíhovou sílu zanedbat.

Při vytažení špejle o Δh působíme silou F po dráze Δh, vykonáme tedy práci

W = F·Δh

Tato práce je ovšem rovna energii, kterou jsme přidali povrchové vrstvě:

F·Δh = W = ΔE = σ·ΔS = σ·2(a+b)·Δh

Porovnáme část úplně vlevo s částí úplně vpravo

F·Δh = σ·2(a+b)·Δh

Vydělíme rovnici Δh

F = σ·2(a+b)

A nakonec vyjádříme povrchové napětí σ

σ = F/(2·(a + b))

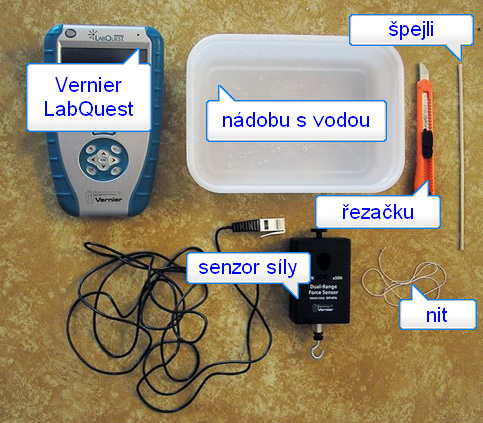
Jak to rychle a snadno provést

Aktivita je inspirována starším článkem Miroslava Jílka. Metoda popsaná M. Jílkem se mi velmi líbí a při dostatku času bych ji s šikovnými žáky určitě zařadil, protože rozvíjí jemnou motoriku a žáci si mohou procvičit řadu dříve získaných vědomostí a dovedností.

Níže popsaná metoda se siloměrem Vernier celé měření výrazně zjednodušuje a zrychluje. Dovolí tedy změřit povrchové napětí i při nedostatku času.

Kromě siloměru Vernier budeme potřebovat rozhraní LabQuest (pro připojení lze použít i libovolné jiné rozhraní Vernier) a dále nádobu s vodou, špejli, nit a řezačku nebo nůž.

Naříznutím konců špejle si připravíme uchycení pomocí niti k siloměru.

Připojíme siloměr k LabQuestu a nastavíme frekvenci měření na 500 Hz.

Nyní položíme špejli na vodní hladinu a chvíli počkáme, aby se nasákla vodou. Poté špejli zavěsíme na siloměr tak, aby se hladiny nedotýkala. Vynulujeme hodnoty, abychom měřili pouze sílu způsobenou povrchovým napětím (a malým zanedbaným příspěvkem gravitační síly vytahovaného sloupce vody).

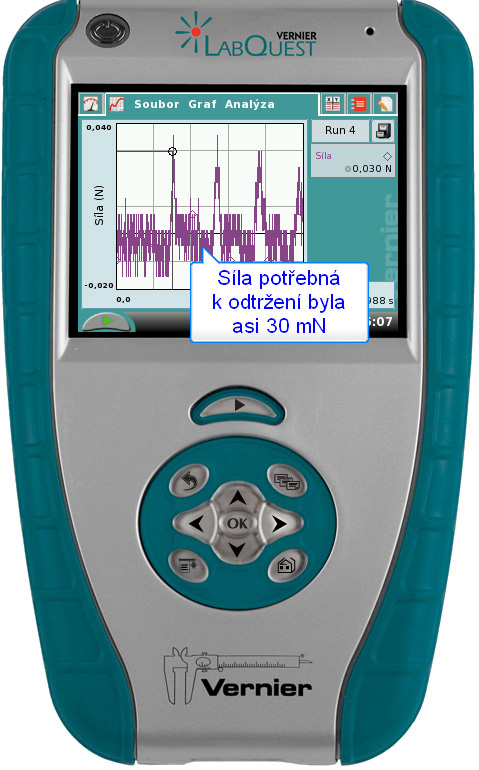
Spustíme měření tlačítkem play a opakovaně pokládáme na siloměru zavěšenou špejli na hladinu a odtrháváme. Odtrháváme pomalu, ne škubnutím. Získáme graf, z jehož maxim můžeme vyčíst velikost síly potřebnou k odtržení špejle od hladiny.

Závěr

Potřebaná síla byla přibližně 30 mN. Po dosazení parametrů mnou použité špejle (délka 133 mm, šířka 3 mm) jsem získal hodnotu povrchového napětí asi 110 milinewtonů na metr. Tabulková hodnota je okolo 70 milinewtonů na metr. S velmi jednoduchou metodou a během chvilky jsem tak získal velmi dobrý odhad povrchového napětí vody.

Další zpřesnění by mohlo být provedeno odhadnutím výšky vytaženého vodního sloupce, vypočítáním příslušného objemu a tíhové síly a odečtením této tíhové síly od změřené hodnoty.

Zpracoval Pavel Böhm