ZÁMĚR ÚLOHY

V této úloze žáci proměří, jak se lze před radiací chránit pomocí dostatečné vzdálenosti od zářiče. Současně úloha umožňuje ukázat náhodný charakter radioaktivního rozpadu i jeho statistickou zákonitost. Užitečný je též přesah do geometrie.

POMŮCKY

• zdroj radiace (školní nebo přírodní zářič)


• detektor alfa, beta a gama záření Vernier VRM-BTD


• datalogger Vernier LabQuest 2 nebo rozhraní LabQuest Mini pro připojení senzoru k počítači

TEORETICKÝ ÚVOD

Zdroj radiace produkuje díky radioaktivní přeměně každou sekundu určité množství záření alfa, beta nebo gama. Toto záření lze detekovat pomocí tzv. Geigerovy-Müllerovy trubice, ve které je část záření zachycena - každý jednotlivý záchyt částice alfa, beta nebo gama se projeví jako impuls. Počet impulsů za daný časový interval je přímo úměrný aktivitě zářiče.

Radioaktivní přeměna je náhodný proces, který se ovšem řídí statistickými zákonitostmi. Počty impulsů tedy sledují určitý trend, ale mohou fluktuovat.

Je-li aktivita zářiče 1000 přeměn za sekundu, znamená to, že každou sekundu je do prostoru okolo zářiče (náhodně do všech směrů) vysláno průměrně 1000 částic alfa, beta nebo gama.

ÚKOLY

1. Zkuste odvodit, jak by měl záviset počet impulsů na vzdálenosti od zářiče.


2. Zjistěte experimentálně, jak závisí počet impulsů na vzdálenosti od zářiče.

Jak provádět měření

1. Připojte senzor radiace VRM-BTD. Pozor, jedná se o digitální senzor, připojte ho tedy do digitálního vstupu LabQuestu nebo LabQuestu Mini.

2. Nastavte dobu měření na 100 sekund.

3. Změřte počet impulsů bez přítomnosti zářiče (takzvané radiační pozadí) a poté se zářičem umístěným v různých vzdálenostech od detektoru - například 2 cm, 4 cm, 6 cm, ... až 16 cm.

4. Ověřte, nakolik je teoretická předpověď shodná s experimentem.

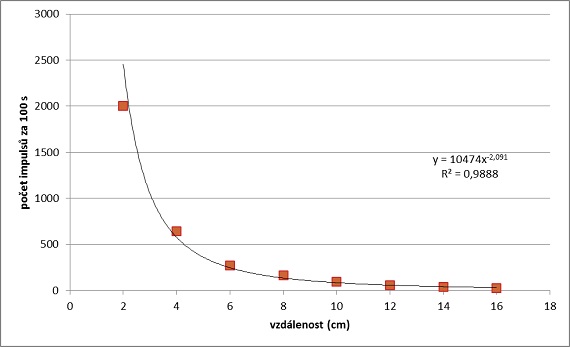
POZNÁMKY PRO UČITELE

Teoretická závislost počtu impulsů na vzdálenosti a souvislost s druhem zářiče

Počet zachycených impulsů za jednotku času by měl ve vakuu klesat s druhou mocninou vzdálenosti. Vysvětlit to lze pomocí geometrické představy.

Zářič za jednotku času vysílá určité průměrné množství částic náhodně všemi směry. Pokud bychom zářič dokonale obklopili detektory se 100% účinností záchytu, zachytily by detektory všechny částice.

Představme si, že detektory tvoří okolo zářiče plášť koule o poloměru 10 cm a jeden detektor má záchytnou plochu 1 cm². Celková plocha detektorů je pak 2·π·r² =1256 cm². K obklopení zářiče ve vzdálenosti 10 cm je tedy potřeba přibližně 1256 detektorů a každý detektor přijímá průměrně 1/1256 z celkového množství částic.

Pokud vzdálenost zdvojnásobíme, počet detektorů musí narůst čtyřnásobně (povrch koule roste s druhou mocninou vzdálenosti). Ve dvojnásobné vzdálenosti tedy jeden detektor zachytí ne polovinu, ale čtvrtinu částic. Ve trojnásobné vzdálenosti to bude devítina atd.

Jelikož experiment neprobíhá ve vakuu, je část záření (částic) pohlcena vzduchem. U alfa záření je pohlcování vzduchem velmi významné, u beta záření méně, u gama záření můžeme pohlcování vzduchem zanedbat. Chceme-li tímto experimentem ukázat pokles s kvadrátem vzdálenosti, je proto vhodné použít gama zářič.

Ukázky výsledků

Měření v každé vzdálenosti a bez zářiče (měření pozadí) doporučujeme dělat několikrát a pracovat s průměrnými hodnotami. Žáci tak získají přehled o fluktuaci hodnot a o tom, nakolik si jimi vlastně mohou být jisti.

Nejprve jsme proměřili aktivitu pozadí. Průměrná hodnota byla 35 impulsů za 100 sekund. Poté jsme postupně měřili v různých vzdálenostech od zářiče.

V tabulkovém editoru jsme poté vytvořili graf a proložili naměřené body mocninnou funkcí. Počítač sám našel nejvhodnější exponent mocninné funkce, vyšla hodnota -2,091, přičemž teoretická hodnota je -2,0 ve vakuu. Shoda je tedy velice přesvědčivá.

Materiál vznikl v rámci projektu Gymnázia Cheb s názvem Příprava na Turnaj mladých fyziků.

Dostupné ze Školského portálu Karlovarského kraje www.kvkskoly.cz.

Autorský tým: Pavel Böhm, Hana Böhmová, Filip Danko, Lucie Filipenská, Petr Kácovský, Věra Koudelková, Daniel Novopacký, Ilona Šimánková, Martin Vlach. Děkujeme i všem ostatním lidem, kteří přispěli k tvorbě materiálů.

Pro případ dalších námětů, komentářů, nalezených chyb a podobně využijte e-mailovou adresu pavel.bohm@mff.cuni.cz