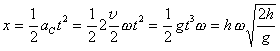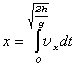FyzWeb  srážky a rotace

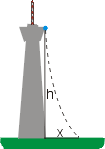
Řešení dopadu kuličky z věže

Těžká kulička padá volným pádem z věže vysoké 80 m stojící na rovníku. Jak daleko a kterým směrem od paty věže dopadne kulička na zem?

 

Výšku věže si označme h, vzdálenost od paty věže do které dopadne kulička x, tíhové zrychlení v daném místě je g. Protože stojí věž na rovníku, nebude mít na pohyb kuličky vliv odstředivá síla, která je rovnoběžná se směrem jejího pohybu.

         Kulička bude tedy odchylována pouze vlivem Coriolisovy síly, která podle vztahu (34) míří na východ (můžeme si to představit tak, že vrcholek věže má o něco větší obvodovou rychlost směrem na východ než pata věže).

         Problém je v tom, že velikost Coriolisovy síly se během pádu kuličky mění, protože se mění rychlost kuličky. Při vypouštění je rychlost nulová, maximální je při dopadu.

Spočítejme úlohu pro odhad a porovnání nejprve zjednodušeně a poněkud nepřesně.

Ze vztahů pro rovnoměrně zrychlený pohyb s nulovou počáteční rychlostí vyplývá, že doba pádu kuličky se dá vypočítat jako

 (42)

Na kuličku působí do boku Coriolisova síla o velikosti 

,

 (41)

a uděluje ji Coriolisovo zrychleni ve vodorovném směru (ve směru x) o velikosti

 

 (43)

Velikost rychlosti pádu kuličky se mění s časem podle vztahu

.

 (44)

Tato rychlost se mění, ale pokud vezmeme její průměrnou hodnotu v/2 – to je naše zjednodušení, bude mít Coriolisovo zrychlení konstantní hodnotu.

        Vzdálenost dopadu kuličky potom můžeme spočítat jednoduše jako dráhu rovnoměrně zrychleného pohybu se zrychlením aC ve vodorovném směru za čas t rovný době pádu kuličky.

 (45)

Pro úhlovou rychlost rotace Země w = 7,3 . 10-5 s-1 a tíhové zrychlení g = 10 m.s-2 vychází vzdálenost dopadu míčku od paty věže přibližně 2,3 cm východním směrem.

? Uměli bychom úlohu spočítat přesně?

Zjednodušili jsme si situaci tím, že jsme uvažovali konstantní průměrnou rychlost pádu kuličky a tím i konstantní velikost Coriolisova zrychlení. Ve skutečnosti Coriolisovo zrychlení závisí na čase a velikost rychlosti kuličky ve vodorovném směru je dána vztahem

.

 (46)

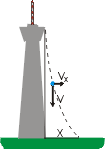
Za velmi (nekonečně) krátkou dobu dt se tedy kulička posune ve vodorovném směru o vzdálenost

.

 (47)

Celkovou odchylku x kuličky ve vodorovném směru bychom pak dostali posčítáním všech elementů dx během doby pádu kuličky, která je dána vztahem (42). Matematicky to můžeme provést pomocí jednoduché integrace, jak už víme z příkladu výpočtů momentu setrvačnosti.

 (48)

Postupným dosazováním potom dostáváme

.

 (49)

Pro zadané hodnoty vychází vzdálenost dopadu kuličky přibližně 3,1 cm východně od paty věže.