Moment hybnosti

Na naši situaci se židlí se můžeme dívat ještě jiným způsobem. Během připažení se změní rozložení hmotnosti našeho těla vůči ose otáčení a změní se tedy náš moment setrvačnosti vůči ose otáčení. Jestliže přitáhneme ruce k tělu - blíž k ose otáčení - náš moment setrvačnosti se zmenší a zároveň vzroste naše úhlová rychlost.

Změna momentu setrvačnosti a změna úhlové rychlosti spolu tedy nějakým způsobem souvisí.

Pokud si rozepíšeme a upravíme součin úhlové rychlosti w a momentu setrvačnosti závaží o hmotnosti m pohybujícího se touto úhlovou rychlostí ve vzdálenosti r od osy otáčení

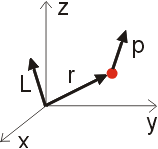
V našem speciálním případě rotace na židli, je vektor obvodové rychlosti v závaží a tedy i vektor hybnosti p závaží kolmý na vektor r určující nejkratší vzdálenost od osy otáčení. Velikost momentu hybnosti je proto rovna prostému součinu rp.

         Směr momentu hybnosti je v tomto případě rovnoběžný se směrem úhlové rychlosti w, jak vyplývá z vektorového součinu (50).

Obecně je vektor momentu hybnosti rovnoběžný s vektorem úhlové rychlosti pouze v některých případech rotace symetrických těles.

Moment hybnosti vystupuje v důležitém vztahu, který se nazývá druhá věta impulsová a jehož odvození lze najít např. v [6]. Druhá věta impulsová vyjadřuje skutečnost, že časová změna momentu hybnosti je rovna celkovému momentu síly působícímu na těleso. Matematicky vyjádřeno:

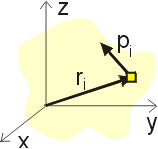
M je celkový moment sil určený vztahem

(F_n jsou uvažované síly, r_n polohové vektory jejich působišť). Změnu momentu hybnosti vyjadřujeme jako jeho derivaci, podobně jako například rychlost je derivace dráhy podle času.

Vztah (52)  připomíná druhý Newtonův pohybový zákon, ze kterého také skutečně vychází, a je jeho obdobou pro soustavu rotujících těles. Uvažujeme-li například náš speciální případ závaží o hmotnosti m rotujícího kolem osy ve vzdálenosti r, můžeme psát druhou větu impulsovou (uvažujeme pouze velikosti vektorů) ve tvaru

Jestliže se vzdálenost r nemění, můžeme ji vykrátit a vztah (54) přejde na druhý Newtonův pohybový zákon

Nyní se můžeme vrátit k vysvětlení pohybu krasobruslaře při piruetě. Z druhé věty impulsové vyplývá, že pokud na krasobruslaře nepůsobí žádný vnější moment síly (M =0), jeho moment hybnosti L zůstává konstantní (změna L je nulová). Předpokládáme-li navíc, že platí vztah (49) L = Jw, potom je zřejmé, že při připažení, kdy se zmenší moment setrvačnosti krasobruslaře, se musí zvýšit jeho úhlová rychlost. 

Na příkladu krasobruslaře jsme sledovali velmi důležitý důsledek 2. věty impulsové.

Komentář pro vyučující

Na obsah