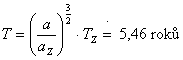|
FyzWeb srážky a rotace |
||||||||||||||||||||
Řešení problému cesty na JupiterStřední vzdálenost Země od Slunce (jednu astronomickou jednotku) budeme pro jednoduchost považovat také za hlavní poloosu eliptické trajektorie Země, přibližně tedy aZ = 1 AU = 149.109 m. Oběžná doba Země TZ je jeden rok, vzdálenost Jupitera od Slunce je přibližně aJ = 5,2 AU.
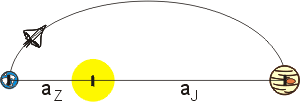
obr. I Dráha kosmické lodi představuje polovinu elipsy, v jejímž jednom vrcholu bližším Slunci (perihelium) je Země v okamžiku startu, ve vzdálenějším vrcholu (afélium) je Jupiter v okamžiku průletu lodi. Hlavní poloosu a této elipsy určíme, viz obr. I, jako
pro uvedené hodnoty a = 3,1 AU. Dobu cesty k Jupiteru můžeme nyní jednoduše určit z třetího Keplerova zákona jako polovinu oběžné doby T lodi po uvažované eliptické trajektorii. Loď se pohybuje stejně jako Země v gravitačním poli Slunce a pro jejich oběžné doby a velikosti hlavních poloos jejich trajektorií můžeme tedy psát:
Oběžná doba lodi potom vychází:
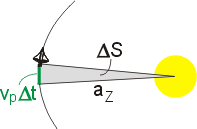
Cesta k Jupiteru by tedy za takových podmínek trvala přibližně dva a tři čtvrtě roku. Rychlost lodi v periheliu (v okamžiku startu) můžeme určit pomocí druhého Keplerova zákona. Tento zákon můžeme chápat tak, že zůstává konstantní takzvaná plošná rychlost C lodi. Ta je dána podílem plochy DS opsané průvodičem planety a času Dt, za který loď tuto plochu opíše.
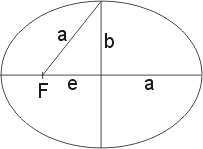
Do vztahu (70) můžeme dosadit za DS plochu celé elipsy S = pab a za Dt příslušný čas jedné periody oběhu T.
vp je rychlost lodi v periheliu. Dosazením vztahu (72) do (70) a porovnáním se vztahem (71) dostáváme:
Pro uvažované hodnoty vychází rychlost lodi v periheliu přibližně 38,68 km.s-1. Protože obvodová rychlost Země kolem Slunce je přibližně 31 km.s-1, stačilo by lodi udělit rychlost necelých 8 km.s-1 ve směru pohybu Země. Poznámky Skutečná situace vypouštění lodi k Jupiteru by byla samozřejmě složitější. Rychlost 8 km.s-1 vzhledem k Zemi je například menší než úniková rychlost při povrchu Země (11,2 km.s-1) a bylo by třeba diskutovat, z jaké výšky nad Zemí je potřeba loď vypouštět. Cesta k Jupiteru by musela být také plánována s ohledem na postavení planet tak, aby loď na konci své cesty zastihla Jupiter apod. Některé problémy podobné cesty k Marsu jsou například řešeny ve studijním textu [9]. |
||||||||||||||||||||