FyzWeb  srážky a rotace

Řešení úlohy s válečkem

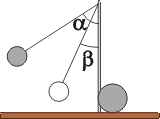
Ocelová kulička o hmotnosti m je zavěšena na vlákně délky l a vychýlena o úhel a od svislého směru. Po vypuštění narazí do ocelového válečku o hmotnosti M a poloměru r, který stojí pod závěsem. Po pružném centrálním nárazu se kulička se závěsem vychýlí zpět o úhel b.

Jakou rychlostí se rozjede váleček po nárazu?


Potenciální energie vychýlené kuličky na začátku vzhledem k její nejnižší poloze je určena vztahem

,

kde g je tíhové zrychlení.

Po nárazu se vychýlí o menší úhel b a její potenciální energie je určena vztahem

.

Rozdíl potenciálních energií EP1 – EP2 je roven celkové kinetické energii válečku, kterou získá při pružné srážce. Tato energie je určena Königovou větou

,

kde v je hledaná postupná rychlost válce.

je moment setrvačnosti válce,

je úhlová rychlost válečku.

Ze zákona zachování energie

potom po dosazení získáme hledanou rychlost válečku

.

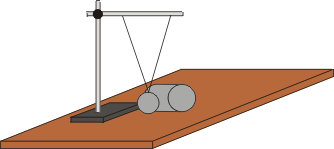
K experimentálnímu ověření potřebujeme ocelovou kuličku s háčkem na zavěšení, o něco těžší ocelový váleček, nit, stojan, váhy, délkové měřítko a stopky.

Kuličku je vhodné zavěsit na bifilární závěs (dvě nitě), aby se kývala pouze v požadovaném směru. Váleček umístíme tak, aby do něj kulička narazila přesně centrálně a váleček se tak rozjel rovně dopředu.   

Úhel vychýlení kyvadla můžeme určit změřením vodorovné odlehlosti kuličky od svislého směru. Rychlost válečku určíme například změřením doby, za kterou váleček urazí předem stanovenou vzdálenost, například 10 cm. Ostatní potřebné veličiny změříme snadno.

Pokus je výhodné provádět minimálně ve dvojici, abychom mohli sledovat zároveň výchylku kyvadla a zároveň rychlost válečku. Celý pokus můžeme také zaznamenat pomocí videokamery (nebo digitálního fotoaparátu s funkcí videozáznamu) a vychýlení závěsu i rychlost válečku odečíst ze záznamu.