Máte představu, kudy z vašeho domu utíká nejvíce tepla?

Částka, kterou dnes platíme za udržení tepla v našich domovech, není rozhodně zanedbatelná. Ať už si pořizujeme nové bydlení, nebo žijeme ve starším domě či bytě, vyplatí se zapřemýšlet nad tím, jak svůj domov nebo třeba chatu tepelně izolovat a do čeho má cenu investovat. Nejde přitom jenom o naši kapsu, ale také o okolní prostředí, které svojí činností do značné míry ovlivňujeme.

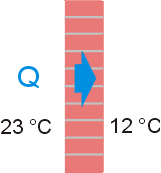
Můžete samozřejmě namítnout, že existují odborníci, kteří vám přesně poradí, co si máte pořídit. Vždy se však hodí, když si dokážete na danou problematiku udělat i vlastní názor a rozhodnout se podle toho, co skutečně chcete, a ne jen podle toho, co je vám doporučeno. (To samozřejmě v žádném případě neznamená, že rady odborníků musí být nějak špatné.)

Podívejme se nejdříve, jak se přenáší teplo jednoduchou stěnou, která má na jedné straně vyšší teplotu než na druhé. Vyšší teplotu si můžeme zjednodušeně představit jako rychlejší pohyb molekul látky. Rychlejší molekuly narážejí do pomalejších, rozkmitávají je a předávají jim tak energii. Tato energie se proto přenáší z teplejší strany na studenější a celému procesu se většinou říká vedení tepla.

Na čem závisí, kolik tepla se přenese materiálem z jedné strany na druhou?

Asi vás napadne, že čím větší bude plocha stěny, kterou může teplo prostupovat, tím více tepla stěnou projde. S tloušťkou stěny to bude zřejmě naopak, protože čím bude stěna silnější, tím hůře se bude teplo předávat prostřednictvím pohybu molekul z jedné strany na druhou. 

Kromě rozměrů stěny bude také důležité, z jakého materiálu je stěna vyrobena (některé látky obsahují atomy, které si předávají energii "snadněji" než atomy jiné látky). Dá se také rozmyslet, že přenos tepla závisí na rozdílu teplot povrchů stěny. Čím větší je teplota jednoho povrchu vůči druhému, tím intenzivnější je pohyb molekul na jedné straně oproti druhé a tím rychleji se předává energie. Nakonec bude zřejmě také důležité, jak dlouho teplo stěnou prochází.

Všechny uvedené závislosti lze shrnout vztahem:

,

kde Q je množství tepla, které projde za dobu t stěnou o ploše S a tloušťce d. Dt je rozdíl teplot na površích stěny a l je tzv. součinitel tepelné vodivosti látky - konstanta, která udává, jak dobrým nebo špatným tepelným izolantem je daný materiál.

Jsou však uvedené závislosti opravdu takto jednoduché?

Není přece vůbec samozřejmé, že uvedené závislosti musí být například lineární, i když to může být na první pohled pravděpodobné.

Pokud tedy chceme s uvedeným vztahem dále počítat, musíme buď věřit, že ho někdo experimentálně dokázal, jak je to popisováno v základních učebnicích termodynamiky, viz literatura (např. [1], [2]), nebo se můžeme pokusit některé závislosti experimentálně ověřit sami.

Nyní už můžeme řešit praktické příklady. Snadno například spočítáme, jaké množství tepla unikne za hodinu cihlovou stěnou dlouhou 4 m, vysokou 3 m a silnou 40 cm, jestliže na jedné straně je povrchová teplota 25 °C a na druhé 5 °C. Je-li součinitel tepelné vodivosti cihel podle tabulek například 0,6 W.m^-1.K^-1, dostaneme po dosazení do vztahu pro množství tepla, které projde za daný čas stěnou, hodnotu 21,6 kJ.

Dokážete podobně spočítat kolik tepla unikne za půl dne z jednoduchého domku 10 m dlouhého a 6 m širokého? Obvodové zdi z cihel jsou vysoké 2,5 m a silné 40 cm. Podlahu tvoří 0,5 m silný beton o tepelné vodivosti 1,5 W.m^-1.K^-1, téměř plochá oplechovaná střecha je zateplena 10 cm silnou skelnou vatou o tepelné vodivosti 0,05 W.m^-1.K^-1. Průměrná venkovní teplota je -2°C, teplotu uvnitř udržujeme na 21°C. Jaký výkon musí mít topení, aby udrželo v domě požadovanou teplotu? (řešení)

V praxi si často nevystačíme pouze se vztahem pro průchod tepla jednoduchou stěnou. 

Co když je například k cihlové stěně přidána polystyrénová izolace? 

Podívejme se, co platí pro průchod tepla takovou dvojitou stěnou. Součinitele tepelné vodivosti cihel a polystyrénu si označíme l₁ a l₂, tloušťky stěn budou d₁ a d₂, teplota na vnějším povrchu cihel bude t₁, mezi stěnami t₂ a na druhém povrchu polystyrénu t₃.

Množství tepla Q, které projde za jednotku času danou plochou (například 1 m²) cihlové stěny, projde i 1 m² polystyrénové stěny (teplo se mezi stěnami nikam neztratí). Můžeme proto při daném označení psát:

Stejné teplo projde celou dvojitou stěnou a platí tedy také:

l je celkový součinitel tepelné vodivosti dvojité stěny a d = d₁ + d₂.

Nyní můžeme vyjádřit rozdíl teplot jako

a dosadit z předchozích vztahů

.

Po vykrácení Q dostáváme výsledný vztah pro součinitele teplotní vodivosti:

Poměr tloušťky stěny a součinitele teplotní vodivosti  d/l se většinou označuje jako tepelný odpor R. To je dobře pochopitelné, protože čím tlustší je stěna a čím menší je součinitel tepelné vodivosti, tím méně tepla stěnou projde - klade teplu větší odpor.

Poslední vztah tak můžeme zapsat jako

,

kde R₁ a R₂ jsou tepelné odpory cihlové a polystyrénové stěny zadaných tloušťek. Celé odvození je potom analogické odvození výsledného elektrického odporu sériového zapojení dvou dílčích odporů.

Konkrétní příklad: Cihlovou zeď o tloušťce 0,4 m a součiniteli teplotní vodivosti 0,6 W.m^-1.K^-1 zateplíme 5 cm silnou polystyrénovou deskou o součiniteli teplotní vodivosti 0,16 W.m^-1.K^-1. Zajímá nás, jak se změní izolační schopnosti stěny.

Tepelný odpor samotné cihlové stěny je podíl její tloušťky a jejího součinitele teplotní vodivosti a je tedy přibližně R₁ = 0,67 m².K.W^-1. Obdobně tepelný odpor polystyrénové desky je přibližně R₂ = 0,31 m².K.W^-1. Výsledný tepelný odpor izolované stěny je R = 0,98 m².K.W^-1, z čehož je vidět, že přidáním polystyrénu se izolační vlastnosti stěny zlepšily asi o polovinu oproti samotné cihlové zdi. To znamená, že za stejný čas projdou zaizolovanou stěnou dvě třetiny původního množství tepla a náklady na vytápění se sníží o třetinu.

Pokud bychom chtěli vědět, jaké množství tepla projde za hodinu zaizolovanou stěnou o ploše například 12 m² při rozdílu teplot na jedné a druhé straně 20 °C, dosadíme opět do vztahu, kde je podíl d/l nahrazen výsledným tepelným odporem:

Výkon tepelného zdroje potřebný k takovému toku tepla je:

Stejný způsob, kterým jsme odvodili výsledný tepelný odpor dvojité stěny, můžeme použít pro libovolný počet vrstev na sobě. Výsledný tepelný odpor je vždy součtem tepelných odporů jednotlivých vrstev. Nestačí tedy počítat pouze se součiniteli teplotní vodivosti, ale také s tloušťkou stěn.

Zřejmě nejkomplikovanějším prvkem domu z hlediska zateplení jsou okna. Podívejte se, co vše je zde potřeba brát v úvahu.

Náměty pro vyučující

Literatura

Zpracováno na základě podkladů Miroslava Jílka.

Původní materiál naleznete na http://fyzweb.cuni.cz/dilna/krouzky/uvod/uvodni.htm.