|
FyzWeb síly |
||||||
Řešení úlohy s kostkamiJak daleko přes okraj stolu mohou maximálně přesahovat čtyři stejné kostky narovnané jedna na druhé na stůl, aby nepřepadly? Vypočítáme, jak daleko můžeme posunovat jednotlivé kostky. Budeme přitom postupovat shora dolů. Horní kostka má těžiště v polovině své délky. Můžeme ji tedy posunout maximálně o tuto vzdálenost. Pokud ji posuneme ještě dál, vodorovná vzdálenost těžiště horní kostky přesáhne hranu kostky pod sebou a kostka spadne. Označíme-li si délku jedné kostky l, můžeme horní kostku posunout maximálně o l/2.
Protože mají všechny kostky stejnou hmotnost m, platí pro velikosti tíhových sil F1 = F2 = mg. Pro vzdálenost xT těžiště dvou horních kostek od zvoleného počátku (osy otáčení) vychází po vykrácení tíhového zrychlení g
odkud maximální délka převisu ze dvou kostek je:
takže vzdálenost těžiště tří kostek od hrany nejdále vysunuté horní kostky je nyní rovna:
Zcela stejně nakonec zjistíme, jak daleko je možné posunout všechny čtyři kostky přes hranu stolu, aby převis ještě nespadl. S využitím předchozího výsledku těžiště tří kostek platí pro maximální možné posunutí
odkud výsledná vzdálenost těžiště čtyř kostek a tedy i maximální délka převisu vychází
Celou dobu jsme počítali pouze vodorovnou vzdálenost těžiště od vysunuté hrany horní kostky, svislá vzdálenost těžiště bude vždy v polovině výšky uvažovaného "sloupečku" kostek, což na řešení naší úlohy nemá vliv. Jak bude vypadat převis z obecně n kostek?
Podívejme se, jak velké jsou jednotlivé přesahy kostek. Pro jednoduchost si zvolíme délku jedné kostky rovnou dvěma (libovolným jednotkám). Přesah horní kostky přes druhou je tedy 1. Přesah druhé kostky od shora přes třetí je podle výše uvedených výpočtů 1/2, přesah třetí přes čtvrtou 1/3 a přesah čtvrté kostky přes stůl je 1/4. Celková délka převisu je tedy 1 + 1/2 + 1/3 + 1/4, což je 25/12, tedy 25/24 délky kostky. Vypadá to, že celková délka převisu narovnaného z n kostek bude rovna
Pokud bude délka jedné kostky jiná než 2, stačí výsledek pouze vynásobit odpovídající konstantou (například pro 6 cm dlouhé kostky vynásobíme výsledek třemi a vyjde nám délka převisu v cm). To, že se přesahy jednotlivých kostek opravdu zmenšují podle napsané řady, není samozřejmé a je potřeba to dokázat. Důkaz provedete poměrně snadno pomocí matematické indukce (řešení úlohy je možné nalézt například zde). Uvedená řada pro výpočet délky převisu se nazývá harmonická a je zajímavá například tím, že má nekonečný součet, to znamená, že s rostoucím n přesáhne její součet libovolně velké číslo. Pokud budeme mít neomezené množství kostek, můžeme tedy překvapivě narovnat (alespoň teoreticky) libovolně dlouhý převis. Takový převis bude ovšem mnohem větší na výšku než na délku. Například převis z cihel dlouhý 1,45 m (pět standardních cihel vedle sebe) by musel být vysoký více než 17 km!
|
||||||


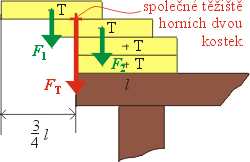 Dále budeme posunovat dvě horní kostky. Abychom věděli, jak daleko mohou
být vysunuty, musíme spočítat polohu jejich těžiště (pouze vodorovnou
vzdálenost). Moment výsledné tíhové síly FT dvou
kostek vzhledem k vybrané ose otáčení (stanovíme si ji například ve vzdálenosti
vysunuté hrany horní kostky) je roven součtu momentů tíhových sil F1,
F2 obou kostek. Pro velikosti momentů tedy píšeme:
Dále budeme posunovat dvě horní kostky. Abychom věděli, jak daleko mohou
být vysunuty, musíme spočítat polohu jejich těžiště (pouze vodorovnou
vzdálenost). Moment výsledné tíhové síly FT dvou
kostek vzhledem k vybrané ose otáčení (stanovíme si ji například ve vzdálenosti
vysunuté hrany horní kostky) je roven součtu momentů tíhových sil F1,
F2 obou kostek. Pro velikosti momentů tedy píšeme: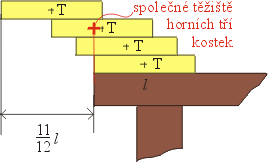 Podobně spočítáme maximální vysunutí tří horních kostek. Využijeme
přitom toho, že už známe polohu těžiště horních dvou kostek. Opět bude
platit, že moment výsledné tíhové síly třech kostek je roven součtu
momentu tíhové síly dvou horních kostek plus momentu tíhové síly třetí
kostky. Po vykrácení g můžeme tedy psát
Podobně spočítáme maximální vysunutí tří horních kostek. Využijeme
přitom toho, že už známe polohu těžiště horních dvou kostek. Opět bude
platit, že moment výsledné tíhové síly třech kostek je roven součtu
momentu tíhové síly dvou horních kostek plus momentu tíhové síly třetí
kostky. Po vykrácení g můžeme tedy psát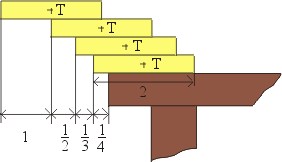 Z rovnání prvních čtyř kostek vidíme, že přesahy
jednotlivých kostek postupně klesají shora dolů. Nabízí se tedy otázka,
jaký nejdelší převis by bylo teoreticky možné narovnat, pokud bychom měli
k dispozici neomezené množství kostek.
Z rovnání prvních čtyř kostek vidíme, že přesahy
jednotlivých kostek postupně klesají shora dolů. Nabízí se tedy otázka,
jaký nejdelší převis by bylo teoreticky možné narovnat, pokud bychom měli
k dispozici neomezené množství kostek.