|
FyzWeb síly |
||||||||||||||
Poloha těžiště
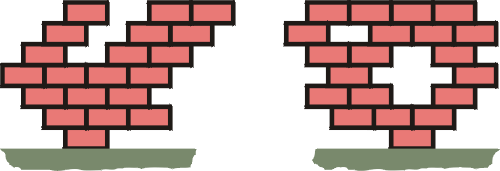
Vezměte si čtyři kostky domina, nebo podobné kvádříky (kostky, krabičky od kazet, knihy...) a pokuste se je narovnat na sebe (jednu na druhou) na kraj stolu tak, aby vrchní kostka přesahovala o co největší vzdálenost okraj stolu. Jak narovnat kostky, abychom vytvořili co nejdelší "převis", který ještě nespadne?
Uměli byste spočítat délku maximálního převisu? Troufnete si odhadnout, jaký nejdelší převis byste byli schopni teoreticky vytvořit, pokud byste měli k dispozici neomezené množství kostiček? A jak by byl takový převis vysoký? Jistě jste si všimli, co musí platit pro polohy kostek, aby náš převis nespadl. Kostky musíme rovnat na sebe tak, že se celkové těžiště všech kostek stále nachází nad deskou stolu. Jakmile vodorovná vzdálenost celkového těžiště přesáhne okraj stolu, přestane být převis v rovnováze a spadne. Stejně nesmí například těžiště dvou horních kostek přesáhnout okraj kostky pod sebou. Každá kostička má symetrický tvar. Snadno tedy uhodneme, že těžiště jedné kostky se nachází přesně v jejím středu. Jak ale určíme polohu těžiště nepravidelného tělesa?
Dokážete určit, kde bude ležet těžiště takové "činky"? Asi odpovíte, že vzdálenost těžiště od menší kuličky bude třikrát větší než vzdálenost od větší (třikrát těžší) kuličky. Pojďme se přesvědčit, jestli tomu tak skutečně je a proč.
Zvolíme si libovolně osu otáčení - například ve středu menší kuličky a napíšeme momentovou větu pro všechny síly vůči této ose. Moment výsledné tíhové síly FT se musí rovnat součtu momentů sil F1 a F2. Pro velikosti momentů potom dostáváme
a po vykrácení tíhového zrychlení g:
Souhlasí spočítaná vzdálenost těžiště s hodnotou určenou pokusem?
Z rovnosti momentů sil nyní po vykrácení tíhového zrychlení dostáváme vztah
kde x3 = 15 cm je vzdálenost těžiště špejle od osy otáčení. Pro upravenou polohu těžiště vychází:
Tato hodnota už by měla odpovídat poměrně přesně poloze těžiště zjištěné vyvážením na noži. Záleží samozřejmě na tom, jak přesně jsme měřili jednotlivé hodnoty.
Nyní už byste měli být schopni spočítat, jaký nejdelší převis lze
postavit ze čtyřech kostiček domina. "Otrlejší povahy" se mohou
pokusit spočítat matematicky obtížnější úlohu - jak dlouhý a vysoký převis
lze narovnat z n kostiček. Obdobně, jako předchozí příklady bychom uměli spočítat polohu těžiště libovolné soustavy těles o hmotnostech m1, m2,...,mn. Pokud jsou vzdálenosti těžišť jednotlivých těles od zvoleného počátku v jednom určitém směru (např. vodorovně, nebo svisle) x1, x2,...,xn, platí pro vzdálenost těžiště celé soustavy xT:
a odtud vzdálenost těžiště soustavy od zvoleného počátku v daném směru:
Obr. I Obr. II Podařilo se vám spočítat, zda zdi spadnou nebo ne? Podívejte se na výsledek.
|
||||||||||||||



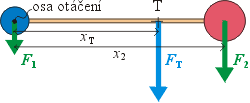 Těžiště tělesa je působištěm výsledné tíhové síly působící na
toto těleso. V našem případě působí na plastelínové kuličky o
hmotnostech m1 a m2 v jejich středech tíhové
síly o velikostech F1 = m1 g
a F2 = m2 g.
(g = 10 m.s-2 je přibližná velikost tíhového
zrychlení) Výsledná tíhová síla působící v těžišti je tedy vektorovým
součtem sil F1 a F2 a musí mít
na těleso stejný otáčivý účinek jako tyto síly.
Těžiště tělesa je působištěm výsledné tíhové síly působící na
toto těleso. V našem případě působí na plastelínové kuličky o
hmotnostech m1 a m2 v jejich středech tíhové
síly o velikostech F1 = m1 g
a F2 = m2 g.
(g = 10 m.s-2 je přibližná velikost tíhového
zrychlení) Výsledná tíhová síla působící v těžišti je tedy vektorovým
součtem sil F1 a F2 a musí mít
na těleso stejný otáčivý účinek jako tyto síly.
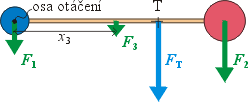 Pokud ne přesně, mohlo by to být způsobeno tím, že jsme si vůbec nevšímali
hmotnosti špejle, která také ovlivňuje polohu těžiště. Uvažujeme-li
hmotnost špejle přibližně m3 = 1 g (
Pokud ne přesně, mohlo by to být způsobeno tím, že jsme si vůbec nevšímali
hmotnosti špejle, která také ovlivňuje polohu těžiště. Uvažujeme-li
hmotnost špejle přibližně m3 = 1 g (