|
FyzWeb síly |
||||||
Výpočet určitého integrálu
Drobná čísla pod a nad symbolem integrálu jsou takzvané integrační meze, které vyjadřují, od jakých hodnot do jakých se mění proměnná x, podle které integrujeme. Při výpočtu integrálu můžeme vytknout všechny konstanty před integrál - stejně jako vytýkáme stejné členy ze součtu před závorku:
V integrálu nám tak zůstala pouze funkce x2, dx je už nyní z matematického hlediska pouze symbol označující integrační proměnnou. Funkci x2 nyní zintegrujeme (přesněji se říká, že k ní najdeme primitivní funkci) jako:
Primitivní funkce k některým základním funkcím můžete najít například v tabulkách i bez toho abyste přesně rozuměli, jak byly odvozeny. Všechny mocniny se například integrují tak, že mocninu zvýšíme o jedničku a výraz vydělíme tímto zvýšeným mocnitelem:
V praxi je pak ještě potřeba naučit se, jak se integrují například složené funkce a součiny pomocí různých substitucí apod. Vraťme se nyní k našemu integrálu. Zbývá nám dosadit do primitivní funkce integrační meze. Prakticky to znamená, že do získaného výrazu nejdříve dosadíme za proměnnou x horní mez a odečteme od něho stejný výraz s dosazenou dolní mezí (vytknuté konstanty samozřejmě opíšeme). Zápis pak vypadá takto:
Tím je integrace hotová a zbývá upravit celkový výraz pro souřadnici těžiště
kde jsme hmotnost trojúhelníka ve jmenovateli vyjádřili jako součin plošné hustoty a obsahu trojúhelníka. Popsaný způsob výpočtu určitého integrálu samozřejmě není vyčerpávajícím matematickým popisem integrace. Jednotlivé úlohy se budou vždy lišit především funkcí, kterou chceme integrovat a právě nalezení primitivní funkce (tomu se říká též výpočet neurčitého integrálu) bývá u integrace nejsložitější. Ostatní procedury, jako sestavování integrálu, úpravy, nebo dosazování mezí jsou mechanické záležitosti a provádějí se u určitého integrálu (to je zjednodušeně řečeno integrál s mezemi) vždy stejně.
|
||||||


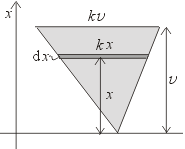 Podívejme se trochu podrobněji na výpočet polohy těžiště trojúhelníkové
desky. Trojúhelník jsme si hned na začátku natočili tak, aby šel rozdělit
na dílky, jejichž velikost lze popsat pouze jedinou proměnnou - v našem případě
x, viz vedlejší obrázek. Integrál jsme sestavili tak, jako by
nahrazoval součtovou sumu s tím rozdílem, že uvažujeme nekonečně mnoho sčítanců
xdm. Symbol dm představuje z fyzikálního hlediska
(nekonečně malou) hmotnost proužku - samotné d tedy není nějakou
proměnnou a samo o sobě nemá žádný význam (nemůžeme ho například krátit).
Protože proměnnou na které závisí délka proužků a tedy i jejich hmotnost
je x, musíme vyjádřit dm pomocí dx. To jsme zařídily
součinem plošné hustoty s a plochy
proužku vyjádřené vztahem xdx.
Podívejme se trochu podrobněji na výpočet polohy těžiště trojúhelníkové
desky. Trojúhelník jsme si hned na začátku natočili tak, aby šel rozdělit
na dílky, jejichž velikost lze popsat pouze jedinou proměnnou - v našem případě
x, viz vedlejší obrázek. Integrál jsme sestavili tak, jako by
nahrazoval součtovou sumu s tím rozdílem, že uvažujeme nekonečně mnoho sčítanců
xdm. Symbol dm představuje z fyzikálního hlediska
(nekonečně malou) hmotnost proužku - samotné d tedy není nějakou
proměnnou a samo o sobě nemá žádný význam (nemůžeme ho například krátit).
Protože proměnnou na které závisí délka proužků a tedy i jejich hmotnost
je x, musíme vyjádřit dm pomocí dx. To jsme zařídily
součinem plošné hustoty s a plochy
proužku vyjádřené vztahem xdx.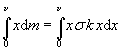
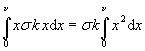
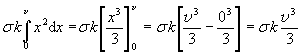
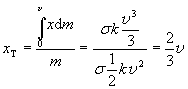 ,
,