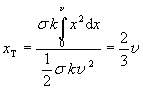|
FyzWeb síly |
|||||||||||
Hmotný střed
Jak to, že se deska nepřeklopí? Pokus je zřejmě obdobný pokusu se smetákem v kapitole o těžišti. Smeták položený na natažené ukazováčky se při přibližování prstů nepřeklopí, protože pod smetákem se posouvá vždy méně zatížený prst, až se prsty sejdou v těžišti. V pokusu s deskou je vidět, že stejný mechanismus funguje i ve dvou rozměrech - při volném pohybu prstů ve dvou nezávislých směrech. Přišli jsme tedy na jeden z experimentálních způsobů, jak nalézt těžiště nepravidelné desky. Dokážeme však polohu těžiště desky spočítat? Nápovědou nám může být opět srovnání pokusu se smetákem a s deskou. V kapitole Převis jsme si ukázali, že poloha těžiště soustavy těles o hmotnostech m1, m2,...,mn, které mají v jednom určitém směru vzdálenosti x1, x2,...,xn od zvoleného počátku je dána vztahem:
xT je vzdálenost těžiště soustavy od zvoleného počátku v daném směru. Uvedeným vztahem bychom mohli (alespoň přibližně) spočítat polohu těžiště třeba právě smetáku tak, že bychom si ho po délce rozdělili na malé kousky o hmotnostech m1, m2,...,mn, viz vedlejší obrázek. Podobný způsob můžeme použít i u desky - rozdělíme si ji pomyslně na malé dílky (čtverečky) o hmotnostech m1, m2,...,mn. Jediný rozdíl je v tom, že u desky musíme uvažovat místo jednoho dva nezávislé směry, ve kterých se vyrovnávají momenty tíhových sil "čtverečků" vůči těžišti. Prakticky to znamená, že musíme spočítat x-ovou a y-ovou souřadnici těžiště podle vztahů
kde x1, x2,...,xn jsou vzdálenosti jednotlivých čtverečků ve směru osy x, y1, y2,...,yn jsou vzdálenosti čtverečků ve směru osy y, m je celková hmotnost desky. Asi cítíte, že to ještě není úplně ono, protože k přesnému výpočtu polohy těžiště bychom potřebovali desku rozdělit na co nejmenší (nekonečně malé) dílky. Přesně to nám však umožní matematická metoda, která se nazývá výpočet určitého integrálu. Můžeme ji použít vždy, když dokážeme popsat nějakou funkcí okraje uvažované desky.
Desku nyní rozdělíme ne na čtverečky, ale na tenké proužky o tloušťce dx a hmotnosti dm kolmé na osu x. Každý takový proužek má totiž konstantní x-ovou vzdálenost. Délka proužku, který má vzdálenost x od zvolené nulové přímky procházející vrcholem trojúhelníku je potom kx. Vzdálenost xT těžiště můžeme nyní spočítat ze vztahu:
m ve jmenovateli zlomku je celková hmotnost trojúhelníku, integrál v čitateli si můžeme zjednodušeně představit jako součet nekonečně mnoha členů xdm, které vyjadřují součin vzdálenosti a hmotnosti jednotlivých proužků. Vidíme tedy, že uvedený vztah odpovídá tomu, co potřebujeme. Hmotnost proužků dm a hmotnost trojúhelníka m ještě vyjádříme pomocí takzvané plošné hustoty s (určuje hmotnost kousku o jednotkové ploše) vynásobené plochou S, abychom mohli integrovat podle proměnné x.
Vidíme, že v čitateli jsme vyjádřili plochu proužku jako jeho délku vynásobenou tloušťkou, ve jmenovateli jsme použili vztah pro výpočet obsahu trojúhelníku (strana krát výška děleno dvěma). Nyní můžeme spočítat polohu těžiště jako:
Pokud jste se nikdy nesetkali s výpočtem integrálů, Výsledek nám ukázal, že nehledě na tvar trojúhelníku leží jeho těžiště ve vzdálenosti 2/3 výšky od vrcholu. Stejný výsledek samozřejmě dostaneme pro libovolnou výšku. To však neznamená, že by těžiště leželo v průsečíku výšek - ty se nemusejí protínat ve 2/3 délky jako těžnice!
Při výpočtu těžiště desky jsme díky vhodně zvolené poloze nakonec nemuseli počítat druhou souřadnici těžiště. To je obvyklá "finta", která se používá abychom si usnadnili práci a nemuseli počítat oba integrály. Asi už vás napadlo, že výpočet polohy těžiště libovolného třírozměrného tělesa se provádí obdobně jako výpočet desky, pouze přidáme poslední souřadnici. Pro souřadnice těžiště tedy platí vztahy:
V je objem daného tělesa o hmotnosti m, je hustota, která však obecně nemusí být konstantní (to je pouze u homogenních těles), ale je funkcí daných souřadnic x, y, z. Vidíme, že uvedené vztahy pro výpočet těžiště nijak nezávisí na gravitaci (nikde se v nich nevyskytuje tíhové zrychlení), proto se bod určený těmito souřadnicemi nazývá přesněji hmotný střed. Jaký je tedy rozdíl mezi těžištěm a hmotným středem? Oba pojmy se často používají pro totéž, rozdíl je v definici. Těžiště jsme si zaváděli jako působiště výsledné tíhové síly působící na jednotlivé části tělesa v tíhovém poli a svým způsobem tedy tento pojem ztrácí význam v beztížném stavu (nezjistíme zde těžiště zavěšením na nit). Hmotný střed je naopak obecný pojem pro bod určený matematicky výše uvedenými vztahy. Prakticky by se poloha hmotného středu mohla odlišovat od polohy těžiště pouze v silně nehomogenním tíhovém poli, což téměř nikdy v praxi nepotřebujeme uvažovat. Nakonec byste se mohli ptát, jak spočítat polohu těžiště u nějakého nepravidelného tělesa (jako třeba sochy moai z úvodní stránky), jehož okraje nejde jednoduše popsat nějakou funkcí. V takovém případě vám nezbude nic jiného než těleso buďto nahradit v jednotlivých částech přibližně stejnými ale geometricky jednoduššími tvary (válce, koule, kvádry...) a spočítat polohu těžiště přibližně, nebo si vyrobit model daného tělesa a určit těžiště experimentálně - například zavěšováním.
|
|||||||||||




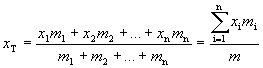 ,
, 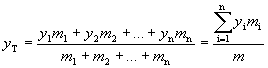 ,
,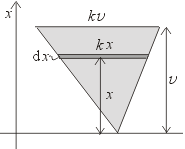 Ukažme si takový způsob na příkladu výpočtu těžiště
desky tvaru trojúhelníku. Desku budeme pro snazší matematický popis
orientovat tak, že jedna strana bude kolmá na zvolenou osu x, viz
vedlejší obrázek. Výšku trojúhelníku na tuto stranu si označíme v.
Délka uvažované strany kolmé na x bude rovna kv
, kde k je konstanta závislá na konkrétním úhlu sevřeném ostatními
stranami trojúhelníku (vyjadřujeme tak lineární funkci popisující okraje
trojúhelníka).
Ukažme si takový způsob na příkladu výpočtu těžiště
desky tvaru trojúhelníku. Desku budeme pro snazší matematický popis
orientovat tak, že jedna strana bude kolmá na zvolenou osu x, viz
vedlejší obrázek. Výšku trojúhelníku na tuto stranu si označíme v.
Délka uvažované strany kolmé na x bude rovna kv
, kde k je konstanta závislá na konkrétním úhlu sevřeném ostatními
stranami trojúhelníku (vyjadřujeme tak lineární funkci popisující okraje
trojúhelníka).