FyzWeb - srážky a rotace

Šikmý ráz

Dvě tělesa se samozřejmě nemusejí srážet pouze centrálně, kdy se jejich těžiště pohybují po jedné přímce. Obecně se mohou srážet pod různým úhlem a takovémuto rázu se říká šikmý. Obdobně jako v případě centrálního rázu je možno ze zákonů zachování hybnosti a energie odvodit obecné vztahy pro rychlosti srážejících se objektů před a po šikmé srážce.

Podívejme se pouze na několik speciálních případů šikmého rázu.

Jeden takový případ dobře znají všichni hráči kulečníku. Jestliže uvedeme jednu kouli na kulečníku do pohybu tak, aby narazila šikmo (tedy ne centrálně) na jinou stojící kouli, rozlétnou se obě koule po srážce vždy pod pravým úhlem. Pouze rychlost každé koule bude záviset na tom, jak „hodně šikmý“ je ráz. Jestliže se strefíme téměř centrálně bude rychlost nalétávající koule mnohem menší než druhé, naopak při téměř tečné srážce odlétne větší rychlostí první - nalétávající koule.

Pokus: O tom se ostatně můžeme snadno přesvědčit buď přímo na kulečníku, nebo pozorováním srážky dvou stejně těžkých kuliček nebo míčků na stole. K lepšímu směrování míčků přitom můžeme použít improvizované tágo z dřevěné laťky – například tyčového metru.

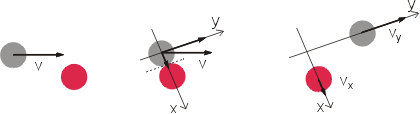
? Jak vysvětlíme takové chování koulí?

Uvažujme nejdříve, že první koule se pohybuje směrem k druhé - stojící kouli rychlostí v, přičemž tato rychlost míří mimo těžiště druhé koule (jde o šikmý ráz). V okamžiku srážky si rychlost v rozdělíme do dvou kolmých směrů viz obr 4. Složka v_x přitom míří ve směru spojnice těžišť obou koulí, složka v_y je na ní kolmá.

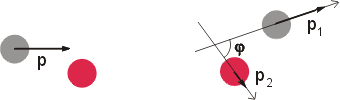
obr. 4

Z toho, co už víme o centrálním rázu dvou objektů, vyplývá, že složka rychlosti v_x se během srážky předá druhé kouli (je to stejný případ jako když jedna koule narazí centrálně do druhé - stojící stejně těžké koule). Výsledkem je, že první koule odlétne po srážce rychlostí v_y, druhá koule rychlostí v_x - tedy kolmo. Zároveň vidíme, že čím víc se bude situace blížit centrálnímu rázu, tím větší bude při srážce složka rychlosti v_x vůči v_y a tím větší bude po srážce rychlost druhé koule vůči první, což je v souladu s naším pozorováním.

Druhou možností, jak chování koulí vysvětlit, je přímo využít zákonů zachování hybnosti a energie. Celková hybnost soustavy před srážkou je dána hybností p první koule před srážkou.

obr. 5

Předpokládejme, že po srážce se koule rozlétnou obecně pod úhlem j, viz obr 5. Velikosti hybností první a druhé koule po srážce jsou

a vektorový součet těchto hybností musí být roven původní hybnosti první koule

Pro velikosti hybností dostáváme s využitím kosinové věty rovnost:

po dosazení

(16)

Považujeme-li srážku za ideálně pružnou, platí také zákon zachování kinetické energie ve tvaru:

(17)

Po vykrácení hmotností m v obou vztazích a polovin ve vztahu (17) vidíme, že řešením této soustavy (za předpokladu nenulových rychlostí v₁ a v₂) je

což splňuje pravý úhel

Druhým řešením soustavy (16), (17) je nulový úhel j = 0, což je případ centrálního rázu koulí.

<< Nepružná srážka

Odraz od stěny >>

Na obsah