Energie rotace - pokračování

Chování plechovek můžeme vysvětlit z hlediska jejich energie. Na začátku mají obě stejnou potenciální energii a nulovou kinetickou energii. Při pohybu po nakloněné rovině se část potenciální energie spotřebuje na kinetickou energii posunu plechovek (danou jejich rychlostí vůči nakloněné rovině) a část na energii jejich rotace. Protože se jedna plechovka pohybuje vůči nakloněné rovině rychleji, znamená to, že spotřebuje méně energie na svoji rotaci.

Připomeňme si, na čem závisí kinetická energie rotačního pohybu.

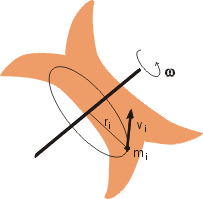
kde v_i je obvodová rychlost tohoto kousku vůči ose daná vztahem

r_i je kolmá vzdálenost kousku špekáčku od osy otáčení.

        Takovýmto způsobem bychom mohli spočítat kinetickou energii všech malých kousků, ze kterých je špekáček tvořen, a celkovou kinetickou energii rotačního pohybu špekáčku bychom získali jako součet všech těchto energií:

Dosadíme-li za obvodovou rychlost ze vztahu (2), dostáváme pro kinetickou energii rotačního pohybu tělesa výraz:

Tento výraz můžeme zjednodušeně zapsat jako

kde veličina

se nazývá moment setrvačnosti tělesa a jak vidíme, je určen rozložením hmoty v tělese. Pokud je hmota soustředěna blízko u osy otáčení, je moment setrvačnosti malý, stejně těžké těleso s hmotou rozprostřenou dále od osy otáčení má moment setrvačnosti větší.

Nyní můžeme přesněji interpretovat výsledek pokusu s plechovkami.

         Plechovky sjíždějí po nakloněné rovině a na úkor své potenciální energie získávají jednak kinetickou energii

danou jejich posuvným pohybem rychlostí v vůči nakloněné rovině, jednak kinetickou energii jejich rotačního pohybu

Pomalejší plechovka tedy spotřebuje více energie na svůj rotační pohyb, což znamená, že musí mít větší moment setrvačnosti. Při stejné hmotnosti musí být tedy hmota uvnitř plechovky rozmístěna více u povrchu plechovky, u rychlejší plechovky je hmota soustředěna blíže osy otáčení, viz podrobnosti k pokusu.

Ještě je třeba upřesnit jednu skutečnost. Při vysvětlení chování plechovek jsme automaticky předpokládali, že potenciální energie plechovky se mění na součet kinetické energie jejího posuvného pohybu a kinetické energie rotace.

            Pokud bychom spočítali celkovou kinetickou energii tělesa, které vykonává zároveň posuvný pohyb s rychlostí v i rotační pohyb s úhlovou rychlostí w, zjistili bychom, že se dá opravdu vyjádřit jako součet kinetické energie posuvného pohybu a kinetické energie rotačního pohybu.

Tento důležitý vztah se nazývá Königova věta a jeho odvození můžeme nají například v [6].

Všimněme si také, že vztah (5) je analogický vztahu pro výpočet kinetické energie posuvného pohybu - místo rychlosti v obsahuje úhlovou rychlost w, hmotnost m je nahrazena momentem setrvačnosti J. Vidíme tedy, že moment setrvačnosti má při rotačním pohybu z energetického hlediska stejný význam jako hmotnost při posuvném pohybu.

? Jak určíme moment setrvačnosti těles některých základních tvarů?

Na obsah