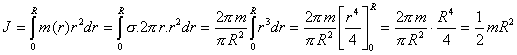Příklady momentů setrvačnosti
|
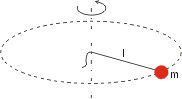
Snadno určíme například moment setrvačnosti malé kuličky o hmotnosti m, kterou točíme na tenkém provázku délky l.
Jestliže je kulička dostatečně malá a hmotnost provázku můžeme zanedbat, je moment
setrvačnosti kuličky |
|
|
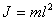
|
(9) |
|
|
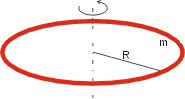
Podobně uhádneme bez počítání i moment setrvačnosti tenkého prstence o hmotnosti m a poloměru R, který se otáčí kolem osy procházející
středem kolmo na rovinu prstence.
Všechna hmota je soustředěna (je-li prstenec zanedbatelně silný) ve vzdálenosti R
od osy otáčení a moment setrvačnosti bude tedy |
|
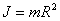
|
(10) |
Už na tomto jednoduchém příkladu vidíme, že moment setrvačnosti není dán pouze tvarem tělesa, ale také polohou osy kolem které těleso rotuje. Pokud by se prstenec otáčel vůči jiné
ose, byla by každá jeho část jinak vzdálena od osy a výpočet momentu setrvačnosti vůči této ose by byl složitější.
|
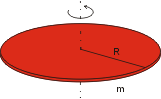
U těles jiného tvaru než jsou zmiňované příklady už se výpočtu nevyhneme. Ukažme si, jak takový výpočet vypadá například při určování momentu
setrvačnosti homogenního disku o hmotnosti m a poloměru R vzhledem k ose procházející kolmo k disku jeho středem. |
|
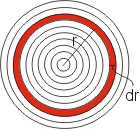
Využijeme toho, že známe moment setrvačnosti tenkého prstence, a rozdělíme si disk na mnoho tenkých soustředných prstenců. Ty budou představovat
kousky hmoty rozprostřené stejně daleko od osy. Sečtením jejich momentů setrvačnosti
potom získáme celkový moment setrvačnosti disku, viz vztah (6).
|
|
Zbývá vyřešit problém, na kolik prstenců máme rozdělit disk. Čím přesněji chceme počítat, tím větší počet prstenců musíme
zvolit.
Pokud chceme počítat zcela přesně, musíme disk rozdělit na nekonečně mnoho nekonečně tenkých prstenců. To jde skutečně udělat
- použijeme-li takzvaný určitý integrál, který nám
v tomto případě zjednodušeně řečeno umožňuje sčítání nekonečně malých kousků. |
Hmotnost m(r) prstence o poloměru r můžeme vyjádřit jako
|
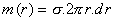 ,
, |
(11) |
kde symbol dr znamená nekonečně malou tloušťku prstence. Součin
|
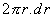
|
(12) |
vyjadřuje plochu prstence a veličina
|
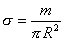
|
(13) |
je plošná hustota disku - to je hmotnost disku o ploše jednoho metru čtverečního.
Moment setrvačnosti disku pak vypočítáme jako
|
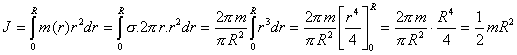 . .
|
(14) |
Pokud jste se dosud s počítáním pomocí integrálů nesetkali, podívejte se, co (zjednodušeně) vyjadřuje předchozí zápis.
|
Moment setrvačnosti jsme počítali pro tenký disk, ale je zřejmé, že tloušťka disku by na výpočtu nic nezměnila.
Hmotnost jsme totiž vyjadřovali pomocí plošné
hustoty (12) závisející pouze na ploše podstavy (tloušťka disku se nám vykrátila).
Vypočítali jsme tak zároveň moment setrvačnosti
pro libovolně vysoký válec o hmotnosti m a poloměru podstavy R vzhledem k ose válce. |

|
|
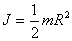
|
(14) |
|
|
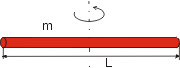
Podobným způsobem bychom mohli vypočítat moment setrvačnosti dalších homogenních těles. Například moment setrvačnosti tenké tyče o hmotnosti m a
délce L počítaný vůči ose procházející kolmo na tyč jejím středem vyjde |
|
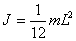 ,
,
|
(15) |
|
|
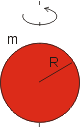
moment setrvačnosti koule o hmotnosti m a poloměru R vzhledem k ose procházející jejím středem je
|
|
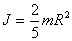 . .
|
(16) |
Na obsah