Ještě o momentu setrvačnosti

V předchozí úloze o tyči odvíjející se od nitě jsme počítali s momentem setrvačnosti tyče vzhledem k ose tyče jako ose válce.           

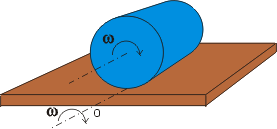
? Jak spolu souvisejí tyto dva pohyby a jaký je moment setrvačnosti válce vzhledem k plášťové přímce o?

Podívejme se na to, jak vypadá kinetická energie válce valícího se rychlostí v vůči podložce.

Ta je dána Königovou větou

kde m je hmotnost válce, J je moment setrvačnosti válce vzhledem k ose válce. w je úhlová rychlost válce vůči jeho ose, ale také je to v daném okamžiku úlová rychlost válce vůči podložce (tj. vůči plášťové ose o).

         Vztah (8) pak můžeme upravit na tvar

kde výraz

vyjadřuje moment setrvačnosti válce vzhledem k plášťové ose o.

Vztah (30) neplatí pouze pro válec a jeho dvě uvažované osy. Obecně lze odvodit, viz např. [6], analogický vztah

který se nazývá Steinerova věta, a který umožňuje vyjádřit moment setrvačnosti libovolného tělesa vůči ose o, jestliže známe moment setrvačnosti J tohoto tělesa vůči ose procházející těžištěm, která je s osou o rovnoběžná ve vzdálenosti d.

Na obsah