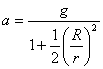FyzWeb - srážky a rotace

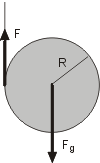
Jo-jo - pokračování

Sílu napínající provázek jo-ja určíme nejdříve ve zjednodušeném případě, kdy je jo-jo tvořeno pouze tyčkou o hmotnosti m a poloměru R, na které je navinuta tenká nit.

Je-li tyč v klidu, působí na nit tíhovou silou o velikosti

(17)

kde g je tíhové zrychlení.

Při pohybu tyče směrem dolů na ni působí jednak tíhová síla F_g směrem dolů, jednak tahová síla nitě F směrem nahoru. Vektorový součet těchto sil uvádí tyč do zrychleného pohybu a pro velikost jejího zrychlení a tedy můžeme z druhého Newtonova zákona psát:

(18)

Abychom určili zatížení nitě, potřebujeme nejdříve zjistit zrychlení a. To můžeme určit ze zákona zachování energie. Úbytek potenciální energie při poklesu tyče o výšku h bude roven celkové kinetické energii, kterou přitom tyč získá.

(19)

(20)

v je rychlost těžiště tyče, J je moment setrvačnosti válce daný vztahem (14), w je úhlová rychlost tyče při poklesu o výšku h.

Dosadíme-li za moment setrvačnosti ze vztahu (14) a za úhlovou rychlost

(21)

dostáváme po vykrácení hmotnosti m a poloměru R

(22)

Ze vztahů pro rovnoměrně zrychlený pohyb s nulovou počáteční rychlostí

(23)

(24)

můžeme vyjádřit rychlost tyče

(25)

a po dosazení do (22) a vykrácení h dostáváme zrychlení tyče

(26)

Dosazením zrychlení (26) do vztahu (18) pak určíme výsledné zatížení nitě

(27)

Jo-jo ve tvaru tyčky odvíjející se od namotané nitě tedy zatěžuje nit třetinovou silou oproti tíze tyčky samotné.

Tento pěkný výsledek by stálo za to experimentálně ověřit.

Pokus: Sílu napínající nit při odvíjení tyčky můžeme změřit pomocí siloměru, případně nějakého počítačového měřícího systému. Podrobnosti

Pokud bychom chtěli určit sílu napínající provázek u skutečného jo-ja válcového tvaru, postupovali bychom stejně jako v případě tyčky. Uvažujme například, že vnější poloměr takového jo-ja je R a poloměr jeho vnitřní části, na které je namotán provázek, je r. Můžeme-li zanedbat hmotnost této vnitřní části, je moment setrvačnosti jo-ja dán opět vztahem (14) a celý výpočet bude stejný až na to, že ve vztahu (21) budeme dosazovat poloměr r, od kterého se odvíjí provázek.

Výsledné zrychlení jo-ja potom vychází

(28)

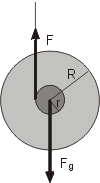
takže například pro šestkrát větší poloměr jo-ja R, než je poloměr jeho vnitřní hřídelky, činí zrychlení pouze 1/19 tíhového zrychlení a tahová síla v provázku bude jen o něco menší než tíha jo-ja.

Tento výsledek bychom mohli samozřejmě také ověřovat pokusem, zde by však vzhledem k malému rozdílu tahové a tíhové síly bylo vhodné použít počítačový měřící systém.

Nyní můžeme odpovědět na naši úvodní otázku, kdy působíme na provázek jakou silou.

Při pohybu jo-ja směrem dolů působíme na provázek menší silou, než je tíha jo-ja. Při pohybu nahoru má zrychlení opačný směr (znaménko u a by se při výpočtech změnilo na opačné) a síla, kterou působíme na provázek, je proto o hodnotu ma větší než tíhová síla.

<< Jo-jo

Ještě o momentu setrvačnosti >>

Na obsah