FyzWeb - srážky a rotace

Speciální případy

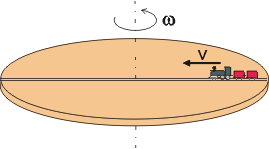
Pokusme se ověřit vztah pro Coriolisovu sílu alespoň ve speciálním případě, kdy rychlost tělesa v otáčejícím se systému míří radiálně - kolmo k ose otáčení vztažné soustavy. To je právě případ míčku při výstřelu z praku namířeného proti nám, viz dřívější pokus, nebo případ Foucaultova kyvadla na pólu.

Uvažujme těleso (například modelový vláček) pohybující se radiálně rychlostí v vůči kruhové desce, která se otáčí doleva (proti směru hodinových ručiček) s konstantní úhlovou rychlostí w. Na začátku je vláček na okraji desky ve vzdálenosti r₁ od osy otáčení.

obr. 3

Podívejme se, jak se změní rychlost vláčku za malý časový interval Dt, viz obr. 3 (vláček si pro pohodlnější znázornění nahradíme hmotným bodem).

Vidíme, že se zmenšila obvodová rychlost vláčku, protože se posunul blíže ke středu - do vzdálenosti r₂. Jestliže jsme uvažovali velmi krátký časový úsek Dt je i úhel pootočení desky velmi malý a obvodové rychlosti na začátku a po pootočení můžeme považovat za téměř rovnoběžné. Rozdíl jejich velikostí pak můžeme zapsat jako

(36)

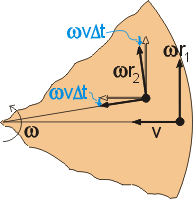
kde jsme rozdíl vzdáleností r₁ a r₂ vyjádřili jako dráhu ujetou vláčkem za čas Dt. Vektor změny rychlosti (36) přitom míří kolmo doleva na směr pohybu vláčku.

Rychlost vláčku v nezměnila svoji velikost, ale změnila poněkud směr. Velikost této změny lze určit stejně jako v případě změny obvodové rychlosti kruhového pohybu při středoškolském odvození dostředivého zrychlení, viz [2]. Pro malý úhel pootočení je velikost této změny rovna

(37)

a směr této změny je opět doleva kolmo na směr rychlosti vláčku.

Celková změna rychlosti vláčku je potom součtem výrazů (36) a (37)

(38)

a má stejný směr jako obě změny.

Nyní můžeme určit velikost zrychlení vláčku jako změnu jeho rychlosti za příslušný velmi krátký čas.

(39)

Na vláček tedy z hlediska „vnější“ inerciální vztažné soustavy působí síla o velikosti

(40)

která způsobuje změnu rychlosti vláčku a míří stejně jako zrychlení kolmo doleva vzhledem ke směru pohybu vláčku. Neuvažujeme přitom dostředivou sílu ve směru pohybu vláčku, kterou působí vlak na desku.

V neinerciálním systému otáčející se desky se vláček pohybuje bez zrychlení, to znamená, že síla F musí být kompenzována zdánlivou setrvačnou silou opačného směru a stejné velikosti.

(41)

Dospěli jsme tedy k výsledku, že na vláček působí v systému otáčející se desky kromě odstředivé síly zdánlivá setrvačná síla (41) kolmo doprava vzhledem k jeho pohybu. Porovnáním vztahů (41) a (35) zjistíme, že se jedná o Coriolisovu sílu – vektor úhlové rychlosti desky a vektor rychlosti vláčku vůči desce spolu svírají pravý úhel.

Pokus: Směr odvozené Coriolisovy síly můžeme ověřit také experimentálně - sledováním dráhy kuličky vystřelované na otáčejícím se kotouči. Podrobnosti

Coriolisovu sílu jsme odvozovali pro případ, kdy se těleso pohybuje radiálně směrem ke středu v otáčející se soustavě. Pokud by se takové těleso pohybovalo radiálně od středu směrem k obvodu, vypadalo by odvození obdobně (můžete si nakreslit příslušný obrázek a odvození si projít) a vyšlo by, že Coriolisova síla působí opět kolmo doprava ke směru pohybu tělesa.

Při pohybu tělesa jiným směrem v otáčející se soustavě bude na těleso působit Coriolisova síla, která je vždy kolmá ke směru pohybu i ke směru vektoru úhlové rychlosti otáčení soustavy. Otáčí-li se soustava doleva bude Coriolisova síla mířit vždy kolmo doprava ke směru pohybu tělesa. Při otáčení soustavy doprava (po směru hodinových ručiček) bude Coriolisova síla mířit kolmo doleva.

V takovém případě už ovšem bude trajektorii tělesa ovlivňovat také odstředivá síla, která míří vždy radiálně od osy otáčení soustavy, a její účinky bychom museli v každém okamžiku přičítat k účinkům Coriolisovy síly.

<< Inerciální a neinerciální soustavy

Projevy Coriolisovy síly na Zemi >>

Na obsah