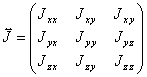Nesymetrická tělesa

Vraťme se ještě jednou k příkladu nevyváženého kola, které znepříjemňuje naši jízdu na kole, nebo třeba v autě. Uvažovali jsme zatím, že osa kola je mírně natočena, takže kolo nemůže rotovat kolem své osy symetrie. Kolo však může být také poněkud zdeformované (například po nárazu) a tedy ne zcela symetrické.

? Jak vypadá rotace nesymetrického tělesa?

Víme už, že rotační pohyb tělesa z dynamického hlediska popisuje vektorová veličina moment hybnosti L, definovaná vztahem (51). Každé rotující těleso také v daném okamžiku rotuje kolem jediné osy, určené vektorem úhlové rychlosti w.

? Jak spolu souvisí tyto dvě veličiny?

Při zkoumání pohybu symetrického setrvačníku jsme počítali s tím, že vektor momentu hybnosti má stejný směr jako vektor úhlové rychlosti, viz vztah (49), a konstantou úměrnosti mezi velikostmi těchto vektorů je moment hybnosti J.          

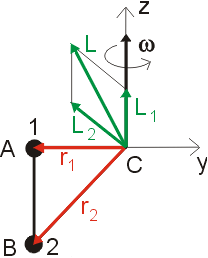
Hybnost první kuličky míří ve směru osy x a její polohový vektor v záporném směru osy y. Moment hybnosti první kuličky L₁ bude tedy podle vztahu (50) mířit ve směru osy z. Moment hybnosti druhé kuličky L₂ však bude podle stejného vztahu mířit šikmo mezi osou z a y (musí být kolmý na vektor hybnosti i polohový vektor). Výsledný moment hybnosti L = L₁ + L₂ proto nemíří ve stejném směru jako vektor úhlové rychlosti.

Protože vektory momentu hybnosti a úhlové rychlosti nejsou obecně rovnoběžné (během rotace se navíc jejich směr i velikosti mohou měnit), nestačí k popisu vztahu mezi nimi jedna konstanta J.

         Jestliže vektor momentu hybnosti má ve zvolené soustavě souřadnic tři složky L_x, L_y a L_z a stejně i vektor úhlové rychlosti w_x, w_y, w_z, potřebujeme k popsání vztahu mezi nimi 3´3 = 9 čísel. Tyto čísla tvoří složky takzvaného tenzoru setrvačnosti, který můžeme zapsat v podobě matice

Každá složka tenzoru setrvačnosti vyjadřuje vztah mezi odpovídajícími složkami vektorů momentu hybnosti a úhlové rychlosti - například:

Složkám J_xx, J_yy, J_zz, které leží na diagonále matice, se říká hlavní momenty setrvačnosti, ostatním složkám se říká deviační momenty. Právě deviační momenty popisují, jak hodně jsou namáhány závěsy nesymetrického otáčejícího se kola.

         Velmi zajímavou vlastností přírody je to, že v libovolně nepravidelném tělese je možné najít tři navzájem kolmé osy – hlavní osy rotace, vůči kterým má tenzor setrvačnosti nenulové pouze hlavní momenty, deviační momenty vůči těmto osám vymizí. Kolem jedné z těchto os bude těleso rovnoměrně rotovat pokud ho necháme volné – tedy pokud na něj nebude působit žádný moment síly.

Pokus: Pokud budete vyhazovat do vzduchu rychle rotující nepravidelné těleso, například pantofel, bude nejochotněji rotovat kolem osy s největším momentem setrvačnosti - kolmo na plochu pantofle. Poznámky

Z toho co jsme si říkali výše je patrné, že u symetrických těles jsou osy souměrnosti zároveň volnými osami, vůči kterým těleso může rovnoměrně rotovat.

Na obsah