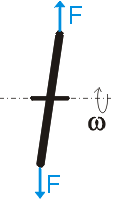Volná osa rotace

Při zkoumání setrvačníků jsme zatím vždy uvažovali symetrický setrvačník, který rotuje kolem své osy symetrie.

? Co se děje se symetrickým tělesem, jestliže ho nutíme rotovat podél různých os? 

Pokud jezdíte na kole, určitě víte, že pro pohodlnou a kvalitní jízdu je potřeba mít takzvaně vycentrovaná kola. V opačném případě, kdy je například přední kolo nějakým způsobem pokřiveno, říkáme, že „hází“, což se projevuje chvěním řidítek a ztrátami vynaložené energie při jízdě.

Pokus: Podívejme se, jak  budou rotovat volně zavěšená tělesa, která nebudeme nutit k rotaci podél nějaké určité osy. Podrobnosti

Z výsledku pokusu je patrné, že volně rotující symetrické těleso rovnoměrně rotuje kolem osy, vůči které je symetrické. Takové ose procházející těžištěm tělesa se říká volná osa rotace. Odstředivá síla se přitom snaží vzdálit různé body tělesa co nejdále od osy otáčení, takže těleso bude rotovat kolem osy s největším momentem setrvačnosti J.

         To si lze snadno představit například u hranolu, který má tři navzájem kolmé osy symetrie, vůči kterým má momenty setrvačnosti J₁ < J₂ < J₃. Hlubší teoretický rozbor však ukazuje (a experimentálně se dá dokázat), že v tomto případě může těleso stabilně rotovat také kolem osy, vůči které má nejmenší moment setrvačnosti J₁. Rotace kolem osy určené J₂ je nestabilní.

?Kolem které osy budou rotovat jiná symetrická tělesa?

Pokud má těleso moment setrvačnosti vůči jedné ose symetrie největší a vůči jiným stejný  J₁ = J₂ < J₃ (například pravidelný čtyřboký hranol nebo válec), bude stabilně rotovat vůči ose s momentem setrvačnosti J₃. To znamená, že dlouhá tyčka bude rotovat kolem některé z os kolmých na osu válce, nízká kruhová destička naopak kolem osy kolmé na podstavu. Můžete si to vyzkoušet ještě jednou předchozím pokusem.

Těleso, které má moment setrvačnosti vůči všem osám symetrie stejný (například krychle nebo koule), bude volně rotovat kolem libovolné z těchto os.

Na obsah