Podivné chování míčků

Mluvili jsme o zákonu zachování energie při ideálně pružné srážce a o tom, že při reálné srážce se část deformační energie přemění na teplo, a že tedy například míč po odrazu od země nevyskočí do takové výšky, z jaké byl vypuštěn. Jak potom vysvětlíme následující pokus?

Pokus: Vezmeme si lehký a těžký míček (například pingpongový míček a „hopík“ – pružný míček z tvrdé gumy pro děti). Oba míčky podržíme v určité výšce nad stolem tak, že pingpongový míček leží na těžším gumovém míčku, a v této poloze pustíme míčky na stůl. Míčky musí dopadat na stůl kolmo na sobě.

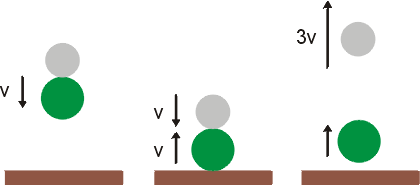
Pingpongový míček vyletí po odrazu do několikanásobně vyšší výšky, než z jaké byly oba míčky vypuštěny. 

? Není to v rozporu se zákonem zachování energie? 

A dokážeme určit do jaké výšky by měl pingpongový míček vyletět? Komentář

Na první otázku, jestli není při pokusu se dvěma míčky porušen zákon zachování energie, odpovíme, podíváme-li se ještě jednou podrobně na výsledek pokusu. Zákon zachování by byl porušen tehdy, kdyby nejenom lehký míček vyletěl výše než do své původní polohy, ale kdyby zároveň i spodní těžší míček vyletěl alespoň do stejné výšky, z jaké byl vypuštěn. Při pokusu však vidíme, že těžší míček vyskočí mnohem méně. Můžeme tedy předpokládat, že těžší míček předal při srážce část své energie lehčímu míčku, a zákon zachování energie je tak „zachráněn“.

         O tom, jak velké je množství energie předané mezi míčky, si řekneme později a zkusíme zatím odpovědět na druhou otázku - do jaké výšky vyletí pingpongový míček.

         Úloha se zjednoduší, budeme-li nejdříve uvažovat, že hmotnost pingpongového míčku je zanedbatelná vůči hmotnosti těžšího míčku a hmotnost obou míčků je zanedbatelná vůči stolu, na který dopadají. Potom totiž můžeme využít výsledků úlohy o rychlosti míče při jeho odkopu nohou. Víme, že celková velikost změny rychlosti míčku po odrazu od mnohem těžšího stolu je 2v, kde v je rychlost míčku před dopadem. Stejně i velikost změny rychlosti pingpongového míčku po odrazu od těžkého míčku je 2v, zde ovšem jde o změnu rychlosti ne vůči stolu, nýbrž vůči těžšímu míčku. Celková velikost změny rychlosti pingpongového míčku vůči stolu je tedy 4v a jestliže jeho rychlost těsně před srážkou měla velikost v a směr dolů, bude po srážce mířit nahoru a mít velikost 4v – v = 3v vůči stolu.

Výšku h, do které pingpongový míček vyletí, teď jednoduše určíme z rovnosti jeho kinetické energie těsně po odrazu a potenciální energie v místě maximální výšky.

Jestliže velikost rychlosti pingpongového míčku po odrazu je třikrát větší než před dopadem, měla by být výška, do které míček vyletí, devětkrát větší než výška, ze které byly míčky vypuštěny (výška výstupu závisí na rychlosti kvadraticky).

Skutečnou výšku do které pingpongový míček vyletí změříme jednoduše například tak, že vedle míčků podržíme kolmo ke stolu metr, míčky pustíme z výšky například 20 cm nad stolem a sledujeme, jak vysoko pingpongový míček vyletí. Zjistíme, že vyletí pouze do asi  čtyřnásobné výšky, podle toho, jaké míčky použijeme.

? Jak je možné, že se skutečná výška, do které míček vyletí, tolik liší od teoretického výsledku?

Bylo by zajímavé zjistit, čím je způsoben tento rozdíl, konkrétně, jak závisí změna rychlosti těles při srážce na materiálu těles a na jejich hmotnosti.

         Podobnými otázkami se zabýval v 17. století český učenec Jan Marcus Marci z Kronlandu (Lanškrouna), když studoval srážky koulí na tehdy vzácném kulečníku. Ve svém díle De proportione Motus (O úměrnosti pohybů) z roku 1639 poprvé rozlišil pružné a nepružné srážky a zformuloval též řadu zákonů týkajících se pružného rázu.

         Systematicky vyřešil úlohu o rázu koulí až v roce 1668 Ch. Huygens na podnět soutěže vypsané Královskou společností v Londýně.  

Na obsah