Část 1: Základy

I když se chceme zabývat relativitou, budeme muset nejdříve připomenout některé základní (a pro naše další úvahy důležité) pojmy z klasické (někdy také nazývané Newtonovy) mechaniky. Bez toho by se nám nová teorie „budovala“ jen těžko. Chceme-li totiž ukázat, jak teorie relativity změnila pohled fyziky na svět, není od věci si připomenout, jak se na svět díváme „klasicky“. Pro některé čtenáře může být začátek této kapitoly čistě opakováním, přesto je doporučeno alespoň její zběžné prohlédnutí. To, co si tu řekneme, patrně nebude na první pohled souviset s relativitou, ale opravdu jen na první pohled.

Se základy klasické mechaniky by měl být obeznámen každý, kdo si prošel fyzikou střední školy. I když se to některým studentům tak jevit nemusí, středoškolská mechanika je velmi přímočará. Pro člověka znamená většinou první setkání s matematickým popisem světa kolem nás, a tím pádem je důležitá nejen sama o sobě, ale zároveň nás učí, jak obecně řešit problémy i v jiných oblastech fyziky.

Mechanika se zabývá popisem mechanického pohybu, tedy přemisťováním různých předmětů v prostoru kolem nás. Způsobů, jak takový pohyb popsat, je celá řada. Protože ale chceme být jednoznační, musíme vždy stanovit, vůči čemu daný pohyb popisujeme. Proč je to důležité, si ukážeme na následujícím příkladu:

Představme si, že stojíme ve vlaku. Do zastávky je daleko, takže vlak jede stále stejně velkou rychlostí po rovných kolejích. V ruce držíme kámen, který v jednu chvíli pustíme na zem. Každý, komu někdy něco upadlo v takto rovnoměrně přímočaře jedoucím dopravním prostředku, jistě bude díky své zkušenosti souhlasit s tvrzením, že kámen poletí svisle dolů a dopadne na podlahu stejně, jako bychom stáli na pevné zemi (více si o tomto jevu povíme později, prozatím to berme jako vyzkoušený fakt). Zároveň v tu chvíli stojí náhodný kolemjdoucí venku u kolejí a pozoruje vlak. Otázka zní: Vnímá venku stojící pozorovatel pohyb kamene stejně jako my? A pokud ne, tak jak?

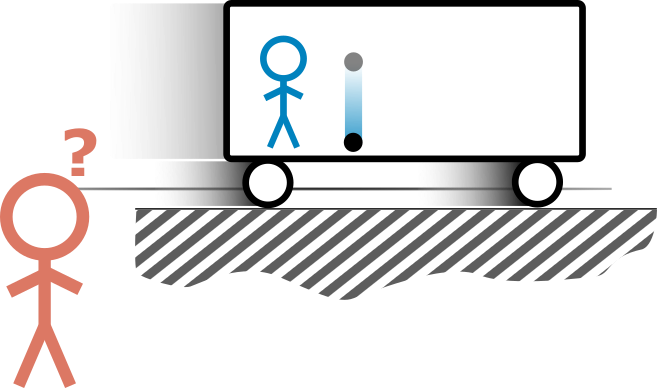
Obrázek 1.1

Musíme si uvědomit, že my se pohybujeme spolu s vlakem vůči pozorovateli venku, který je vzhledem k zemi a kolejím v klidu. Jestliže pro nás ve vlaku vykonává kámen jen pohyb směrem dolů, znamená to, že dopadne na podlahu přesně pod tím místem, z něhož jsme kámen pustili. Ale kámen padá nějakou konečnou dobu, po kterou vlak ujede kus cesty. Z pohledu venku stojícího pozorovatele tedy pustíme kámen z ruky nad určitým místem na kolejích a ten se dotkne podlahy vozu o kus dále, nad jinou částí kolejí. Osoba venku tedy určitě neuvidí pád přímo dolů. V čem je ten rozdíl? Jak my ve voze, tak člověk u kolejí vidíme pohyb dolů způsobený tíhovou silou Země. Venkovní pozorovatel ale ještě k tomu vnímá náš vodorovný pohyb po kolejích díky vlaku. Tuto tzv. vodorovnou složku rychlosti má i kámen, když ho držíme v ruce, a má ji i poté, co ho pustíme z ruky, protože kolem není nic, co by ho v tomto směru omezilo. Je to právě zachování stejného pohybu vpřed u kamene, které způsobí, že z našeho pohledu uvnitř vlaku padá jen směrem dolů. A konečně, ze střední školy víme, že předmět, který má nenulovou počáteční vodorovnou složku rychlosti a zároveň na něj působí tíhová síla, se bude pohybovat přibližně po parabole, dokud nenarazí na překážku nebo nedopadne na zem. Říká se tomu vodorovný vrh.

Obrázek 1.2 My ve vlaku vidíme, že kámen padá pouze svisle dolů, protože ve vodorovném směru vůči nám nemění polohu. Nicméně vůči pozorovateli venku se pohybuje i vodorovně, takže ve výsledku se vůči němu kámen pohybuje po parabole.

Vidíme, že to, k čemu vztahujeme pohyb pozorovaného předmětu, ovlivňuje náš popis situace. Nikdy nevidíme přímo rychlost daného tělesa. Pozorujeme pouze změnu polohy vztaženou k jinému zvolenému předmětu (velmi často nám samotným) za nějaký čas, a na základě toho pak vyvozujeme závěry. Pro popsání pohybu potřebujeme tedy vědět, jak se změnila poloha předmětu v prostoru v čase. Aby byl ale náš popis jednoznačný, musíme říci, vůči čemu polohu předmětu popisujeme. Potřebujeme tzv. vztažnou soustavu.

1.1 Vztažná soustava

Existuje nepřeberné množství vztažných soustav, ale pro všechny je společné, že pomocí několika číselných údajů popisují polohu libovolného bodu od pevně zvoleného místa (například střed fotbalového hřiště) nebo tělesa (strom, pouliční lampa, pozorovatel sám apod.). Když budeme například chtít popsat polohu bodu na nějaké dané přímce, musíme si pouze zvolit jeden konkrétní bod, od kterého budeme vzdálenost měřit. Takovému bodu se nejčastěji říká počátek. Dále potřebujeme umět měřit vzdálenost. K tomu musíme říci, co je to vzdálenost „jedna“. Nabízí se samozřejmě použít metr či příslušnou násobnou jednotku (milimetr, kilometr, nanometr, apod.). Stejně tak ale můžeme použít jako jednotku kus větve nebo délku našeho chodidla. Důležité je, abychom byli schopni vyjádřit vzdálenost každého bodu od počátku v násobcích naší jednotky, tedy přidělit jí tzv. souřadnici. Počátku se velmi často přiřazuje hodnota nula. Výhodou této volby je, že pak můžeme snadno rozlišovat body na jedné a druhé straně od počátku pomocí znaménka plus nebo mínus u souřadnice bodu.

Poznámka 1.1

Matematika pracuje se souřadnicemi bodu, jenže bod není reálný objekt, protože nemá žádné rozměry. Zkuste si udělat tužkou na papíře bod. Ať se budete snažit sebevíc, vždycky dostanete skvrnu konečného rozměru. Z dálky nám může připadat zanedbatelně malá, ale zblízka se už jako bod moc jevit nebude. A co teprve pod mikroskopem? I tu nejmenší tečku, kterou je člověk schopen vytvořit, tvoří nekonečně bodů. Proto si musíme při popisu reálných těles pomoci. Jednoduše si najdeme důležitá a snadno rozpoznatelná místa na daném předmětu, přiřadíme jim souřadnice a pak se díváme, jak se pohybují v čase. U tyče by nám tak mohly stačit začátek a konec. U předmětů pravidelného tvaru, u kterých se můžeme spolehnout na to, že svůj tvar ani velikost nebudou měnit (takovým předmětům říkáme ideálně tuhé) nám stačí jen několik málo důležitých bodů pro popsání celého pohybu. Pro sledování pohybu kulečníkové koule po plátně stačí většinou sledovat jen její střed, pokud nám je jedno, jak se točí. Kámen padající v tíhovém poli Země nahrazujeme pohybem jeho těžiště. Musíme mít ale na paměti, že to je v pořádku jen tehdy, když reálné rozměry kamene nehrají důležitou roli (vzpomínáte na pojem hmotný bod ze školy?). Složitější situace si žádají složitější modely a tím složitější řešení problému.

Pokud by nás zajímaly jen body na jedné přímce (například u auta jedoucího po rovné silnici), vystačíme jen s jednou souřadnicí. Pro popis bodů v rovině už ale potřebujeme souřadnice dvě. Nejčastějším, ale rozhodně ne jediným, způsobem je spojení dvou navzájem kolmých os, většinou je označujeme $x$ a $y$. Jsme tak v situaci notoricky známé každému středoškolákovi. Udáním dvou souřadnic libovolného bodu pak říkáme, v kterých místech na příslušných osách sestrojíme kolmice. Kolmice sestrojíme a ejhle, jejich průsečík je náš hledaný bod. V tomto případě jsou tedy souřadnice bodu vzdálenosti měřené na zvolených osách. Jak ještě uvidíme, existují i jiné než délkové souřadnice, souřadnicí může být například i úhel. Ale nepředbíhejme.

Zobecnění na trojrozměrný prostor, kde máme tři nezávislé směry, je již asi jasné. Místo dvou souřadnic máme tři a ke dvěma na sebe kolmým osám přidáme třetí. Námi sestrojená soustava souřadnic má výsadní místo na poli matematiky a fyziky. Říká se jí kartézská, na počest slavného francouzského učence René Descarta a je nejpoužívanějším typem soustavy souřadnic díky své relativní jednoduchosti. Pro použití takové souřadné soustavy nám stačí umět měřit vzdálenost, konstruovat pravé úhly a vhodně umístit počátek soustavy. Ať si představujeme, že náš počátek soustavy leží v rohu místnosti, uprostřed podlahy v autobusu nebo jsme jím my sami, vždy ho vztahujeme k určitému tělesu. Už náš první příklad s vlakem ukazuje, že vztažná soustava se může obecně pohybovat nějakou rychlostí (konstantní či proměnnou v čase). Dokonce se může i otáčet (např. člověk sedící na kolotoči apod.). Vždy ale platí, že abychom mohli jakýkoli pohyb tělesa a s ním spojené soustavy (například jedoucího vlaku) pozorovat, musíme ho vztáhnout k soustavě jiné (například spojené s kolejemi). Přecházení mezi různými souřadnými soustavami (tedy různými pohledy na situaci) je pro pochopení relativity zásadní, proto se mu budeme později hodně věnovat.

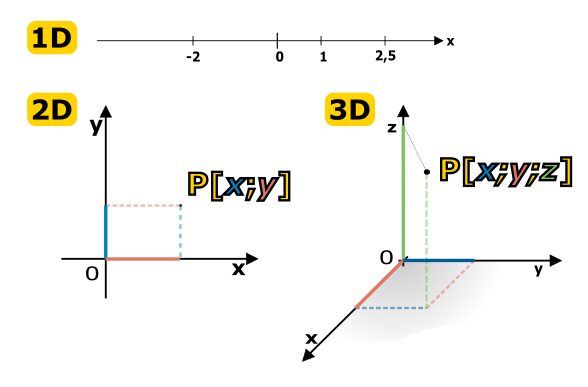
Obrázek 1.3 Vytvoření kartézské souřadné soustavy od jednoho prostorového rozměru až po všechny tři. Povšimněte si, že druhý z obrázků vypadá, jako bychom se na ten třetí dívali shora. To není náhoda. Orientace os na třetím obrázku je zvolena záměrně tak, aby tvořily tzv. pravotočivý systém (alternativou by byl levotočivý), což je obecně preferovaná varianta.

1.2 Čas v klasické mechanice

Pouhé udání polohy nějakého předmětu pro popis jeho pohybu jistě nestačí. Souřadnice jsou čísla a jejich udáním zafixujeme těleso na určitém místě, jako by se jednalo o fotografii. Stejně jako se film skládá z rychlého sledu jednotlivých fotografií, tak i my potřebujeme udat polohu sledovaného předmětu v po sobě jdoucích konkrétních okamžicích. Jinými slovy, chceme vědět, jak se poloha tělesa vyvíjí v čase. Jak to zjistíme? Například si můžeme zvolit určitý časový interval (řekněme třeba 5 sekund) a vždy po uplynutí tohoto času změříme a zapíšeme souřadnice předmětu v naší předem určené souřadné soustavě.

Takhle bude ale náš popis zjevně nespojitý (sekaný) a tomu opravdovému pohybu se bude podobat jen částečně. Chtěli bychom být přesnější, a tak musíme interval mezi měřeními zmenšit. Čím budou skoky mezi jednotlivými časy menší, tím přesnější bude náš popis (přesnější ve smyslu, že se bude více blížit skutečnosti). V principu můžeme, alespoň v našich úvahách, časový krok neomezeně zmenšovat až do chvíle, kdy se souřadnice stanou prakticky spojitou funkcí času. Opět si můžeme pomoci naší analogií s filmem. Budeme navyšovat počet po sobě jdoucích fotografií za sekundu, až jednotlivé snímky přestaneme vnímat a uvidíme již netrhaný pohyb typický pro film. Matematicky zdůrazňujeme závislost souřadnic na čase zápisem $x(t),y(t),z(t)$, kde $t$ je tradiční písmeno pro značení času. Abychom se ale nadále vyhnuli neustálému opisování téhož, dohodněme se, že, pokud nebude řečeno jinak, budeme od této chvíle chápat souřadnice bodu obecně závislé na čase a čas v závorce nebudeme explicitně vypisovat.

Jako fyzikální pozorovatelé a experimentátoři musíme tedy k popsání jakéhokoli pohybu využívat nejen souřadnice, ale i čas. Měření vzdálenosti nám koncepčně nedělá příliš problém, už jsme o něm navíc stručně mluvili. Podobná situace nastává u měření času. Opět si musíme definovat jednotku neboli jednotkový časový interval. Ve fyzice mu říkáme sekunda. Máme-li pak hodiny, které nám dokážou s využitím nějakého fyzikálního principu (kyvadlo, kmitání krystalu apod.) s dostatečnou přesností určit čas uplynulý od určitého okamžiku vyjádřený v násobcích naší zvolené jednotky (tedy určit, kolik sekund uplynulo od okamžiku, kterému říkáme nula), říkáme, že umíme měřit čas. Je zajímavé si uvědomit, že měření času prakticky znamená jen porovnání délky trvání námi zkoumaného jevu s délkou trvání jevu, na jehož principu fungují naše hodiny (např. kmit kyvadla).

Newtonovská mechanika přistupuje k pojmu času velmi intuitivně. Je těžké říci, co čas skutečně je, ale každý ho velmi dobře dokážeme prakticky využívat. Klasické představy o čase vycházejí z naší každodenní zkušenosti. Připadá nám samozřejmé, že čas plyne pro každého stejně nezávisle na tom, kde se nacházíme nebo jak rychle se pohybujeme. Nedělá nám sebemenší problém říci, že se nějaké dvě události staly zároveň (tj. ve stejném čase). Čas podle těchto představ hraje pouze roli kulisy, před kterou se všechno dění odehrává. Později ale uvidíme, že toto chápání nemusí vždy souhlasit s fyzikální realitou a že chování času může být daleko zajímavější, než bychom si mohli myslet. Tyto odchylky ale nastávají za podmínek, se kterými nemáme každodenní přímou zkušenost, a proto nám často připadají podivné a těžko přijatelné.

1.3 Fyzikální modely, ideální hodiny a měřící tyče

Na světě není nic ideální. My lidé nejsme dokonalí a ani věci, které vyrábíme, nejsou nikdy přesně takové, jaké bychom je chtěli. Problém je právě ve slově „přesně.“ Může například stůl měřit na délku přesně dva metry? Když ho přeměříme pásovým metrem, jehož nejmenší dílek je jeden milimetr, tak pravděpodobně naměříme skutečně dva metry. Co když ale vezmeme mikrometr? Nebo jiný přístroj, kterým jsme schopni měřit s přesností na setinu milimetru (deset mikrometrů, chcete-li)? Je nanejvýš pravděpodobné, že stůl, jehož délka je přesná v milimetrech, se pod přesnějším měřením ukáže být o trochu kratší nebo delší. Třeba jen v řádu mikrometrů, což je pro lidské oko naprosto nepostřehnutelné, ale přece. Můžete namítat, že tak malá nepřesnost není důležitá, že stůl plní svůj účel navzdory této skryté nedokonalosti, a budete mít samozřejmě pravdu. V praxi vždy vítězí dostatečná přesnost, protože je…no dostatečná.

Nám jde ale samozřejmě o princip věci. I kdyby si nějaký výrobce stolů dal takovou práci, aby jeho výrobek byl na mikrometr přesně dlouhý dva metry, můžeme svá měření dále zpřesňovat. Nastává tedy závod ve zpřesňování. Stolařova urputná snaha dosáhnout dokonalé přesnosti rozměrů stolu versus naše neoblomná touha ho vyvést z omylu. V tomto případě máme ale vítězství zaručeno, protože přesnost výroby má svůj limit. Všechny reálné předměty, takže i stoly, se skládají z atomů. Ty mají velikost řádově $10^{-10}$ metru. I kdyby zarputilý stolař sestavil svůj stůl pomocí obřího tunelovacího mikroskopu jeden atom po druhém, vyrovnal je k sobě nejlepším možným způsobem, my prostě jen zpřesníme své měření, zatímco on ke svému zklamání atomy menší neudělá. Nehledě na to, že všechny atomy vibrují díky své nenulové kinetické energii (která souvisí s teplotou látek), takže máme o důvod více, proč mluvit o absolutní přesnosti nemá moc cenu.

Pointou celé této myšlenkové konstrukce je, že nic na světě není absolutně přesné. Ať už měříme cokoli, vždy musíme počítat s nepřesností tohoto měření. Plány domů se nejčastěji navrhují v centimetrech (maximálně v milimetrech), protože to je přesnost, která zaručuje, že nám dům nespadne na hlavu. Stavět domy přesněji (to znamená používat přesněji tvarované cihly, všechno proměřovat daleko důkladněji apod.) by totiž byla nejspíš ztráta času a peněz. Většinou by to vlastně ani nešlo.

Nejen díky této „nedokonalosti“ reálného světa ve fyzice často idealizujeme. Ze střední školy dobře známe pojmy jako ideální plyn, ideální tekutina, ideální cívka apod. O všech těchto věcech víme a otevřeně přiznáváme, že na světě neexistují, přesto jsou pro nás důležité, protože napodobují chování určitých reálných jevů a svou nepřesnost vyvažují poměrnou jednoduchostí. Takovým nápodobám říkáme modely (často fyzikální modely, ale můžou být i matematické, sociologické, ekonomické, atd., prostě podle daného oboru zkoumání). Příroda je obecně velmi složitá a skrývá nepřeberné množství detailů, které člověk není schopen vnímat a pochopit všechny najednou. Modely nám pomáhají tím, že některé detaily ignorují nebo zanedbávají, abychom se mohli snadněji soustředit na to důležité. Vymyslet správný a věrohodný model není žádná legrace a spočívá v tom valná většina vědecké práce, ale když se to povede, jsme zase o krok blíž k pochopení té původní změti složitostí kolem nás.

V teorii relativity se hodně mluví o měření času a rozdílech v naměřeném čase. Ve všech následujících úvahách se předpokládá použití tzv. ideálních hodin. To znamená hodin, jejichž vnitřní konstrukce (ať už je jakákoli) nezpůsobuje, že by se předbíhaly nebo zpožďovaly. Jsou přesné a ať se s nimi děje cokoli (i kdyby třeba letěly rychlostí blízkou rychlosti světla), dá se spolehnout na jejich měření. O kolik složitější by byly jakékoli novátorské úvahy o prostoru a času, které relativita přináší, kdybychom se museli zároveň zabývat nedokonalostí našich měřících přístrojů. To patří k řemeslu experimentální fyziky. Teorie odhlíží od nedokonalostí krabiček, kterými se díváme na svět, a zabývá se světem samotným.

Podobně se mluví při měření vzdáleností o ideálních měřících tyčích, pomocí nichž měříme vzdálenost. Ideálních v tom smyslu, že nemění svoje rozměry s teplotou (v praxi považujeme reálné měřící tyče za přibližně ideální, pokud mění své rozměry méně, než jsme schopni měřit) nebo se jinak nedeformují z jiných důvodů, které by se daly odstranit (jiný, vhodnější materiál, jiná konstrukce apod.). V knihách se často můžeme dočíst o jakýchsi trojrozměrných lešeních sestavených z těchto tyčí, konstrukcích, pomocí nichž měříme vzdálenosti v naší souřadné soustavě a tím ji vlastně definujeme. Nemusíme se ale hned děsit, že by si fyzikové stavěli konstrukce ze speciálních trubek kamkoli přijdou, aby si dokázali něco změřit. Tahle poměrně vtipná představa je vlastně velmi praktickou metaforou, která říká, že umíme vždy měřit vzdálenosti ve všech třech rozměrech s dostatečnou přesností nehledě na to, jestli stojíme (samozřejmě vůči něčemu!) na místě nebo se naopak (opět vzhledem k něčemu) pohybujeme. Ačkoli opravdová měření by byla prováděna nějakým sofistikovanějším způsobem, i my budeme dále mluvit (či alespoň předpokládat existenci) o lešení z ideálních měřicích tyčí, protože nám tento model pomůže pochopit spoustu nového.

Je sice pravda, že takové hodiny a tyče v reálu zatím nikdo nevyrobil a ani nikdy nevyrobí, nicméně našim úvahám to není na obtíž. Prakticky to jen znamená, že se nezatěžujeme jejich nepřesností, která u všech sofistikovaných fyzikálních experimentů bývá velice malá a velmi dobře kontrolována. Místo toho se budeme při budování teorie soustředit na fyzikální jevy, které se nedají odstranit lepší konstrukcí hodin či měřících tyčí, a jsou proto zřejmě zakódovány do zákonů přírody jako takové. A to je právě to, co bychom chtěli poznat a pochopit.

1.4 Transformace souřadnic

Už víme, že je možné stejnou fyzikální situaci popisovat pomocí více systémů souřadnic a že mezi těmito systémy můžeme volně přecházet. Matematický nástroj, který nám tento přechod umožňuje, se nazývá transformace souřadnic. Je to v podstatě matematické vyjádření souřadnic jedné soustavy pomocí souřadnic soustavy druhé (a naopak). Ukažme si tento princip na konkrétním příkladu.

Posunutí soustavy

Dva kamarádi se rozhodli vykolíkovat obdélníkovou zahradu kvůli stavbě domu. K tomu musí každému kolíku přiřadit souřadnice vzhledem ke zvolenému počátku a zvoleným směrům jejich os. První z kamarádů se rozhodl měřit vše od prostředku zahrady, tam tedy zvolil počátek své soustavy souřadnic a určil si dvě na sebe kolmé osy $x$ a $y$. Druhému kamarádovi přišlo lepší zvolit jeden roh zahrady jako počátek a usnadnil si práci tím, že jako souřadné osy $x^\prime$ a $y^\prime$ použil plot. Oba způsoby jsou stejně správné, i když ten druhý možná o něco šikovnější. Otázka ale zní, jaký je vztah mezi souřadnicemi, které oba pánové naměří? Jinými slovy, jak vyjádříme jedny souřadnice jako funkce druhých a naopak?

Řekněme, že zahrada má obecně rozměry $42$ krát $34$ metrů (vizte obrázek níže). Jaké souřadnice má čárkovaný počátek v nečárkované soustavě (označme ji $S$ a na obrázku ji pro přehlednost vyznačíme zeleně)? Stejně tak se můžeme ptát opačně, jaké souřadnice má nečárkovaný počátek v čárkované soustavě $S^\prime$ vyznačené červeně?

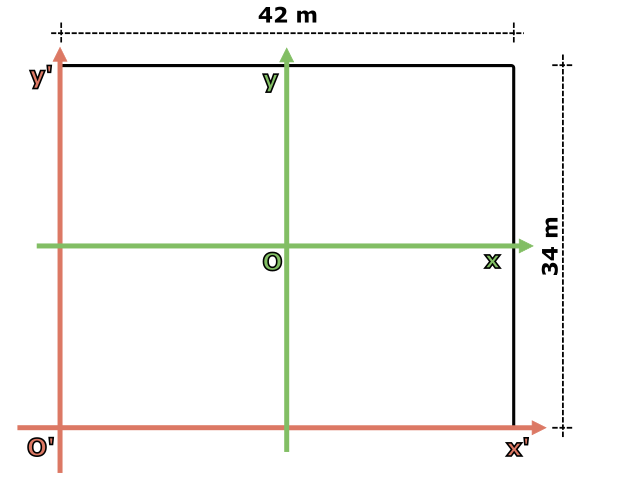
Obrázek 1.4 Dvě navzájem posunuté soustavy, nečárkovaná $S$ a čárkovaná $S^\prime$, a jejich počátky $O$ a $O^\prime$.

Kartézské souřadnice nějakého bodu jsou jeho vzdálenosti od počátku měřené kolmo na osy. Jestliže počátek čárkované soustavy, tedy bod $O^\prime$, je v levém dolním rohu zahrady, tak ve směru osy $x$ (tj. na obrázku vodorovně) je od prostředku vzdálen polovinu ze $42$ metrů, tedy $21\:\text{m}$ doleva. Protože levou část osy tradičně volíme jako zápornou, bude x-ová souřadnice $-21\:\text{m}$. Podobně ve směru osy $y$ je bod $O^\prime$ vzdálen $17\:\text{m}$ směrem dolů (opět v záporném směru), takže rovnou můžeme napsat souřadnice bodu $O^\prime$ v soustavě $S$, $S: O^\prime [-21\:\text{m};-17\:\text{m};0\:\text{m}]$. Kde se vzala ta nula na konci? To je hodnota z-ové souřadnice, tedy výška. Jestliže jsme si zvolili počátek v rovině země, standardně má tato rovina třetí souřadnici nulovou. Protože se zajímáme zatím jen o plochou zahradu, nemuseli bychom vlastně vůbec třetí souřadnici vypisovat. Chceme ale být pořádní a zvyknout si už rovnou na používání tří souřadnic, protože to budeme brzo potřebovat. Stejný bod můžeme vyjádřit i v čárkované soustavě, což je ještě jednodušší. Bod $O^\prime$ je počátkem $S^\prime$, proto v ní musí nutně mít souřadnice $S^\prime: O^\prime[0\:\text{m};0\:\text{m};0\:\text{m}]$ (pro přehlednost uvádíme u souřadnic bodu i danou soustavu, v případě, kdy bude z kontextu jasné, o kterou soustavu jde, budeme její označení u souřadnic vynechávat).

Stejným způsobem bychom mohli najít souřadnice bodu O v čárkované soustavě, dostáváme $S^\prime: O[21\:\text{m};17\:\text{m};0\:\text{m}]$, a z definice $S: O[0\:\text{m};0\:\text{m};0\:\text{m}]$. Nás by ale víc zajímalo, jak vyjádřit souřadnice jiných bodů než počátků. Ideálně bychom chtěli vzorec, který nám umožní spočítat souřadnice bodu v jedné soustavě, když známe jeho souřadnice v jiné. V tomto případě bychom měli na takový vzorec celkem snadno přijít.

Na obrázku níže máme body $K$ a $L$, které reprezentují kolíky zabodnuté v zemi. První z kamarádů, který měří od prostředku (a kterému jsme přiřadili nečárkovanou soustavu $S$), si naměřil vzdálenosti ke svým osám a určil tak souřadnice bodů $K[-2\:\text{m};-5\:\text{m};0\:\text{m}]$ a $L[6\:\text{m};4\:\text{m};0\:\text{m}]$. Druhému kamarádu se vzdálenosti nechce měřit, tak radši využije měření svého kolegy. Uvažuje následovně:

Podle první nečárkované souřadnice bodu $L$ vím, že je ve směru osy $x$ vzdálen $6\:\text{m}$ od počátku středové (nečárkované) soustavy a ten je vzdálen ještě $21\:\text{m}$ ve směru mé osy $x^\prime$ od mého počátku. Celkem je tedy bod $L$ ve směru $x^\prime$ vzdálen o $6\:\text{m}+21\:\text{m}=27\:\text{m}$.

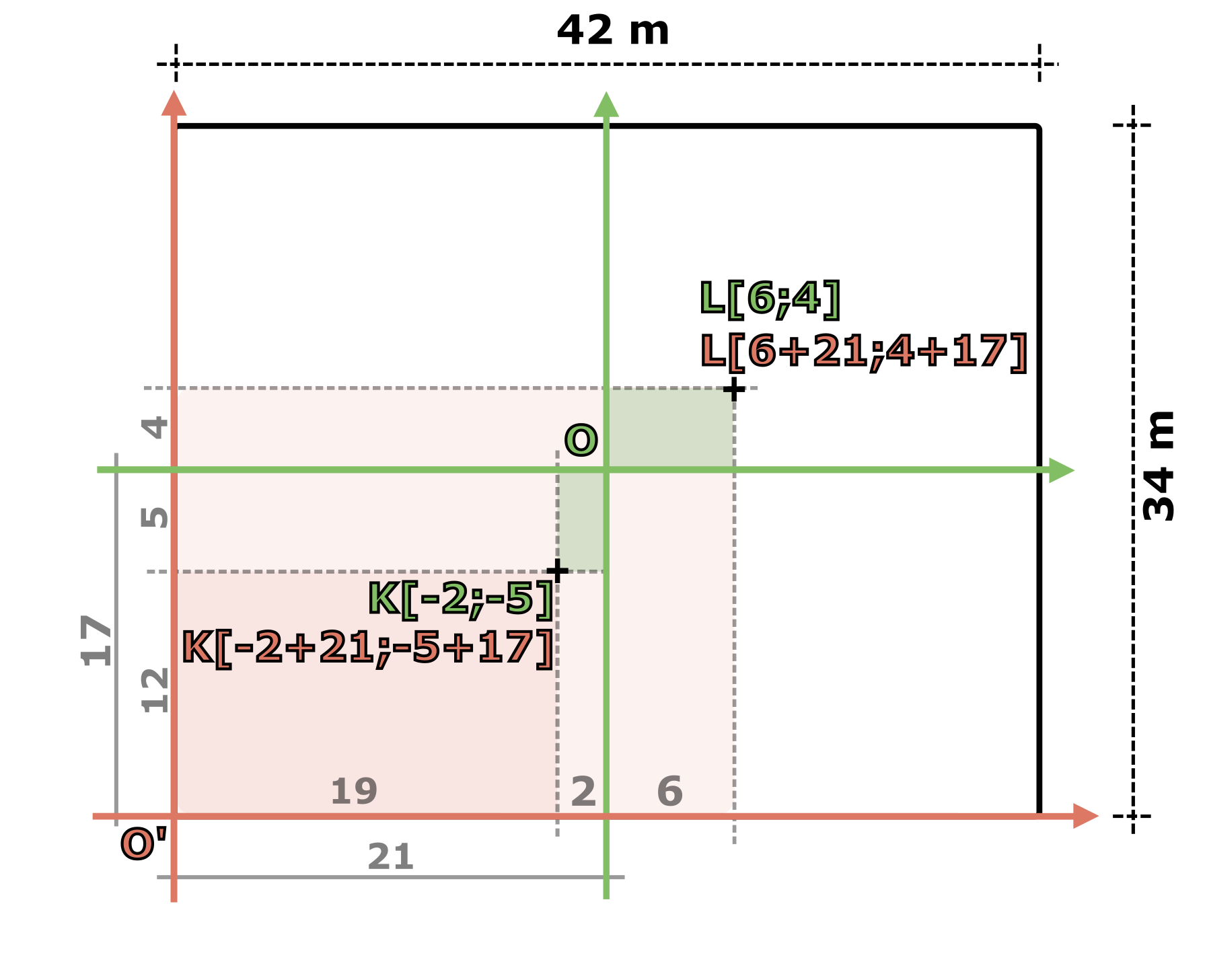
Obrázek 1.5 Detailní, byť trochu technický, popis využívání dvou vůči sobě posunutých systémů souřadnic v rovině $z=0$.

Stejná úvaha ale platí pro jakýkoli jiný bod, a protože by rád spočítal i souřadnice dalších bodů, zapíše si obecně: $$x^\prime=x+21 ,$$

což chápeme jako „x-ová souřadnice (libovolného bodu) v čárkované soustavě je rovna souřadnici $x$ v nečárkované soustavě plus $21$ (x-ová souřadnice nečárkovaného počátku - jednotku, tj. metry, můžeme zatím pro přehlednost vynechat). Snad si vzájemně ušetříme trochu námahy, když budeme místo toho říkat čárkované souřadnice a nečárkované souřadnice. Jen mějme na paměti, že se toto rozlišení týká soustav, ve kterých měříme.

Podobně bude druhý z kamarádů postupovat i se souřadnicí $y$. K původní nečárkované souřadnici musí přičíst ještě $17$, protože je jeho počátek ve směru $y^\prime$ právě o tolik více vzdálen od prostředku. Pro úplnost si ještě uvědomí, že oba pracují ve stejné výšce nad zemí (přesněji řečeno na zemi), a tak jsou jejich z-ové souřadnice stejné.

Spokojen se svou úvahou si může zapsat celou transformaci souřadnic z nečárkované soustavy do čárkované: \begin{align*} x^\prime &=x+21 \\ y^\prime &=y+17 \label{1.1}\tag{1.1}\\ z^\prime &=z . \end{align*}

Tento přístup, kdy jeden z pracantů všechno odměří a druhý si jen dopočítá, co potřebuje, se ale nezdá být moc fér. Místo toho by bylo lepší najít i obrácený přechod, z čárkované do nečárkované soustavy, aby oba mohli měřit různé části pozemku a následně si během pauzy přepočítat chybějící souřadnice toho druhého. Zastánce nečárkované soustavy by mohl samozřejmě postupovat velmi podobně jako jeho kolega a odvodit transformaci z obrázku výše. Může být ale chytřejší a uvědomit si, že mu stačí vyjádřit své nečárkované souřadnice ze sady rovnic \eqref{1.1} výše. Jednoduchou manipulací s rovnicemi dostává \begin{align*} x^\prime-21 &=x \\ y^\prime-17 &=y \tag{1.2}\\ z^\prime &=z . \end{align*}

Nakonec, protože je zvykem to, co chceme vypočítat, dávat většinou nalevo, tak jen prohodí levou a pravou stranu rovnic: \begin{align*} x &=x^\prime-21 \\ y &=y^\prime-17 \tag{1.3} \\ z &=z^\prime . \end{align*}

Ačkoli je náš příklad jednoduchý a přehledný, ukazuje nám něco obecně platného. Kdykoli popisujeme nějakou situaci v různých vztažných soustavách (zkráceně, i když ne úplně správně řečeno v různých souřadnicích), vždy existuje způsob, jak přepočítat souřadnice daných bodů v jedné soustavě do soustavy druhé či naopak. Technicky řečeno transformujeme souřadnice z jedné soustavy do druhé. Opět trochu zkráceně také říkáme, že mezi soustavami přecházíme.

Různé úhly pohledu na stejnou věc

Používání různých souřadných soustav je matematický postup, který může mít svoje výhody, ale neměli bychom nikdy zapomínat, že se tím nemění fyzikální podstata toho, co pozorujeme. Když přejdou pánové měřiči z červené souřadné soustavy do zelené, změní se souřadnice kolíků (bodů), ale to neznamená, že by se kolíky jako takové někam přemístili. Nevytrhnou se ze země či nevyryjí brázdu ve snaze přizpůsobit se našemu matematickému popisu. Souřadnice bodů jsou tedy relativní v pravém smyslu slova, mění se podle toho, odkud a v jakých směrech měříme, neboli vůči jaké vztažné soustavě jsme je zavedli.

Další důležitá otázka zní: změní se vzájemná vzdálenost bodů přechodem do jiné souřadné soustavy? Určení vzdálenosti dvou bodů z jejich souřadnic je na střední škole běžná věc. Stačí k ní obrázek 1.6 níže a Pythagorova věta. Připomeňme souřadnice bodů v nečárkované (středové) soustavě: $K[-2;-5;0]$ a $L[6;4;0]$. Oba body leží v jedné rovině, takže podle Pythagorovy věty s použitím souřadnic platí pro vzdálenost mezi body $K$ a $L$ (značíme většinou $|KL|)$: \begin{align*} |KL|^2 &=(x_L-x_K )^2+(y_L-y_K )^2 \\ &\\ |KL| &=\sqrt{(x_L-x_K )^2+(y_L-y_K )^2} . \end{align*}

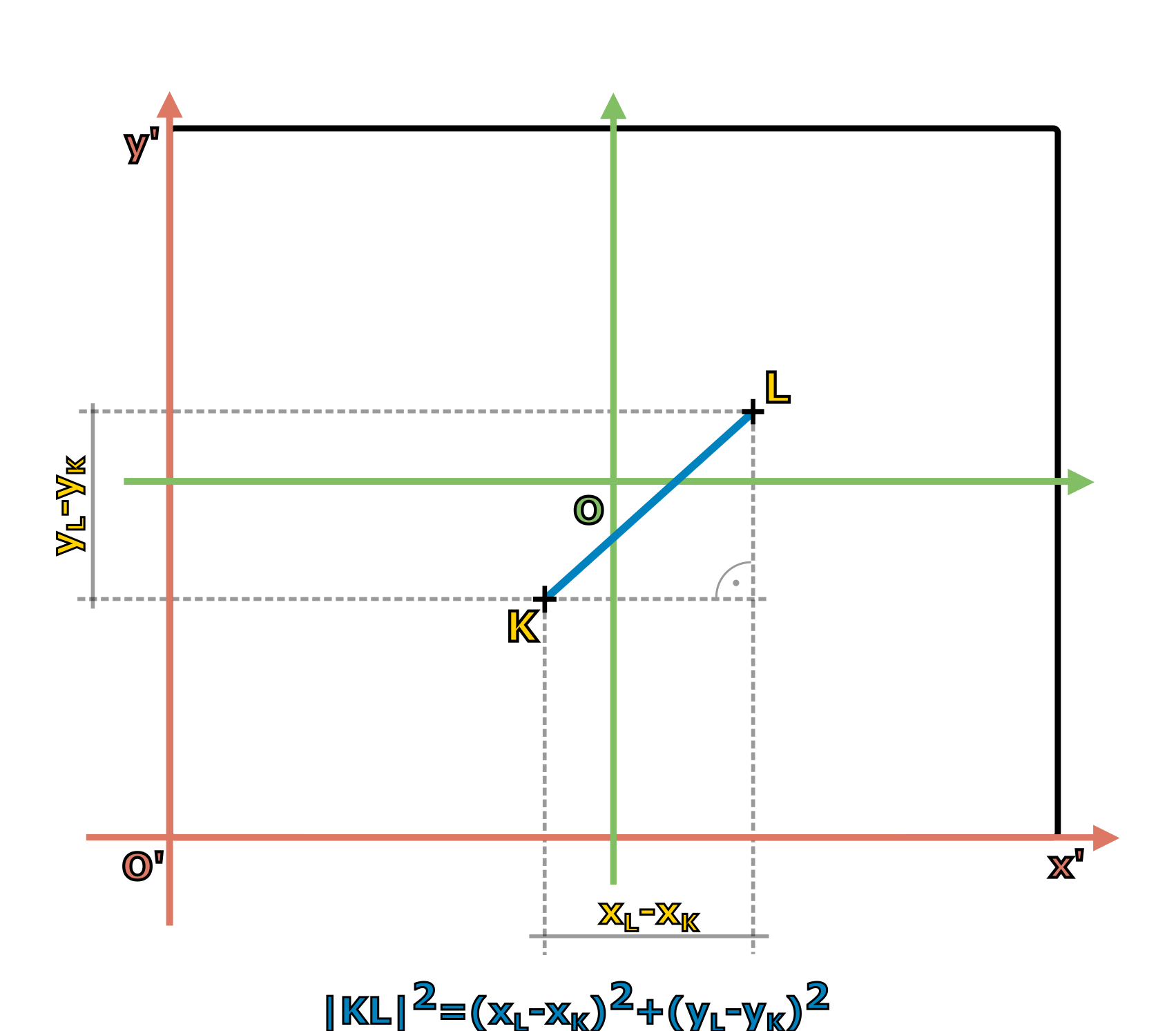
Obrázek 1.6 Výpočet vzdálenosti dvou bodů pomocí rozdílů souřadnic a Pythagorovy věty.

Dolní index tady používáme jako označení bodu, ke kterému souřadnice patří. Matematicky by řešením rovnice samozřejmě byla i odmocnina se znaménkem mínus, ale protože vzdálenost musí být vždycky kladná, toto řešení nás nezajímá. Po dosazení dostáváme \begin{align*} |KL| &=\sqrt{(6-(-2))^2+(4-(-5))^2} \\ &=\sqrt{8^2+9^2}=\sqrt{145}. \end{align*}

Ne příliš kulaté číslo, ale taky je to číslo.

Zkusme teď stejný proces pro čárkovanou soustavu. Z transformace \eqref{1.1} nebo obrázku 1.5 vidíme, že čárkované souřadnice bodů jsou $S^\prime:K[19;12;0]$ a $S^\prime:L[27;21;0]$. Po dosazení dostáváme \begin{align*} |KL| &=\sqrt{(x_L^\prime-x_K^\prime)^2+(y_L^\prime-y_K^\prime)^2} \\ &= \sqrt{(27-19)^2+(21-12)^2}=\sqrt{(8)^2+(9)^2}=\sqrt{145}. \end{align*} Snad nás nepřekvapí, že vyšlo stejné číslo. Už jsme si rozmysleli, že vzdálenost bodů na použitých souřadnicích nemůže záviset. Naše tvrzení můžeme dokázat i obecně: \begin{align*} |KL| &=\sqrt{[x_L+21-(x_K+21)]^2+[y_L+17-(y_K+17)]^2} \\ &=\sqrt{[x_L-x_K]^2+[y_L-y_K]^2}=...=\sqrt{145} . \end{align*}

Ve výpočtu jsme vlastně jen použili transformaci souřadnic \eqref{1.1}. Jestliže se tedy nezmění reálné místo zatlučení kolíků v zemi, nemůžou se změnit ani jejich vzájemné vzdálenosti. Říkáme, že vzdálenost bodů je při transformaci souřadnic invariantní (neměnná).

Při počítání vzdálenosti bodů $K$ a $L$ jsme nehezky vynechali třetí souřadnice bodů. V tomto speciálním případě (oba body stejně vysoko) jsme tím chybu neudělali, ale obecně bychom nedostali správný výsledek. Svět, ve kterém žijeme je trojrozměrný, a proto bychom měli umět počítat vzdálenost bodů, které jsou libovolně v prostoru umístěny. K tomu nám slouží zobecněná, či chcete-li trojrozměrná Pythagorova věta. Ta jednoduše vychází z té původní plošné verze (kterou má každý vrytou do paměti jako $c^2=a^2+b^2)$ a pouze přidává do výpočtu z-ové souřadnice: $$|KL|^2=(x_K-x_L)^2+(y_K-y_L)^2+(z_K-z_L)^2.$$

Odvození trojrozměrné verze Pythagorovy věty není těžké, ale nechceme s ním tady překážet. Můžete si ho vyzkoušet sami jako cvičení na konci kapitoly.

Tento příklad mluví o vzdálenosti konkrétních bodů $K[x_K;y_K;z_K]$ a $L[x_L;y_L;z_L]$. Rádi bychom ale nějaký obecnější zápis, který se neopírá o jména konkrétních bodů, a my bychom tak měli možnost volby. Označme rozdíly souřadnic pomocí řeckého písmene velké delta $\Delta$ (ve fyzice často označuje změnu nebo rozdíl) $$\Delta{}x=x_K-x_L, \Delta{}y=y_K-y_L, \Delta{}z=z_K-z_L,$$

a vzdálenost libovolných dvou bodů potom $\Delta{}s$. Nyní můžeme zapsat zobecněnou Pythagorovu větu \begin{equation}\label{3DPyth} (\Delta{}s)^2=(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2 \tag{1.4}. \end{equation}

Shrnutí první části

Popis pohybu je relativní v tom smyslu, že pozorovatelé v různých vztažných soustavách ho vnímají každý jinak. Způsob, jakým daný jev pozorujeme, nemá na jeho průběh ale žádný reálný vliv.
Základem každého měření je určení jednotky (délka 1 metru, doba 1 sekundy, hmotnost 1 kilogramu, elektrický proud 1 ampéru atd.) a pak vyjádření naměřené veličiny v násobcích této jednotky ($89{,}5\enspace\mathrm{kg},$ $12\enspace\mathrm{s},$ $10\enspace\mathrm{A}, ...)$.
Teorie relativity mluví o měření vzdálenosti pomocí ideálních měřících tyčí a času pomocí ideálních hodin. Je to celkem užitečný koncept, který mimo jiné znamená, že v teoretických úvahách odhlížíme od nepřesností způsobených reálným měřením. (To neznamená, že bychom na ně zapomněli, při skutečných experimentech s nimi fyzici samozřejmě počítají velice pečlivě.)
Polohu reálných objektů matematicky popisujeme pomocí bodů a jejich souřadnic v daném souřadném systému (například kartézský systém $x,y,z)$. Polohu bodu můžeme vyjádřit pomocí různých druhů souřadnic a jejich soustav, nemění se tím ale fyzikální podstata situace. Například fyzická vzdálenost bodů je při transformaci souřadnic stále stejná. Je vůči ní invariantní.
V trojrozměrném prostoru platí pro vzdálenost bodů $\Delta s$ zobecněná Pythagorova věta: $$(\Delta{}s)^2=(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2$$

Příklady k první části

Zobecněná Pythagorova věta snadno a rychle

S pomocí obrázku níže dokažte platnost vzorce \eqref{3DPyth}. Nápovědu si můžete rozkliknout níže.

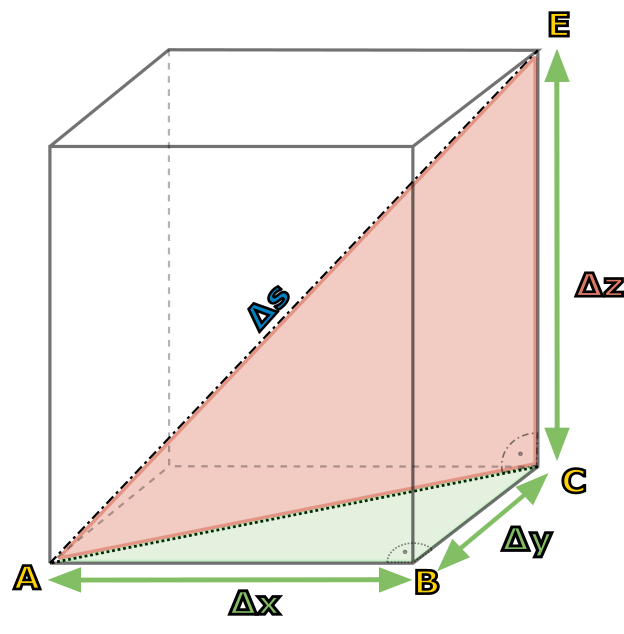
Obrázek 1.7 Odvození trojrozměrné Pythagorovy věty.

Odvození třírozměrné Pythagorovy věty

Rozepište dvourozměrnou Pythagorovu větu pro trojúhelník $ABC$.

Podobně postupujte v případě trojúhelníku $ACE$, dosaďte z první rovnice $|AC|^2$.

Pokud jste obdrželi rovnici \eqref{3DPyth}, pochvalte se za dobře vykonanou práci.

Vypočítejte vzdálenosti bodů zadaných souřadnicemi: \begin{align*} a)~&A[4;-2;1],~B[-3;7;6] \\ b)~&K[1;2;3],~L[-3;-2;-1] \\ c)~&P[9;1;1],~Q[-2;7;-5] \\ d)~&X[0;4;-7],~Y[7;12;2] \end{align*}

Pythagoras na kolotoči

Další možnou a přitom elementární transformací souřadné soustavy je rotace kolem osy. Na obrázku níže máme příklad takové rotace kolem osy $z$ o obecný úhel $\alpha$. Tímto způsobem otočíme souřadné osy $x$ a $y$ o úhel $\alpha$, čímž vytvoříme čárkované osy $x^\prime$ a $y^\prime$, a následně přiřadíme každému bodu o původních $(x,y,z)$ nové hodnoty souřadnic $(x^\prime,y^\prime,z^\prime)$ podle níže uvedených rovnic. Je logické, že se souřadnice $z$ nemění, stejně jako se nemění výška určitého bodu na točícím se kolotoči.

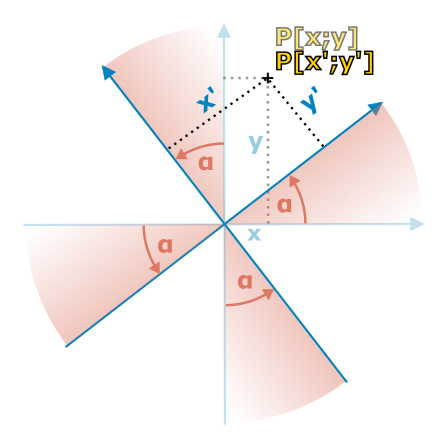
Obrázek 1.8 Rotace kolem osy $z$ o úhel $\alpha$ (pohled ze shora ve směru osy). Při ní zůstávají body ve stejné „výšce,“ takže $z^\prime=z$.

Speciálním případem rotace je otočení o $90°$. Při ní se prohodí osy, ale s opačným znaménkem u druhé souřadnice (viz obrázek). Transformace tedy nutně vypadá následovně: \begin{align*} x^\prime&=y \\ y^\prime&=-x \label{rot}\tag{1.5} \\ z^\prime&=z . \end{align*}

Ověřte, že v tomto speciálním případě platí \begin{align*} |AB|^2&=(x_B-x_A )^2+(y_B-y_A )^2+(z_B-z_A )^2 \\ &=(x^\prime_B-x^\prime_A )^2+(y^\prime_B-y^\prime_A )^2+(z^\prime_B-z^\prime_A )^2 \end{align*}

pomocí výše popsané transformace \eqref{rot} (nezapomeňte, že transformace platí pro každý bod zvlášť, tedy například $x_B^\prime=y_B$ a $x_A^\prime=y_A)$.

Pro libovolný úhel $\alpha$ vypadá rotace kolem osy $z$ takto: \begin{align*} x^\prime&=x.\cos{\alpha}⁡+ y.\sin⁡{\alpha} \\ y^\prime&=-x.\sin⁡{\alpha}+y.\cos⁡{\alpha}\label{rot2} \tag{1.6}\\ z^\prime&=z . \end{align*}
1. Ověřte, že pro úhel 90° přejdou tyto obecné rovnice na případ transformace \eqref{rot}.
2. Napište transformace souřadnic při rotaci kolem osy $z$ o $45°$, $180°$, $225°$, $270°$ a $360°$.
3. Lze ukázat, i když poněkud zdlouhavě, že i v případě obecné rotace souřadnic kolem osy se vzdálenost dvou libovolných bodů zachovává. Můžete si to zkusit rovnou sami nebo se můžete inspirovat řešením níže.

Řešení

Stačí do transformace \eqref{rot2} dosadit $\alpha=90°$. Jelikož $\sin{90°}=1$ a $\cos{90°}=0$, dostáváme ihned hledanou transformaci \eqref{rot}.

Opět se jedná pouze o dosazení za úhel otočení a vyčíslení funkcí sinus a kosinus. Mělo by nám vycházet: \begin{array}{c|c|c|c|c} \alpha=45° & \alpha=180° & \alpha=225° & \alpha=270° & \alpha=360° \\ \hline x^\prime=\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y & x^\prime=-x & x^\prime=-\frac{\sqrt{2}}{2}x-\frac{\sqrt{2}}{2}y & x^\prime=-y & x^\prime=x \\ y^\prime=-\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y & y^\prime=-y & y^\prime=\frac{\sqrt{2}}{2}x-\frac{\sqrt{2}}{2}y & y^\prime=x & y^\prime=y \\ \end{array}
V tabulce jsme pro přehlednost vynechali třetí souřadnice, protože se rotací kolem osy $z$ nemění. Některé naše výpočty se dají ověřit na první pohled. Například nás určitě nepřekvapí, že otočení soustavy o $180 °$ obrátí znaménko obou souřadnic, a otočení o $360 °$ situaci nijak nezmění.

To, že bodům přiřadíme jiné souřadnice, nijak neovlivňuje jejich reálnou polohu. Zdá se být tedy celkem přirozeným požadavkem, aby se vzdálenosti libovolných bodů od sebe rotací nezměnily. Nyní ověříme, že naše transformace souřadnic tuto vlastnost opravdu má.

Vyberme si libovolné dva body $P$ a $Q$ v rovině $xy$ a označme jejich vzdálenost $\Delta{}s$. Pythagorova věta nám říká, že pro vzdálenost bodů platí: \begin{equation*} (\Delta{}s)^2=(x_Q-x_P )^2+(y_Q-y_P )^2=(\Delta{}x)^2+(\Delta{}y)^2 , \end{equation*} a stejně tak v čárkované soustavě: \begin{equation*} (\Delta{}s^\prime)^2=(x_Q^\prime-x_P^\prime)^2+(y_Q^\prime-y_P^\prime)^2=(\Delta{}x^\prime)^2+(\Delta{}y^\prime)^2. \end{equation*}

Chceme ukázat, že $\Delta{}s=\Delta{}s^\prime$. Protože vzdálenost je vždycky kladná veličina, stačí nám ukázat, že se rovnají druhé mocniny. K tomu si můžeme všimnout, že transformační vztahy výše platí i pro přírůstky souřadnic: \begin{align*} \Delta{}x^\prime&=x_Q^\prime-x_P^\prime=x_Q\cos⁡{\alpha}+ y_Q\sin⁡{\alpha}-x_P\cos{\alpha}-y_P\sin{\alpha} \\ &=(x_Q-x_P)\cos{\alpha}+(y_Q-y_P)\sin{\alpha}=\Delta{}x \cos⁡{\alpha}+\Delta{}y \sin⁡{\alpha} \\ \Delta{}y^\prime&=y_Q^\prime-y_P^\prime=-x_Q\sin⁡{\alpha}+y_Q\cos{\alpha}+x_P\sin⁡{\alpha}⁡-y_P\cos{\alpha} \\ &=-(x_Q-x_P)\sin{\alpha}+(y_Q-y_P)\cos{\alpha}=-\Delta{}x \sin⁡{\alpha}+\Delta{}y\cos⁡{\alpha} . \end{align*} Tyto přírůstky nakonec dosadíme do rovnice pro kvadrát čárkované vzdálenosti: \begin{align*} (Δs^\prime)^2&=(Δx^\prime)^2+(Δy^\prime)^2=(Δx\cos⁡{\alpha}+Δy\sin⁡{\alpha})^2+(-Δx\sin⁡{\alpha}⁡+Δy\cos{\alpha})^2 \\ &=(Δx)^2[\cos^2{\alpha}+\sin^2⁡{\alpha}]+2ΔxΔy\sin{\alpha}\cos{\alpha}+(Δy)^2[\sin^2⁡{\alpha}+ \cos^2⁡{\alpha}]-2ΔxΔy\sin⁡{\alpha}\cos⁡{\alpha} \\ &=(Δx)^2+(Δy)^2=(Δs)^2 \end{align*} Tím je náš důkaz přímým výpočtem hotov.