4.3 Schwarzschildův prostoročas
Nejdůležitější závěr předcházející kapitoly byl, že chceme-li konkrétně popsat a následně pracovat s gravitací jako zakřiveným prostoročasem, potřebujeme znát odpovídající metriku. K jejímu nalezení slouží tzv. Einsteinovy rovnice (ER, někdy se také používá Einsteinovy polní rovnice nebo Einstenův gravitační zákon), které už ale svou složitostí překračují naše momentální možnosti a zájemce si o nich může detailnější informace zjistit jistě sám. Ale i když je řešení této soustavy rovnic matematicky komplikované, její základní filozofie je vcelku jednoduchá. Je názorné představit si rovnice jako stroj. V tomto případě je vstupem matematický popis rozložení hmoty, energie a dalších přidružených veličin v prostoru, a výstupem je pak metrika daného prostoročasu (nebo aspoň jeho části). Stručně řečeno: „Řekni mi, jak je rozložena hmota (atd.), a já ti řeknu, jak se zakřiví prostoročas kolem“.
To se sice snadno řekne, ale hůře reálně udělá. ER jsou natolik komplikované, že dodnes existuje jen několik jejich přesných řešení, tj. několik konkrétních fyzikálních situací, kdy jsme schopni dopočítat se výsledného zakřivení prostoročasu. My se tedy nebudeme pouštět do komplikovaného matematického řešení, ale místo toho si vypůjčíme a rozebereme nejjednodušší a přitom pro naše pochopení nejdůležitější situaci, tzv. Schwarzschildovo řešení (čistě technicky vzato je nejjednodušším řešením Einsteinových rovnic plochý prostoročas, tj. tehdy když v okolí nejsou žádné gravitující zdroje, ale tato situace pro nás není teď zajímavá). Karl Schwarzschild byl německý fyzik a astronom, který v roce 1916, krátce po Einsteinově uveřejnění finální podoby jeho polních rovnic, jako první přišel s jejich přesným řešením (je zajímavé, že k tomu objevu přišel na válečné frontě, protože tehdy zuřila první světová válka a Schwarzschild sloužil jako poručík u dělostřelectva a prováděl výpočty balistických křivek). Ke svému řešení došel za jistých zjednodušujících podmínek, totiž že gravitující těleso je sféricky symetrické a nerotuje.
Je vhodné si hned rozmyslet, o jak velké zjednodušení se jedná. V našem povídání budeme často Schwarzschildovo řešení aplikovat na nám známá vesmírná tělesa jako je Země a Slunce, i když je běžně známo, že obě tělesa nejsou zcela přesně kulová a rotují kolem své osy. Když se ale například podíváme na Zemi, najdeme, že její rovníkový poloměr je přibližně \(6378\:\text{km}\) a polární přibližně \(6357\:\text{km}\). Člověku se tento rozdíl cca \(21\:\text{km}\) může zdát velký, ale musíme si uvědomit, že v porovnání s velikostí planety je to opravdu málo. Vezmeme-li rovníkový poloměr jako výchozí, pak je Země na pólech zploštělá jen o přibližně \(0{,}3\:\%\) této hodnoty. Pokud bychom si to představili na bowlingové kouli o průměru zhruba \(22\:\text{cm}\), znamená to, že koule by mohla být v jednom směru zploštělá o zhruba \(0{,}7\:\text{mm}\). To jistě není něco, co bychom dokázali od oka poznat, a bowlingovou kouli bychom považovali za skutečnou kouli. Stejně tak je i naše planeta natolik podobná kouli, že se k ní tak můžeme v dobrém přiblížení chovat (což už vlastně po celou dobu tohoto textu děláme). Podobný argument bychom mohli vyslovit i pro Slunce, jehož poloměr na rovníku a na pólu se liší o pouhých \(0{,}0009\:\%\).
Rotaci jistě Zemi upřít nemůžeme. Umíme dokonce i spočítat, jak rychle rotuje. Pomocí známého vzorečku pro obvodovou rychlost při kruhovém pohybu \(v=2\pi R_\text{Z}/T_\text{Z}\) můžeme pomocí rovníkového poloměru Země \(R_\text{Z}\) a periody otáčení \(T_\text{Z}\) (přibližně \(24\) hodin) spočítat rychlost, se kterou se s námi Země otáčí, když stojíme na rovníku (tam je tato rychlost otáčení největší, směrem k pólům se zmenšuje). Vyjde nám \(v\:\dot{=} \:464\:\text{m}/\text{s}\). To se samozřejmě zdá být poměrně velká rychlost v lidském měřítku, ale vzpomeňme si na speciální relativitu. Tam jsme viděli, že jelikož v porovnání s rychlostí světla (přibližně \(300 000\:\text{km}/\text{s}\)) je tato rychlost zanedbatelně malá, běžně při ní efekty speciální relativity nepozorujeme (vzpomeňte na tabulku 3.1). Zde je to podobné. Existuje totiž i řešení Einsteinových polních rovnic pro případ rotujícího tělesa, tzv. Kerrovo řešení, ale to už spadá opravdu mimo rámec možností tohoto textu. Už jen to, že bylo objeveno až \(47\) let po tom Schwarzschildově, značí, že se jedná o poměrně komplikovanou záležitost. Podstatné ale je, že Kerrovo řešení pro nulovou (či zanedbatelně malou) rotaci daného tělesa přechází v to Schwarzschildovo. Otázkou samozřejmě je, co to přesně znamená zanedbatelně pomalá rotace. Pro konkrétní vysvětlení bychom ale už příliš museli zabíhat do popisu Kerrova řešení. Zájemci se tedy mohou více dozvědět například na Wikipedii. My se dále přidržíme zjednodušení, kdy na Zemi, Slunce a podobná tělesa budeme aplikovat Schwarzschildovo řešení.
Poznámka 4.8
Rotace gravitujícího objektu s sebou nese zajímavé efekty jako např. tzv. strhávání vztažných soustav (frame-dragging). V tuto chvíli není v našich silách se takovou situací zabývat, ale alespoň poznamenejme, že existují experimenty, které již podobné efekty v okolí Země změřily, např. Gravity Probe B.
Schwarzschildova metrika
Ještě než se podíváme na Schwarzschildovu metriku, připomeňme si ještě jedno příjemné zjednodušení. V předchozí kapitole jsme se zmiňovali o tom, že jak v klasické mechanice, tak v relativitě platí, že pokud je zdroj gravitace sféricky symetrický (což je situace, které se teď budeme věnovat), bude se pohyb libovolného obíhajícího tělesa odehrávat pouze v jedné rovině. To by se samozřejmě správně mělo odvodit matematicky, ale my opět vystačíme s jednoduchou představou. Připomeňme si, jak to bylo. Představte si třeba satelit obíhající kulovou planetu. Dráha satelitu je stáčena gravitací, ale ta působí ve směru pomyslné spojnice satelitu a planety. Pokud tedy satelit vypustíme například v rovině rovníku, bude „zatáčet“ vždy směrem k planetě a nemá důvod uhnout ani nad severní ani nad jižní polokouli. Obíhá tedy stále ve stejné rovině. Podobná úvaha bude platit, i když satelit vypustíme jiným směrem než ve směru rovníku. Stále bude obíhat v jedné rovině (obrázek 4.36 nahoře) určené počáteční rychlostí tělesa a jeho spojnicí se středem planety. Ba co víc, protože je situace sféricky symetrická, můžeme si ji libovolně natočit, jak nám vyhovuje (obrázek 4.36 dole). Proto se v této kapitole budeme zabývat právě pouze rovníkovou (nebo také ekvatoriální) rovinou (v řeči kartézských soustav rovinou xy). Zjednodušíme si tím práci, protože místo čtyř prostoročasových souřadnic stačí zabývat se třemi, ale zároveň se nejedná o nefyzikální či výrazně limitující přístup.
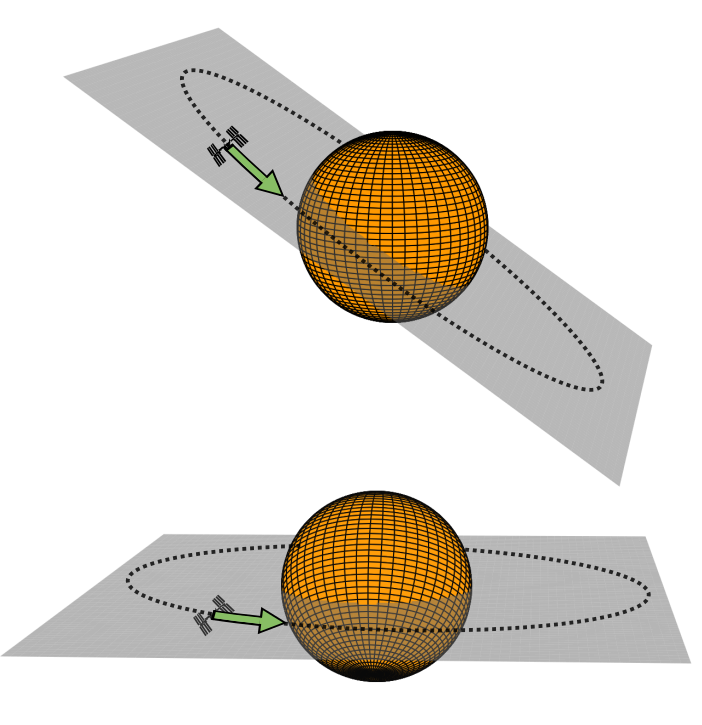
Obrázek 4.36 Nahoře: Těleso obíhající kolem sféricky symetrického tělesa obíhá v jedné rovině.
Dole: Situaci si můžeme vždy natočit tak, aby daná rovina byla v našem popisu horizontální (tzv. rovníková).
Připomeňme si, že metrika kartézské roviny \(xy\) je jednoduše \((\text{d}s)^2=(\text{d}x)^2+(\text{d}y)^2\) (rozdíly v souřadnici \(z\) jsou nulové). Pokud se na tuto rovinu budeme dívat jako na řez plochým prostoročasem (tedy zatím žádná gravitace), bude prostoročasová metrika této roviny \((\text{d}s)^2=-c^2(\text{d}t)^2+(\text{d}x)^2+(\text{d}y)^2\) (případně stačilo vzít jen vzorec (4.20) a omezit se na rovinu \(xy\)), kde souřadnice \((t,x,y)\) patří k nějaké námi zvolené inerciální vztažné soustavě. Pravoúhlé souřadnice nejsou v našem případě příliš praktické (hodně se budeme zabývat například vzdáleností od gravitujícího tělesa), takže si připomeňme polární souřadnice. Je to alternativní způsob popisu roviny, kdy místo kartézských souřadnic \((x,y)\) každému bodu přiřadíme jeho vzdálenost od počátku \(r\) (takové souřadnici se říká radiální) a úhel \(\varphi\), který svírá spojnice daného bodu a počátku s osou \(x\) (mrkněte znovu na obrázek 4.35). Prostoročasovou metriku roviny získáme také snadno. Protože u plochého prostoročasu nejsou časové a prostorové části metriky promíchány, stačí místo prostorové části metriky použít její verzi v polárních souřadnicích (4.17). Celkem tak pro rovinu v nezakřiveném případě dostáváme \begin{equation*}\tag{4.21}\label{4.21} (\text{d}s)^2=-c^2 (\text{d}t)^2+(\text{d}r)^2+r^2(\text{d}φ)^2. \end{equation*}
Podle Schwarzschildova řešení bude ale metrika prostoročasové roviny v okolí nerotujícího sféricky symetrického tělesa umístěného v počátku: \begin{equation*}\label{4.22}\tag{4.22} (\text{d}s)^2=-\left(1-\frac{2GM}{c^2r}\right)c^2(\text{d}t)^2+\frac{(\text{d}r)^2}{1-\frac{2GM}{c^2r}}+r^2(\text{d}\varphi)^2, \end{equation*} kde \(G\) je Newtonova gravitační konstanta, \(M\) je hmotnost tělesa a \(c\) je samozřejmě rychlost světla ve vakuu, takže metrika obsahuje dvě univerzální přírodní konstanty a parametr popisující situaci. Než se dostaneme k nějakým fyzikálním aplikacím, musíme prozkoumat několik důležitých vlastností této metriky včetně významu použitých souřadnic \((t,r,\varphi)\). Jelikož jsme si už rozmýšleli, že v přítomnosti gravitace se dějí zajímavé věci s délkami a časem, pravděpodobně vás nepřekvapí, že to s těmi souřadnicemi nebude tak jednoduché (i když bychom měli připomenout, že na konkrétních souřadnicích by žádná fyzikální situace neměla záviset, každou situaci můžeme stejně platně popsat nepřeberným množstvím souřadnic, jen některé volby budou vhodnější či názornější než jiné).
Začněme úhlovou souřadnicí \(\varphi\), protože to bude nejrychlejší. Porovnáme-li metriky \eqref{4.21} a \eqref{4.22}, vidíme, že v nich úhlová souřadnice vystupuje zcela stejně. I celý člen \(r^2(\text{d}\varphi)^2\) vypadá naprosto stejně (jak ale uvidíme, význam souřadnice \(r\) bude jiný). Prakticky to znamená, že v tečném směru (myšleno tečně k pomyslné kružnici \(r=konst\)) se neděje nic nového. To není tak udivující, když si uvědomíme, že celá situace je sféricky symetrická (v našem případě roviny spíše pouze kruhově symetrická). Tím pádem nemůže záležet na tom, na jaké úhlové souřadnici (tj. jakým směrem od zdroje) se nacházíme. Anebo jinak řečeno, protože sféricky symetrické těleso působí gravitačně pouze radiálně, projeví se očekávané zakřivení prostoru právě jen v závislosti metriky na radiální souřadnici.
O něco delší, ale stále celkem rychlý bude rozbor časové souřadnice \(t\), nazývané také souřadnicový čas. Již jsme se zmiňovali o tzv. gravitační dilataci času neboli skutečnosti, že v gravitačním poli plyne obecně čas v různých místech různě. Vidět je to přímo z metriky \eqref{4.22}. Pokud budeme stát na místě, tj. naše souřadnice \(r\) i \(\varphi\) budou konstantní, bude pro nás platit \(\text{d}r=\text{d}φ=0\) a metrika se zjednoduší na \begin{equation*}\label{4.23}\tag{4.23} (\text{d}s)^2=-\left(1-\frac{2GM}{c^2r}\right)c^2(\text{d}t)^2. \end{equation*}
Nyní je třeba si připomenout vlastní čas, který jsme si zatím jen zmínili ve třetí části. Tam jsme ukázali, že různým pozorovatelům může obecně různě plynout čas, a proto je třeba mezi nimi rozlišovat. Náš vlastní čas je ten, který nám pomyslně odtikává na hodinkách na ruce. Definičně je to čas v naší klidové soustavě. Označme si ho, jak je v relativitě zvykem \(\tau\) (tedy řeckým písmenem tau, které se ve fyzice používá skoro vždy, když už máme \(t\) zabrané). Pro vlastní čas z definice platí \((\text{d}s)^2=-c^2(\text{d}\tau)^2\) (což jsme ukázali v části o STR, pouze pro konečné rozdíly \(\Delta\) a ne nekonečně malé, které musíme používat v OTR, ale zde to platí stejně). Mínus v definici vlastního času je v pořádku, protože jak jsme se zmiňovali, kvadrát prostoročasového intervalu mezi dvěma událostmi, mezi kterými se pohybujeme podsvětelnou rychlostí (což my jako hmotná tělesa ani jinak nedokážeme), je v naší konvenci záporný. Definici vlastního času je dobré chápat tak, že pokud jsme přítomni dvěma událostem, dělí je z pohledu naší klidové soustavy pouze čas, nikoli prostor. Například vzpomeňte na relativistickou raketu z minulé části, která letěla mezi Zemí a Marsem. V soustavě rakety byla vzdálenost mezi odletem ze Země a příletem na Mars \(\Delta x^\prime\) nulová, protože raketa byla přítomna oběma událostem, takže se z jejího pohledu staly na stejném místě.
Pokud tedy dosadíme definici vlastního času do \eqref{4.23}, dostáváme \begin{equation*}\label{4.24}\tag{4.24} -c^2(\text{d}\tau)^2=-\left(1-\frac{2GM}{c^2r}\right)c^2(\text{d}t)^2\implies\text{d}\tau=\sqrt{1-\frac{2GM}{c^2r}}\text{d}t. \end{equation*} Tato vztah nám prakticky ukazuje souvislost mezi vlastním časem libovolného stojícího pozorovatele a plynutím časové souřadnice \(t\). Abychom ale konečně objasnili její význam, musíme si představit, že v rovnici \eqref{4.24} půjdeme se souřadnicí \(r\) velmi daleko. Ačkoli za chvilku uvidíme, že \(r\) nemá přímo význam radiální vzdálenosti od středu centrálního tělesa, i tak to znamená vzdalovat se směrem pryč. S narůstající vzdáleností je ve jmenovateli zlomku pod odmocninou čím dál tím větší číslo a zlomek je tím pádem čím dál tím menší. Pokud se pomyslně vzdálíme tak daleko, až bude zlomek prakticky nerozeznatelný od nuly (matematicky řečeno až se vzdálíme do nekonečna), bude pod odmocninou jednička. Jedná se prakticky o limitní proces, ale pokud jste na limity zatím nenarazili, přidržte se prostě té praktické představy být tak daleko, že už rozdíl zmíněné odmocniny a jedničky bude pod naši rozlišovací schopnost. Matematicky zapsáno \(\text{d}\tau\rightarrow\text{d}t\) pro \(r\rightarrow+\infty\) (což čteme „\(\text{d}\tau\) se blíží k \(\text{d}t\) pro \(r\) jdoucí do plus nekonečna“). To znamená, že \(t\) má význam vlastního času pozorovatele velmi vzdáleného od centrálního tělesa. Natolik vzdáleného, že prakticky necítí jeho gravitační účinky. Proč používáme právě tento čas jako souřadnici? Vzorec \eqref{4.24} naznačuje, že statickým pozorovatelům na různých radiálních souřadnicích plyne čas různě. To je právě efekt gravitační dilatace času. Nejste-li na stejném místě, bude vám a vaší kamarádce plynout čas jinak. Na čem se ale shodnete, je čas nekonečně vzdáleného pozorovatele \(t\), který si můžete z \eqref{4.24} oba dopočítat. Je to analogické tomu, když se na různých místech na Zemi používal čas Greenwichského poledníku pro synchronizaci hodin na celém světě (zde ale nejde samozřejmě o dilataci času, ale časová pásma). K problematice plynutí času se ještě detailněji vrátíme, nyní pojďme dokončit rozbor metriky prozkoumáním souřadnice \(r\).
Srovnáme-li opět metriky \eqref{4.21} a \eqref{4.22}, vidíme, že se jejich radiální členy, tj. ty s \((\text{d}r)^2\), znatelně liší. Nejen díky tomu už souřadnice \(r\) nemá přímo význam vzdálenosti od středu, jak jsme byli dosud zvyklí. Možná že máte z matematiky vycvičené oko a všimli jste si jmenovatele, ve kterém se odčítá a který obsahuje \(r\). To znamená, že je teoreticky možné, aby byl nulový, což je situace, která se nám v matematice samozřejmě vůbec nezamlouvá. Dělit nulou rozhodně nemůžeme. Kdy tento případ nastane? Jednoduchá podmínka nám říká, že tehdy, když bude \begin{equation*} 1-\frac{2GM}{c^2r}=0\iff 1=\frac{2GM}{c^2r}\iff r=\frac{2GM}{c^2}\equiv r_\text{S}. \end{equation*} Poslední výraz, který jsme si označili \(r_\text{S}\), se v OTR objevuje docela často a má také svůj název – Schwarzschildův poloměr. Jak ještě uvidíme, používá se zejména v souvislosti s černými dírami. Kromě univerzálních konstant závisí pouze na hmotnosti centrálního tělesa. Prozatím to pro nás bude jakási podivná hodnota, pro kterou metrika \eqref{4.22} přestává fungovat. Ve jmenovateli radiálního členu dělíme nulou a časový člen se vynuluje. To je první náznak toho, že se patrně nebude jednat o jednoduchou radiální vzdálenost, protože při jedné své konečné hodnotě nám z matematického hlediska přestanou vycházet smysluplné hodnoty. Je to trochu jakoby vám pásmový metr přestal fungovat, jakmile se dostanete třeba ke značce \(10\:\text{cm}\). V pozdější kapitole, která se dotýká problematiky černých děr, se na tuto oblast budeme muset lépe zaměřit. Zatím místo toho ale ukažme, že v běžných aplikacích si s touto podivnou hodnotou nemusíme lámat hlavu. Zkusme si pro názornost do Schwarzschildova poloměru dosadit pro dvě nám velmi známá vesmírná tělesa, Zemi a Slunce. V tabulce 4.4 vidíme porovnání hmotností těchto dvou těles, jejich výsledného Schwarzschildova poloměru a skutečného poloměru.
| Tabulka 4.4 Skutečný a Schwarzschildův poloměr pro Zemi a Slunce (zaokrouhlené na tři platné cifry) | |||
|---|---|---|---|
| hmotnost* | Schwarzsch. poloměr** | skutečný poloměr | |
| Země | \(5{,}97\cdot 10^{24}\:\text{kg}\) | \(8{,}87\:\text{mm} \) | \(6378\:\text{km}\) |
| Slunce | \(1{,}99\cdot 10^{30}\:\text{kg}\) | \(2950\:\text{m}\) | \(695700\:\text{km}\) |
| *Podle https://nssdc.gsfc.nasa.gov/planetary/factsheet/
**Zaokrouhleno na tři platné cifry. |
|||
Z tabulky vidíme, že jak Země, tak Slunce (a podobně to dopadne i pro jakýkoli reálný hmotný objekt s výjimkou černých děr) je mnohonásobně větší než jejich příslušný \(r_\text{S}\) (dokonce natolik, že můžeme pro toto srovnání ještě na chvilku ignorovat, že souřadnice \(r\) nemá přesně význam poloměru). Znamená to, že pro jakékoli běžné situace, ať už jste na povrchu planety, obíháte ji anebo třeba nějakou hvězdu, nikdy se nemůžete dostat na úroveň Schwarzschildova poloměru, takže nás podivné chování metriky pro tuto hodnotu souřadnice nemusí nutně trápit. Je třeba se jím zabývat až v situaci, kdy je rozměr tělesa srovnatelný s jeho hodnotou \(r_\text{S}\) či (alespoň teoreticky) menší. Proto se také odteď dohodněme, že nebude-li řečeno jinak, budeme vždy uvažovat hodnoty \(r>r_\text{S}\). Tím se zároveň vyhneme i druhé problematické hodnotě souřadnice \(r\). Další hodnota, která nám matematicky podle (4.22) vadí je \(r=0\), protože pak máme nulu ve jmenovateli zlomku. Narazili jsme tak na první náznaky podivného chování Schwarzschildova řešení, které před více jak sto lety vyústilo v předpověď černých děr – objektů, které nepřestávají lidstvo fascinovat a teprve v poslední době je začínáme pomalu ale jistě zkoumat nejen čistě teoreticky. I o nich si něco povíme, ale necháme si to až do samostatné podkapitoly.
Poznámka 4.9
Poznamenejme, že se do problematické situace nemůžeme dostat, ani kdybychom se hypoteticky prokopali skrz těleso až na úroveň Schwarzschildova poloměru či nulové souřadnice \(r\). Metrika \eqref{4.22} je platná totiž pouze buď vně nerotujícího sféricky symetrického tělesa (což je situace, které se budeme hlavně věnovat), nebo v případě stejně tak nerotující a nenabité černé díry (o čemž se zmíníme později). Pro prostoročas uvnitř kulového tělesa s konstantní hustotou (jedná se tedy o zjednodušený model) existuje jiné, tzv. vnitřní Schwarzschildovo řešení, které podobný problém s radiální souřadnicí nemá, ale nebudeme se jím zde detailněji zabývat, protože ho ve fyzikálních aplikacích nebudeme potřebovat. Chceme-li se například bavit o planetách obíhajících hvězdu, nemá smysl řešit, jak vypadá prostoročas uvnitř hvězdy, protože pokud by se planeta dostala až k hvězdnému povrchu, bude s největší pravděpodobností zničena. Otázka struktury prostoročasu uvnitř hvězd je například důležitá pro astrofyziky, kteří zkoumají zákonitosti fungování hvězd samotných, nicméně tomuto tématu se zde věnovat nebudeme. Náš přístup bude tedy velmi pragmatický. Dokud se nezabýváme černými dírami, souřadnicový problém ve Schwarzschildově metrice nemusíme řešit.
Co je to tedy zač ta souřadnice \(r\)? Nejlépe si to ukážeme na výpočtu obvodu kružnice kolem centrálního tělesa. Jinými slovy, budeme se držet na konstantním \(r\), takže v metrice \eqref{4.22} bude tentokrát \(\text{d}r=0\), a protože vzdálenost měříme v nějakém konkrétním čase (v řeči relativity určujeme vzdálenost jako prostoročasový interval mezi dvěma událostmi současnými z hlediska souřadnicového času \(t\)), bude i \(\text{d}t=0\). Pro malý kousek obvodu \(o\) tedy dostáváme \begin{equation*} (\text{d}o)^2=r^2(\text{d}\varphi)^2\implies\text{d}o=r\,\text{d}\varphi. \end{equation*} Získat celý obvod pak znamená “posčítat” tyto malé kousky přes celý rozsah úhlové souřadnice \(\varphi\), tj. od \(0\) do \(2\pi\). Tento výpočet bude ve skutečnosti velmi lehký, protože jak postupně jdeme po kružnici, souřadnice \(r\) zůstává konstantní, takže se dá před integraci vytknout a my sčítáme opravdu jen malé kousky úhlu \(\text{d}\varphi\), čímž dostaneme plný úhel \(2\pi\). Podrobně rozepsán vypadá výpočet takto \begin{equation*} o=\int_{\text{kružnice}}\text{d}o=\int_0^{2\pi}r\,\text{d}\varphi=r∫_0^{2\pi}\text{d}\varphi=r\,2\pi=2\pi r. \end{equation*} Vyšel nám notoricky známý vztah pro obvod kružnice v eukleidovské geometrii, který můžeme zároveň chápat jako definici souřadnice \(r\). Význam souřadnice \(r\) (můžeme ji nazvat obvodovým poloměrem) je tedy dán obvodem pomyslné kružnice, na které se nacházíme, vyděleným \(2\pi\). Mimochodem, pokud bychom pracovali s celým prostorem a ne jen s rovinou, stejně tak by nám vyšlo, že povrch pomyslné sféry, na níž se v danou chvíli nacházíme, je \(4\pi r^2\).
Co se týče tečného směru, chová se souřadnice \(r\) celkem „klasicky“. To zajímavé ale nastane, pokud se pokusíme vyjádřit pomocí \(r\) skutečnou radiální vzdálenost. Dejme tomu, že máme značky na pevně zvolených hodnotách \(r_1\) a \(r_2\) o stejné úhlové souřadnici (tj. na stejné radiále \(\varphi=konst\)), přičemž předpokládejme čistě pro pořádek, že \(r_2>r_1\), a zároveň připomeňme, že se pohybujeme zatím vždy v oblasti, kde platí \(r>r_\text{S}\). Chtěli bychom změřit reálnou vzdálenost mezi značkami, označme si ji třeba \(Δl\). Je to vlastně stejná úloha, jako když jsme na sféře chtěli změřit vzdálenost mezi dvěma body, které se lišily třeba jen zeměpisnou šířkou.
Odpověď nám dá přesně naše metrika, která se pro tuto situaci opět výrazně zjednoduší, protože oba body mají stejnou úhlovou souřadnici, takže \(\text{d}\varphi=0\), a protože opět měříme čistě vzdálenost, bude i \(\text{d}t=0\). Jelikož je \(\text{d}t\) nula, představuje zbylá část metriky právě malý přírůstek hledané prostorové vzdálenosti. Označme si ji proto \(\text{d}l\): \begin{equation*}\tag{4.25}\label{4.25} (\text{d}s)_{prostor}^2\equiv(\text{d}l)^2=\frac{(\text{d}r)^2}{1-\frac{r_\text{S}}{r}}\iff \text{d}l=\frac{\text{d}r}{\sqrt{1-\frac{r_\text{S}}{r}}}. \end{equation*} Pro pochopení tohoto vztahu je dobré si připomenout význam metrických koeficientů z kapitoly 4.2. Malá změna souřadnice o \(dr\) způsobí malé posunutí v radiální vzdálenosti \(\text{d}l\), přičemž podle \eqref{4.25} není jedno, kde se nacházíme – vztah závisí na hodnotě souřadnice \(r\). Protože platí \(r>r_\text{S}\), je výraz ve jmenovateli vždy menší než jedna a skutečné posunutí je tím pádem větší než \(\text{d}r\). Abychom určili hledanou vzdálenost mezi \(r_1\) a \(r_2\), budeme muset vztah \eqref{4.25} integrovat. Výsledek můžeme opět najít pomocí stránky Wolfram Alpha. Nejedná se o zrovna jednoduchý vztah, nicméně uveďme si ho aspoň pro představu. Skutečná vzdálenost mezi body o souřadnici \(r_1\) a \(r_2\) vychází jako \begin{equation*}\label{4.26}\tag{4.26} \Delta l = r_2\sqrt{1-\frac{r_\text{S}}{r_2}}+\frac{1}{2}r_\text{S}\ln{\left(\frac{1+\sqrt{1-\frac{r_\text{S}}{r_2}}}{1-\sqrt{1-\frac{r_\text{S}}{r_2}}}\right)}-r_1\sqrt{1-\frac{r_\text{S}}{r_1}}-\frac{1}{2}r_\text{S}\ln{\left(\frac{1+\sqrt{1-\frac{r_\text{S}}{r_1}}}{1-\sqrt{1-\frac{r_\text{S}}{r_1}}}\right)}. \end{equation*}
Nemusíte se děsit. Přímo počítat s tímto výrazem nebudeme. Jde nám spíš o to ukázat, že daný vztah existuje. Hlavně nám ale ukazuje, že souřadnice \(r\) opravdu nemá význam radiální vzdálenosti. Kdyby měla, vyšlo by nám jednoduše \(\Delta l\) rovno \(r_2-r_1\). Než abychom vztah \eqref{4.26} nějak komplikovaně zkoumali, pojďme do něj zkusit dosadit. Všimněme si, že kromě volby \(r_1\) a \(r_2\) závisí výsledek také na \(r_\text{S}\), tedy potažmo na hmotnosti centrálního gravitujícího tělesa. Abychom ale nemuseli situaci zkoumat pro mnoho různých nastavení hmotnosti, použijeme malého matematického triku, kdy budeme souřadnice \(r\) vyjadřovat jako násobky Schwarzschildova poloměru, např. \(r_1=10r_\text{S}\) apod. Nejen že se nám \(r_\text{S}\) pak zkrátí v odmocninách, ale výsledná vzdálenost \(\Delta l\) také vyjde jako násobek \(r_\text{S}\). Náš popis tak bude nezávislý na tom, v okolí jakého centrálního tělesa se zrovna nacházíme. Zkusme porovnat předpověď \eqref{4.26} s rozdílem radiálních souřadnic \(\Delta r=r_2-r_1\), což je tedy hodnota, kterou bychom očekávali, pokud by v gravitačním poli platila eukleidovská geometrie. Jediná mírná komplikace je, že výsledek závisí na volbě obou souřadnic, to znamená nejenom na jejich rozdílu, ale také kde naše měření začíná. Rozdělíme si proto srovnání na dvě situace. V tabulce 4.5 budeme nejprve udržovat konstantní rozestup souřadnic například \(\Delta r=3r_\text{S}\) a budeme měnit počáteční souřadnici \(r_1\) v násobcích \(r_\text{S}\) (v prvním řádku tabulky je tedy \(r_1=2r_\text{S}\) a \(r_2=5r_\text{S}\)). V pravém sloupci je spočítána relativní chyba, které bychom se dopustili, kdybychom zakřivení prostoru neuvažovali a předpokládali platnost hodnoty \(\Delta r\). Podobně tomu bude i v tabulce 4.6, kde budeme naopak držet konstantní počáteční souřadnici například \(r_1=2r_\text{S}\) a měnit \(r_2\), a tím i \(\Delta r\). Poznamenejme ještě, že reálně se dostat na tak malé násobky \(r_\text{S}\) by bylo možné jen u extrémně kompaktních objektů, jako jsou černé díry nebo velmi hmotné neutronové hvězdy. Tuto diskuzi si ale necháme na později.
| Tabulka 4.5 Porovnání rozdílu radiálních souřadnic a příslušné skutečné radiální vzdálenosti pro \(\Delta r=3r_\text{S}\) |
||
|---|---|---|
| \(r_1/r_\text{S}\) | \(\Delta l/r_\text{S}\) | err / % |
| \(2\) | \(3{,}620184281\) | \(17{,}1\) |
| \(10\) | \(3{,}140527940\) | \(4{,}5\) |
| \(50\) | \(3{,}029565977\) | \(1{,}0\) |
| \(100\) | \(3{,}014889529\) | \(0{,}5\) |
| \(200\) | \(3{,}007472131\) | \(0{,}2\) |
| \(500\) | \(3{,}002995516\) | \(0{,}1\) |
| \(1000\) | \(3{,}001498877\) | \(0{,}05\) |
| Tabulka 4.6 Porovnání rozdílu radiálních souřadnic a příslušné skutečné radiální vzdálenosti pro \(r_1=2r_\text{S}\) |
||
|---|---|---|
| \(\Delta r/r_\text{S}\) | \(\Delta l/r_\text{S}\) | err / % |
| \(1\) | \(1{,}300118428\) | \(23{,}1\) |
| \(10\) | \(11{,}10762238\) | \(10{,}5\) |
| \(50\) | \(51{,}86591191\) | \(3{,}6\) |
| \(100\) | \(102{,}2063549\) | \(2{,}2\) |
| \(200\) | \(202{,}5498336\) | \(1{,}3\) |
| \(500\) | \(503{,}0061125\) | \(0{,}6\) |
| \(1000\) | \(1003{,}352062\) | \(0{,}3\) |
Z první tabulky vyplývá, že zakřivení je tím silnější, čím jsme blíže, což nás jistě nepřekvapuje. Dalo se očekávat, že blíže centrálnímu tělesu, tj. v silnějším gravitačním poli, budou účinky na geometrii prostoru silnější a se zvětšující se vzdáleností se prostorové zakřivení stává méně výrazné, až někde dostatečně daleko bude prakticky neměřitelné. To samozřejmě platí pro všechny gravitační efekty, se vzdáleností od centrálního tělesa slábnou. Je to vlastně přímo vidět z metriky \eqref{4.22}, která pro \(r\) jdoucí do nekonečna přechází v plochou metriku \eqref{4.21}, protože zlomek \(2GM/c^2r\) jde k nule. Podobně ve druhé tabulce vidíme, že čím dál je koncová souřadnice, tím je také náš výsledek méně ovlivněn zakřivením, ale relativní odchylka neklesá tak rychle jako v prvním případě. To je dáno tím, že v našem výpočtu držíme \(r_1=2r_\text{S}\), takže blízká oblast největšího zakřivení je zahrnuta v každém z intervalů, ale pro delší vzdálenosti již tvoří menší část celku.
Je třeba upozornit, že zde nijak nepracujeme s reálným rozměrem gravitujícího tělesa. Stále platí, že má-li metrika \eqref{4.22} fungovat, musíme být mimo centrální těleso (ono taky ptát se, jak se budeme pohybovat či jak dopadnou naše měření uvnitř hvězdy či planety pro nás nemá moc význam). Zabýváme-li se tak např. radiální souřadnici \(r=2r_\text{S}\), automaticky zde předpokládáme, že daný objekt má bezpečně menší rozměry. Znamená to tedy, že pokud bychom chtěli naměřit silné zakřivení prostoru, museli bychom se dostat blízko velmi hmotných a zároveň kompaktních objektů. Například jak už víme, Schwarzschildův poloměr Slunce jsou necelé \(3\:\text{km}\), zatímco skutečný poloměr Slunce je zhruba \(696340\:\text{km}\), což odpovídá více jak \(232000\)krát násobku \(r_\text{S}\). I na povrchu Slunce je tak gravitační zakřivení prostoru miniaturní a rozdíl mezi radiální souřadnicí a reálnou vzdáleností zanedbatelný. Na povrchu Země jsme téměř \(709\) milionkrát dále než je Schwarzschildův poloměr Země, což také vysvětluje, proč nám eukleidovská geometrie tak dobře funguje. Je to podobné jako když jsme si ve speciální relativitě vysvětlovali, že dilataci času a kontrakci délek na Zemi běžně nepozorujeme, protože se nepohybujeme dostatečně rychle vůči rychlosti světla anebo neumíme měřit dostatečně přesně (většinou obojí). S gravitací je to podobné. Gravitační zakřivení prostoru máme šanci naměřit jen u velmi hmotných a zároveň kompaktních astronomických těles, jako jsou například neutronové hvězdy. Kupříkladu objekt s označením PSR J0740+6620, patřící mezi nejhmotnější známé neutronové hvězdy, je přibližně dvakrát hmotnější než Slunce, ale jeho poloměr je odhadován na \(13\:\text{km}\). Tj. něco málo více než dvojnásobek jeho \(r_\text{S}\). Ne nadarmo bývají neutronové hvězdy nazývány relativistické laboratoře, protože jsou ideálními objekty na proměřování a ověřování předpovědí obecné relativity. V tomto ohledu se o nich také ještě zmíníme.
Diagram vnoření
Strávili jsme již docela dost času nad významem použitých souřadnic ve Schwarzschildově metrice, zejména nad vztahem mezi souřadnicí \(r\) a radiální vzdáleností, který nám naznačoval něco o zakřivení prostoru v gravitačním poli. Ukažme si ještě praktický způsob, jak toto zakřivení zviditelnit a tím pádem lépe pochopit. Diagramy vnoření (ang. embedding diagrams) jsou nástroj, jak vizualizovat neeukleidovskou geometrii nějaké zkoumané situace jejím vnořením do eukleidovského prostoru. Jedná se tedy o obecnou techniku používanou nejenom v OTR, ale my se budeme zabývat jen jedním jejím konkrétním příkladem. U obrázku 4.21 jsme si zkoušeli jednoduchou aktivitu, kdy jsme demonstrovali účinky neeukleidovské geometrie v rovině na přímočarou trajektorii tělesa. Abychom zakřivení dosáhli, museli jsme rovinu „vytáhnout“ do třetího rozměru, který ale sloužil čistě k vizualizaci a neměl fyzikální význam (tj. pohyb byl stále dvourozměrný). My nyní uděláme něco podobného. Vnoříme ekvatoriální rovinu Schwarzschildova prostoročasu do eukleidovského prostoru. Zjednodušeně to znamená, že naši rovinu ztotožníme s kartézskou rovinou \(xy\) a zdeformujeme ve třetím rozměru \(z\) tak, aby výsledná plocha měla stejnou prostorovou křivost jako ekvatoriální rovina popsaná metrikou \eqref{4.22} (ilustraci vidíme na obrázku 4.37). Zakřivené plochy v prostoru je totiž něco, co dokážeme dobře chápat a hlavně vizualizovat. Prakticky tedy potřebujeme najít předpis, který každému bodu v rovině \(xy\) přiřadí tu správnou výšku \(z\). Vlastně je naše situace ještě o něco jednodušší, protože víme, že Schwarzschildovo řešení je sféricky symetrické, v našem případě zkoumání roviny tedy vlastně rotačně symetrické. Stejnou vlastnost tedy musí mít i hledaná plocha. Stačí nám tedy najít výškový profil plochy v závislosti na vzdálenosti od středu \(z(r)\), a graf této funkce pak zrotovat dokola kolem osy \(z\). K výpočtu této funkce jsou zapotřebí derivace a integrály, takže ho zde nebudeme provádět, ale zájemci si ho mohou rozbalit níže.
Naším cílem je najít tvar plochy tak, aby její křivost odpovídala prostorové křivosti ekvatoriální roviny Schwarzschildova prostoročasu. Protože nám jde pouze o prostorovou geometrii (celá prostoročasová se velmi těžko nějak vizualizuje), nejprve si přepíšeme metriku \eqref{4.22} pro nějaký konkrétní čas \(t=konst\): \begin{equation*} (\text{d}s)^2=\frac{(\text{d}r)^2}{1-\frac{r_\text{S}}{r}}+r^2(\text{d}\varphi)^2. \end{equation*} Dále potřebujeme metriku eukleidovského prostoru, ve kterém budeme zakřivenou plochu zobrazovat. Tu už dobře známe jako \((\text{d}s)^2=(\text{d}x)^2+(\text{d}y)^2+(\text{d}z)^2\). Díky rotační symetrii (a hlavně podobnosti se Schwarzschildovskými souřadnicemi) bude výhodné zde použít polární souřadnice pro rovinu \(xy\). Tím se nám změní členy s přírůstky souřadnic \(x\) a \(y\), ale \(z\) zůstane beze změny. Vzpomeneme-li na (4.17), bude mít metrika prostoru tvar \begin{equation*} (\text{d}s)^2=(\text{d}r)^2+r^2(\text{d}\varphi)^2+(\text{d}z)^2. \end{equation*} Vlastně zde eukleidovský prostor popisujeme v tzv. válcových souřadnicích, což je prakticky kombinace roviny v polárních souřadnicích s přidanou výškou (konvenčně souřadnice \(z\)). Vnoření se provede formálně tak, že tyto dvě metriky dáme do rovnosti. Na první pohled nám může připadat zvláštní dávat rovnost mezi metriku plochy a prostoru, tj. různě rozměrných objektů. My ale ve skutečnosti hledáme pouze jednu konkrétní zakřivenou plochu, respektive její profil jako funkci \(z(r)\). Přírůstky \(\text{d}z\) a \(\text{d}r\) tedy podle našeho předpokladu nejsou nezávislé a proto se nejedná ve skutečnosti o celý prostor, ale jen jeho dvourozměrný řez. Vidíme, že úhlové členy \(r^2(\text{d}\varphi)^2\) jsou v obou metrikách stejné. Zbyde nám \begin{equation*} (\text{d}r)^2+(\text{d}z)^2=\frac{(\text{d}r)^2}{1-\frac{r_\text{S}}{r}}. \end{equation*} Tuto rovnici dále upravíme tak, abychom dostali výraz pro \(\text{d}z/\text{d}r\): \begin{align*} (\text{d}z)^2&=\frac{(\text{d}r)^2}{1-\frac{r_\text{S}}{r}}-(\text{d}r)^2=(\text{d}r)^2 \left[\frac{1}{1-\frac{r_\text{S}}{r}}-1\right]=(\text{d}r)^2\left[\frac{\frac{r_\text{S}}{r}}{1-\frac{r_\text{S}}{r}}\right]=(\text{d}r)^2\left[\frac{r_\text{S}}{r-r_\text{S}}\right] \\ \frac{(\text{d}z)^2}{(\text{d}r)^2}&=\frac{r_\text{S}}{r-r_\text{S}}\implies\frac{\text{d}z}{\text{d}r}=±\sqrt{\frac{r_\text{S}}{r-r_\text{S}}} \end{align*} Poslední výraz je prakticky vzato derivace funkce \(z\) podle \(r\), jinými slovy předpis pro tečnu grafu hledané funkce \(z(r)\) pro danou hodnotu \(r\). Samotnou \(z(r)\) pak najdeme integrací tohoto vztahu: \begin{align*} z(r)&=\int \text{d}z=\int\frac{\text{d}z}{\text{d}r}\text{d}r=\int±\sqrt{\frac{r_\text{S}}{r-r_\text{S}}}dr=±\sqrt{r_\text{S}} \int\frac{dr}{\sqrt{r-r_\text{S}}} \\ &=±2\sqrt{r_\text{S}}\sqrt{r-r_\text{S}}+konst=±2\sqrt{r_\text{S}r-r_\text{S}^2}+konst. \end{align*} Před samotnou integrací jsme vytknuli konstantu \(\sqrt{r_\text{S}}\) před integrál. Protože integrace je prakticky vzato výpočet opačný k derivaci a integrovaná funkce je poměrně jednoduchá, dá se výsledek v podstatě uhádnout díky znalostem pravidel o derivování. Můžete si ho zkusit ověřit tím, že výsledek zderivujete podle \(r\), a uvidíte, že dostanete výchozí výraz. Aditivní konstanta přičtená k výsledku nám vychází vždy, když počítáme neurčitý integrál, tedy hledáme čistě předpis funkce ze známé derivace bez dosazování nějakých konkrétních integračních mezí. Prakticky to znamená, že hledaná funkce může být posouvána libovolně „nahoru či dolů“ a stále bude mít stejnou derivaci. Z fyzikálního hlediska to znamená, že je jedno, jak moc nad či pod ekvatoriální rovinou hledanou plochu vykreslíme, její křivost bude stále stejná a nic důležitého se pro nás nezmění. Můžeme tedy klidně danou konstantu položit rovnou nule, abychom se jí nemuseli zabývat.
Z metriky \eqref{4.22} vychází, že aby měla hledaná plocha stejnou křivost jako ekvatoriální rovina Schwarzschildova prostoročasu, musí její výškový profil splňovat \begin{equation*}\tag{4.27}\label{4.27} z(r)=±2\sqrt{r_\text{S}r-r_\text{S}^2}. \end{equation*} Znaménko \(±\) před funkcí prakticky znamená, že danou plochu můžeme vytáhnout „nad i pod“ ekvatoriální rovinu, v obou případech bude mít stejnou křivost. Prozatím si tedy pro jednoduchost vyberme výsledek se znaménkem plus a později tuto volbu ještě okomentujeme. Kladnou volbu funkce vidíme vykreslenou na obrázku (4.37) vlevo (záporná by byla vykreslena zrcadlově pod osou \(x\)). Nejedná se o nijak komplikovanou funkci, vzhledem k tomu, že \(r_\text{S}\) je pro daný centrální objekt konstanta, tak má funkce tvar \(\sqrt{ax-b}\), kde \(a\) a \(b\) jsou konstanty. Jedná se tedy o posunutou odmocninovou funkci (což je prakticky vzato polovina paraboly překlopená kolem osy prvního a třetího kvadrantu, protože odmocninová funkce je inverzní, tj. opačná, ke kvadratické funkci, jejímž grafem je parabola). Snadno také z předpisu \eqref{4.27} vidíme, že výraz je definovaný jen pro \(r≥r_\text{S}\), což je v souladu s tím, že, jak jsme viděli, pro tuto hodnotu radiální souřadnice Schwarzschildova metrika matematicky selhává. Hledaná plocha nazývaná Flammův paraboloid pak vznikne rotací grafu funkce kolem osy \(z\) (obrázek 4.37 vpravo). Díra uprostřed odpovídá podmínce platnosti odmocninové funkce. Opět připomeňme, že v reálných aplikacích nám to nevadí, protože běžná tělesa jsou rozlehlejší než jejich odpovídající Schwarzschildův poloměr, takže se na \(r=r_\text{S}\) není možné dostat, aniž bychom nenarazili do povrchu planety či nebyli pohlceni hvězdou.
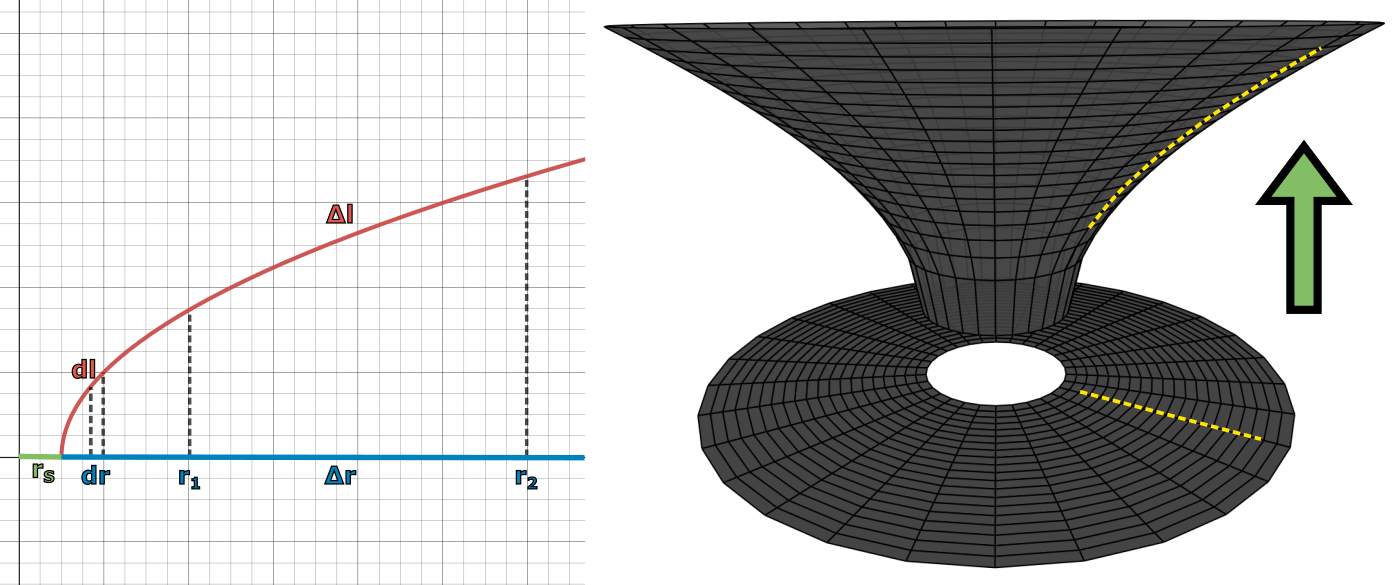
Obrázek 4.37 Vlevo: Graf funkce \eqref{4.27} je výškovým profilem hledané plochy, jejíž křivost odpovídá prostorové křivosti ekvatoriální roviny Schwarzschildova prostoročasu. Je naznačen vztah mezi malým přírůstky radiální souřadnice \(\text{d}r\) a skutečné vzdálenosti \(\text{d}l\) (vztah \eqref{4.25}), stejně tak pro konečné změny \(\Delta r\) a \(\Delta l\) (vztah \eqref{4.26}). Vidíme, že vztah nefunguje pro hodnoty \(r\lt r_\text{S}\).
Vpravo: Flammův paraboloid získáme rotací grafu funkce \eqref{4.27} kolem osy \(z\), protože víme, že zkoumaná situace je rotačně symetrická. Prakticky si můžeme představovat, že ekvatoriální rovinu zdeformujeme tak, abychom viděli zakřivení, které zde předpovídá obecná relativita.
Flammův paraboloid je z matematického hlediska relativně jednoduchá plocha, takže ji můžeme také vytisknout na 3D tiskárně, abychom s ní mohli pracovat podobně jako u zakřivených ploch dříve. Příklad vidíte na obrázku 4.38 vlevo. Úzký pruh papíru představuje geodetiku na ploše, tedy trajektorii volné částice. Její dráha je zakřivena čistě díky nenulové křivosti plochy. Všimněte si také, že na obrázku je paraboloid otočen otvorem vzhůru. To souvisí právě se znaménky \(±\) v rovnici \eqref{4.27}. Plochu můžeme používat obrácenou otvorem nahoru i dolů, ale vždy je třeba si daný pohyb představovat přímo v ploše, nikoli na ní – třebaže tvar paraboloidu svádí k použití jako trychtýř, do které bychom mohli hodit kuličku a nechat ji obíhat (o této aktivitě se ještě zmíníme). Na obrázku je celá situace zabrána kolmo, což je velmi důležité, protože připomeňme, že celou dobu zkoumáme pohyb v rovině, tedy dvourozměrnou situaci (třírozměrnou, pokud započítáme i čas). Vydutí roviny do třetího prostorového rozměru slouží pouze k vizualizaci jinak neviditelné geometrie ekvatoriální roviny. Názorněji to vidíme na obrázku 4.38 vpravo, kde je záběr z appletu, který si můžete sami vyzkoušet.
 |
Obrázek 4.38 Vlevo: Model geodetiky na Flammově paraboloidu. Pohled shora připomíná, že na situace je třeba se dívat jako na dvourozměrnou, zakřivení plochy do třetího rozměru slouží pouze ke zviditelnění neeukleidovské geometrie ekvatoriální roviny. Připomeňme, že pro skutečný popis gravitace potřebujeme zakřivení prostoročasu, ale Flammův paraboloid zobrazuje pouze prostorové zakřivení (omezené na jednu rovinu). Je to tedy jen jednoduchý model, který má demonstrovat obecnější princip. Například na něm geodetiky nemohou vytvořit uzavřenou orbitu, jako to vidíme u planet.
Vpravo: Záběr z appletu demonstrujícího stejný princip.
Poznámka 4.10
V předchozí poznámce jsme se zmínili o vnitřím Schwazschildově řešení, které popisuje prostoročas uvnitř sféricky symetrického tělesa o konstantní hustotě. I pro něj je možné vytvořit diagram vnoření a sloučit ho s Flammovým paraboloidem. To je možné díky tomu, že obě řešení na sebe přesně navazují na povrchu tělesa. Doplněný diagram vidíme na obrázku.
 |
Obrázek 4.39 Spojení diagramů vnoření pro vnější a vnitřní Schwarzschildovo řešení Einsteinových rovnic. Pro lepší představu je zobrazeno i centrální těleso (například hvězda). Vidíme, že diagramy na sebe navazují na povrchu tělesa a žádný problém se souřadnicemi nenastává. Stále má ale význam uvažovat jen obíhání těles ve vnější části, protože dopadem na povrch tělesa by pravděpodobně došlo k jejich zničení.
Podobné obrázky jsou čtenáři jistě povědomé. Jedná se o nejčastější ilustraci spojovanou s obecnou teorií relativity či zakřivením prostoročasu. Stačí některé z podobných hesel zadat do vyhledavače obrázků a hned na nás vyskočí doslova stovky podobných vyobrazení. Podobně jako je třeba rovnice \(E=mc^2\) nejslavnějším reprezentantem speciální teorie relativity pro širokou veřejnost, jsou tyto diagramy ikonami obecné relativity (my jsme ho už také potkali na obrázku 4.22). Vedly také k často zmiňované analogii, že „prostoročas kolem hmotných těles je jako pružná látka, na kterou jsme položili těžké těleso, a látka se tím zdeformovala“. Tuto analogii může často vidět i jako praktickou demonstraci. Samozřejmě se jedná jen o model, který je sice velmi názorný a hravý, ale má celou řadu praktických nedostatků. Za prvé tvar prohnutí látky samozřejmě nemusí a pravděpodobně nikdy přesně neodpovídá rovnici \eqref{4.27}. Ale i kdyby se nám to podařilo, kuličky se nebudou pohybovat po geodetikách, protože na ně působí skutečná gravitace, kterou se ale v této demonstraci snažíme modelovat právě zakřivením plochy. A jsou tu i další důvody. Působí na ně tření a odpor vzduchu, nepohybují uvnitř plochy, ale na ní, a zároveň se kuličky po ploše valí, takže do hry vstupuje i jejich moment setrvačnosti – obecně se nechovají zcela jako hmotné body.
Na druhou stranu se této demonstraci nedá upřít její význam, protože se na ní dá mnoho jevů přibližně ukázat (jak je vidět například v odkazovaném videu) a zejména pro mladší studenty je celkem zajímavá (i když osobní zkušenost ukazuje, že pouštět kuličky do gravitační studny je zábava v každém věku). Zároveň se taková prohnutá plocha dá použít i jako demonstrace klasické gravitace. Dá se totiž ukázat (vizte odvození níže), že pokud bude mít plocha hyperbolický profil, tj. bude prohnutá jako funkce \(-k/r\), kde \(k\) je nějaká vhodně zvolená konstanta, bude na kuličky působit dostředivá síla úměrná \(1/r^2\), jako v klasické gravitaci. Vytvořit přesně hyperbolické zahnutí plochy pomocí pružné látky je samozřejmě také velmi obtížné až nereálné, takže skutečná deformace látky bude hyperbole pravděpodobně stejně vzdálená jako parabole. Proto se také prakticky stejná aktivita používá jak pro demonstraci gravitace v klasickém slova smyslu, tak relativistickém.
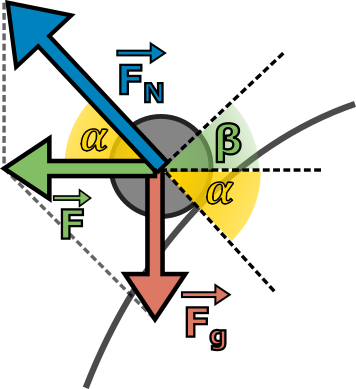
Kulička na ploše včetně působících sil \(\vec{F_\text{G}}\) a \(\vec{F_N}\) a jejich výslednice \(\vec{F}\). Tangens úhlu \(\beta\) je směrnice tečny k ploše, takže přímo derivace hledané funkce popisující tvar plochy.
Na obrázku vpravo máme nákres zobrazující kuličku na ploše včetně sil, které na ni působí. Jsou to tíhová síla \(\vec{F_\text{G}}\) svisle dolů, jejíž velikost standardně spočítáme jako \(F_\text{G}=mg\), kde \(m\) je hmotnost kuličky a \(g\) tíhové zrychlení. Na kuličku dále působí reakční síla plochy, označili jsme ji \(\vec{F_N}\) jako normálovou sílu (je totiž vždy kolmá na daný povrch, neboli má směr normály k povrchu). Požadujeme, aby jejich složením vznikla výsledná síla \(\vec{F}\), která bude mít dostředivý směr a její velikost bude ubývat se čtvercem vzdálenosti od středu, jako tomu je u gravitační síly v centrálním poli. Síly tvoří pravoúhlý trojúhelník, ve kterém platí \begin{equation*} \tan{\alpha}=\frac{F_\text{G}}{F}\implies F=\frac{F_\text{G}}{\tan{\alpha}}=\frac{mg}{\tan{α}}. \end{equation*} Abychom určili profil plochy jako průběh funkce \(z(r)\) (jejíž význam je podobný jako u diagramu vnoření), využijeme úhel \(\beta\), který svírá tečna k ploše v daném místě s vodorovným směrem. Tangens tohoto úhlu je tedy směrnicí tečny, a tím pádem derivací \(z^\prime(r)\) příslušné funkce v daném bodě. Z obrázku je vidět, že platí \(\alpha+\beta=90°\), takže \(\alpha=90°-\beta\). Dosadíme tedy za \(\alpha\), a s využitím vlastností goniometrických funkcí můžeme ukázat, že \begin{equation*} \tan{\alpha}=\tan{(90°-\beta)}=\frac{\sin{(90°-\beta)}}{\cos{(90°-\beta)}}= \frac{\cos{\beta}}{\sin{\beta}}=\frac{1}{\tan{\beta}}=\frac{1}{z^\prime(r)}. \end{equation*} Dohromady dostáváme \(F=mgz^\prime(r)\). Dle našeho požadavku má být \(F\sim r^{-2}\), položme tedy \(z^\prime(r)=k/r^2\), kde \(k\) je nějaká konstanta. Ze znalosti pravidel derivace můžeme rovnou uhodnout, že řešením je hledaná funkce \(z(r)=-k/r.\)
Náš výsledek vám je možná povědomý, má totiž podobný tvar jako newtonovský gravitační potenciál \(-GM/r\), jemuž odpovídá gravitační potenciální energie v centrálním poli \(E_P=-mGM/r\). Pozor, jedná se o jinou situaci, než je notoricky známá potenciální energie v homogenním gravitačním poli \(E_P=mgh\), protože tento vzorec platí jen v případě, kdy gravitační zrychlení můžeme pokládat za konstantní. I pro klasický popis gravitace je ale pohyb kuliček po zakřivené ploše pouze kvalitativní model, který obecně přesně neodpovídá reálnému pohybu hmotných bodů v gravitačním poli.
Hlavním problémem diagramu vnoření a z něj vycházejících demonstrací je, že zobrazuje pouze prostorovou křivost, z podstaty věci neobsahuje žádnou informaci o čase. A jak už jsme viděli, k plnému popsání gravitace je zapotřebí zakřivení prostoročasu. Na Flammově paraboloidu například nenajdeme geodetiky reprezentující stabilní orbitu, což například u planet obíhajících Slunce jednoznačně pozorujeme. Podobně jako zeměpisné rovnoběžky nejsou geodetiky na sféře, křivky pro konstantní radiální souřadnici (tj. kružnice vzniklé kolmým řezem na osu \(z\)) totiž nejsou geodetiky Flammova paraboloidu (jak si můžete vyzkoušet sami pomocí reálného modelu nebo zmíněného appletu).
Důsledkem absence časové složky je, že umístíme-li na plochu pomyslně těleso s nulovou počáteční rychlostí, nemá se důvod začít hýbat. Opět nám tu nefunguje volný pád, protože se gravitaci snažíme reprezentovat přímo zakřivením plochy, ale to je pouze prostorové, nikoli prostoročasové. Do toho vstupuje další komplikace. V případě reálné demonstrace typicky používáme plochu jako trychtýř a vysílané kuličky jsou kromě zakřivení plochy ovlivňovány i skutečnou gravitací. Ta je tam ale navíc a dále vychyluje pohyb kuliček. Na druhou stranu, díky působení skutečné gravitace na našem modelu vlastně nakonec ukázka volného pádu funguje, protože kuličky přirozeně kloužou do středu plochy. Dá se tedy říci, že díky působení skutečné gravitace se posílání kuliček po ploše kvalitativně více blíží skutečnému pohybu ve sféricky symetrickém gravitačním poli, kde se podle OTR tělesa pohybují po geodetikách v prostoročase, než třeba když vizualizujeme geodetický pohyb na Flammově paraboloidu.
Viděli jsme způsob, jak můžeme vizualizovat prostorové zakřivení (byť zjednodušené do jedné roviny) předpovídané obecnou relativitou. Vizualizovat časovou část zakřivení, či lépe plné prostoročasové zakřivení je ale výrazně komplikovanější. Přesto jisté omezené možnosti existují. My to sice v našem povídání nebudeme dále potřebovat, ale trochu více se o této problematice můžete dozvědět v tomto videu. My se nyní podobně jako v předchozí kapitole po hrátkách s prostorovou křivostí podíváme na zoubek času.
Gravitační dilatace času podruhé
Nyní jsme již dostatečně vybaveni k tomu, abychom si o gravitační dilataci času i něco spočítali. Vzpomeňme nejprve na rovnici \eqref{4.24} vyjadřující vztah mezi plynutím vlastního času pozorovatele stojícího na konstantním \(r\) a souřadnicového času \(t\). Ten, jak už víme, má význam vlastního času statického pozorovatele v nekonečnu. Význam času \(t\) spočívá v tom, že se na něm všichni v daném gravitačním poli shodnou, respektive si ho dokáží dopočítat. Dá se tedy použít jako takový překladač. Představme si, že máme dva statické pozorovatele, říkejme jim Adéla a Bedřich, stojící na konstantních souřadnicích \(r_A\) a \(r_B\). Pro oba musí platit rovnice \eqref{4.24}, jen s jinou radiální souřadnicí: \begin{equation*} d\tau_{A,B}=\sqrt{1-\frac{r_\text{S}}{r_{A,B}}}\text{d}t\implies \text{d}t=\frac{\text{d}\tau_{A,B}}{\sqrt{1-\frac{r_\text{S}}{r_{A,B}}}}, \end{equation*} kde jsme jen použili zavedené označení pro Schwarzschildův poloměr a samozřejmě v našem úsporném značení platí vždy buď index A nebo B. Protože v obou vztazích vystupuje stejný přírůstek souřadnicového času \(\text{d}t\), může vyjádřit vztah mezi přírůstky vlastních časů obou pozorovatelů \begin{equation*}\tag{4.28}\label{4.28} \frac{\text{d}\tau_A}{\sqrt{1-\frac{r_\text{S}}{r_A}}}=\frac{\text{d}\tau_\text{B}}{\sqrt{1-\frac{r_\text{S}}{r_B}}}\implies \frac{\text{d}\tau_A}{\text{d}\tau_B}=\frac{\sqrt{1-\frac{r_\text{S}}{r_A}}}{\sqrt{1-\frac{r_\text{S}}{r_B}}}. \end{equation*}
Poznámka 4.11
Zde je třeba jedno malé upozornění. Rovnost přírůstku souřadnicového času pro oba pozorovatele, na které je založen vztah \eqref{4.28} není zcela automatická. Podobně jako ve třetí části o speciální relativitě sice pro názornost mluvíme o přírůstcích (změnách) souřadnic a veličin, neměli bychom ale zapomínat, že všechny tyto změny jsou mezi nějakými událostmi. Striktně vzato, přírůstek vlastního času pozorovatele je čas, který uplyne mezi dvěma událostmi, kterým je přítomen. Uplyne-li tedy pro Adélu čas \(\text{d}\tau_\text{A}\), odpovídá to uplynutí souřadnicového času \(\text{d}t_\text{A}\) podle vzorce \eqref{4.24}, a tyto časy jsou mezi dvěma konkrétními událostmi, ale jeden čas je z hlediska Adély a druhý z hlediska pozorovatele velmi daleko. Stejný argument platí pro Bedřicha, uplynutí jeho vlastního času \(\text{d}\tau_\text{B}\) odpovídá souřadnicový \(\text{d}t_\text{B}\). Není ale možné, aby dvojice událostí pro Adélu byla stejná jako pro Bedřicha, protože pozorovatelé nejsou na stejném místě. Názorněji řečeno, hledáme odpověď typu „když pro Agátu uplyne \(10\) sekund, pro Bedřicha uplyne pouze \(7\) sekund“, ale tyto časové intervaly nejsou mezi stejnými událostmi. Například může Adéla vyslat Bedřichovi dva světelné signály. Mezi odesláním první a druhého signálu pro ni uplyne nějaké množství jejího vlastního času, označme ho také \(\text{d}\tau_\text{A}\). Bedřich oba signály zachytí podle svých hodin s časovým rozestupem \(\text{d}\tau_\text{B}\). Pokud by vůči sobě byli v klidu někde ve vesmíru daleko od zdrojů gravitační pole, \(\text{d}\tau_\text{A}\) a \(\text{d}\tau_\text{B}\) by měly být stejné. Pokud by stáli v různých místech gravitačního pole, obecně tyto intervaly stejné nebudou. A i když nejsou mezi stejnými událostmi (dvě odeslání signálu vs. dvě přijetí), přesto je díky metrice \eqref{4.22} můžeme porovnávat přes souřadnicový čas \(t\).
V odvození vztahu \eqref{4.28} využíváme statičnosti Schwarzschildova řešení, což znamená, že v metrice \eqref{4.22} žádný metrický koeficient nezávisí explicitně na čase. Jakkoli je tedy geometrie prostoročasu kolem nerotujícího sférického tělesa zakřivená, toto zakřivení se s časem nemění (což dává smysl, protože samotné těleso zakřivující prostoročas se nijak nemění). Důsledkem je, že oba signály vyslané Adélou letí k Bedřichovi stejnou dobu, takže naše přímé porovnání jejich vlastních časů takto dává smysl. Pointa této poznámky tedy je, že pro složitější prostoročasy (např. okolo nesymetrického rotujícího tělesa) možné, že by se zmíněné souřadnicové časy \(\text{d}t_A\) a \(\text{d}t_B\) mohly obecně lišit a náš přímočarý postup by nefungoval.
Rovnice \eqref{4.28} nám tedy umožňuje (plně v relativistickém duchu) porovnat plynutí času dvou stojících pozorovatelů. Protože ve vztahu jsou samé konstanty a protože je Schwarzschildova metrika statická (vizte poznámku 4.11), platí tento vztah nejenom pro infinitezimální časové přírůstky, ale obecně i pro konečné časy. Zkusme si rychlý odhad. Dejme tomu, že Adéla stojí na Zemi v oblasti rovníku (tj. její radiální souřadnice bude mít hodnotu rovníkového poloměru Země). Sice víme, že souřadnice \(r\) nemá správně vzato význam vzdálenosti od středu, ale v případě slabého gravitačního p ,0ole, jako máme na Zemi, je rozdíl zanedbatelný. Také si můžeme vzpomenout, že Schwarzschildův poloměr pro Zemi je necelých \(9\:\text{mm},\) ale na povrchu se nacházíme zhruba \(6378\:\text{km}\) od středu, tedy asi \(709\) milionkrát dále než je \(r_\text{S}\). Gravitační natažení délek nám tedy nyní nemusí komplikovat situaci. Bedřich bude stát na střeše budovy o výšce \(50\:\text{m}\), jeho radiální souřadnice tedy bude o těchto \(50\:\text{m}\) větší. Po dosazení do \eqref{4.28} dostáváme výsledek přibližně \(0,9999999999999946\). Pokud by neexistovala gravitační dilatace času, výsledek by samozřejmě měl být rovný jedné. Vidíme, že je o něco málo menší, i když se od jedničky liší až na 15. desetinném místě. Výsledek menší než jedna znamená, že \(\text{d}\tau_A\) je o trochu menší než \(\text{d}\tau_B\). Zjednodušeně řečeno, zatímco Bedřichovi uplyne nějaký daný čas, třeba \(10\:\text{s}\), Adéle, která je níže v gravitačním poli uplyne pouze \(9,999999999999946\:\text{s}\). Její čas je tedy oproti Bedřichovi zpomalený, uplyne ho méně. Případně naopak, Bedřichův čas je oproti Adéle zrychlený. Tento výsledek potvrzuje náš dřívější závěr z prvních úvah o gravitační dilataci času. V místech se silnějším gravitačním polem plyne čas pomaleji.
Zmiňme si jeden zajímavý experiment, který měl tuto hypotézu potvrdit. Jmenuje se Hafeleův-Keatingův experiment podle amerických vědců Josepha Hafeleho a Richarda Keating, kteří jej provedli v roce 1971. Vzali několik velmi přesných atomových hodin na bázi cesia do letadla a obletěli s nimi svět směrem na východ a pak na západ. Čas uplynulý na hodinách byl po každém letu porovnán s atomovými hodinami, které zůstaly na zemi. V tabulce vidíme data převzatá ze stránky Wikipedie věnované tomuto experimentu:
| Tabulka 4.7 Naměřená data Hafeleova-Keatingova experimentu, zdroj: Wikipedia | ||||
|---|---|---|---|---|
| Předpovězený rozdíl v \(\text{ns}\) | ||||
| Gravitační efekt | Kinematický efekt | Celkem | Naměřeno / \(\text{ns}\) | |
| Východní směr | \(+144±14\) | \(-184±18\) | \(-40±23\) | \(-59±10\) |
| Západní směr | \(+179±18\) | \(+96±10\) | \(+275±21\) | \(+273±7\) |
V tabulce si můžeme všimnout hned několika zajímavostí. Za prvé se během experimentu uplatňuje nejen gravitační dilatace času, ale i ta kinematická, tj. ta způsobená vzájemným pohybem, kterou jsme se zabývali ve speciální relativitě. Letadla byla pochopitelně nejenom v jiné nadmořské výšce, ale také se musela nutně vůči hodinám na zemi pohybovat. Obě dilatace samozřejmě ovlivňují chod hodin najednou, ale v přímém měření je nedokážeme nijak rozlišit. V tabulce vidíme, že autoři experimentu odhadli z teorie velikost obou efektů a pak jejich vliv sečetli. Všimněme si také, že zatímco gravitační efekt je pro oba směry letu podobný a souvisí s nadmořskou výškou letů, kinematický efekt se výrazně liší. Je to dáno skládáním rychlostí, protože nezapomeňme, že se vše odehrálo na rotující Zemi. Letět na východ znamená letět ve směru rotace Země, takže pokud chcete obletět planetu, musíte se pohybovat rychleji, než se pohybuje povrch Země. Při cestě na západ, tedy proti směru rotace, je to prakticky naopak. Letadlo stojící na runwayi se už pohybuje společně s rotující Zemí, takže pokud letíme na západ, prakticky zpočátku jen zpomalujeme vůči povrchu. Je to podobné, jako když chcete hodit míčem ve vlaku. Házíte-li ve směru pohybu, musí se míč chvíli vůči zemi pohybovat rychleji než vlak. Hodíte-li ho proti směru pohybu, je klidně možné, že se vůči zemi bude stále pohybovat stejným směrem jako vlak, jen pomaleji, takže ho vlak předběhne. Samozřejmě je možné hodit (čí spíše už vystřelit) míč směrem proti pohybu vlaku rychleji, než se vlak pohybuje, v tom případě se bude míč pohybovat i vůči zemi na opačnou stranu.
Poslední dva sloupce tabulky ukazují porovnání předpovězených hodnot s těmi naměřenými. Dobrou shodu vidíme zejména v případě pohybu západním směrem, ale i v případě toho východního se intervaly nejistoty překrývají, což poukazuje na, sice ne příliš přesnou, ale přece jen shodu mezi teorií a experimentem. Od té doby se uskutečnilo hned několik dalších podobných experimentů, které také potvrdily správnost relativistických predikcí se stále větší přesností.
Poznamenejme na téma experimentů ještě jednu zajímavost. Doba od Hafeleova-Keatingova experimentu pokročila a s ní i přesnost, které atomové hodiny dosahují. V roce 2010 se týmu z amerického Institutu standardů a technologií podařilo s využitím nové generace atomových hodin využívajících ionty hliníku (s přesností řádu \(10^{-17}\), to mimo jiné znamená, že tyto hodiny se díky akumulující se chybě „rozejdou“ o \(1\:\text{s}\) nejdříve za \(10^{17}\:\text{s}\), což odpovídá přibližně deseti miliardám let) změřit relativistickou dilataci času u dvojice hodin, které se vůči sobě pohybovaly relativní rychlostí \(10\: \text{m/s}\) (ve skutečnosti se vůči sobě pohybovaly hliníkové ionty v hodinách, ale to je jen technický detail), případně které dělila vertikální vzdálenost \(33\:\text{cm}\). A naměřené hodnoty byly opět ve shodě s relativistickou předpovědí. Odkaz na původní vědecký článek můžete najít v seznamu literatury pod [vii]. Dnes už tedy dokážeme naměřit relativistické jevy v situacích, které běžně zažíváme, nejen při pohybu rychlostí blízkou rychlosti světla nebo v okolí neutronových hvězd či černých děr. Můžete tedy směle tvrdit, že z fyzikálního hlediska je vaše hlava starší než vaše nohy.
Systémy globální satelitní navigace
Většina vědců nerada slyší, když se zeptáte, k čemu je to jejich zkoumání dobré. Richard Feynman, slavný fyzik 20. století údajně řekl, že „Fyzika je jako sex. Může přinést praktické výsledky, ale to není důvod, proč to děláme.“ Ať už s tímto bonmotem souhlasíte nebo ne, jeho poselství je asi jasné. Většina vědců zkoumá svůj obor, protože je zajímá, či ho považují za správnou cestu lidského bádání. Ne každý výzkum začne jako snaha vyřešit konkrétní problém a mnoho objevů bylo učiněno na základě čistého bádání. Přiznejme si, že dosud jsme si v našem textu neuvedli žádnou možnou odpověď na takovou všetečnou otázku o relativitě. Viděli jsme mnoho teoretických i experimentálních výsledků, ale nic využitelného v běžném životě. Nyní konečně přišla ta chvíle vytáhnout naše relativistické eso z rukávu.

Obrázek 4.40 Zjednodušený model fungování globálního satelitního navigačního systému.
Se satelitní navigací jste se již pravděpodobně setkali. Využíváme ji koneckonců všichni v našich chytrých telefonech, když chceme na mapě určit svou polohu. Způsobu, jakým telefony a jiná zařízení určují naši polohu, se někdy ne zcela správně říká GPS (z anglického Global Positioning System), ale to je ve skutečnosti název jen jednoho z několika existujících samostatných systémů. Americký GPS byl první, ale dnes existuje i ruský GLONASS, evropský Galileo nebo čínský BeiDou. Podpůrné či regionální systémy má i Japonsko (QZSS) a Indie (IRNSS). Komerční navigační zařízení ale často nejsou omezena na využívání jen jednoho z těchto systémů a běžný uživatel stejně typicky nepozná, který je jeho zařízením využíván. Souhrnně mluvíme o tzv. systémech globální satelitní navigace (GNSS – z anglického Global Navigation Satellite System, aby těch zkratek nebylo málo). Všechny jsou založeny na stejném principu. Sestávají z celé flotily satelitů obíhajících naši planetu. Každý ze satelitů má na palubě atomové hodiny a jeho úkolem je v pravidelných intervalech vysílat údaj o aktuálním čase a své poloze. Naše polohovací zařízení pak zachytí signály satelitů, které jsou „na dohled“, a z rozdílu časů mezi odesláním signálu a jeho přijetím, za předpokladu, že se signál pohybuje rychlostí světla, vypočítá vzdálenost, jakou se nacházíme od satelitu jednoduše jako \(\Delta s=c\Delta t\). Musíme se tím pádem nacházet někde na sféře o poloměru \(\Delta s\) se středem ve sdělené poloze satelitu. Abychom pak určili naši polohu, potřebujeme teoreticky informace alespoň ze tří satelitů (obrázek 4.40). Tyto tři sféry se sice mohou obecně protínat ve dvou různých bodech, ale přidá-li se informace o tom, že se nacházíme na Zemi a ne někde ve vesmíru (či na které polokouli se zrovna nacházíme), řešení je už jednoznačné. Alespoň teoreticky, prakticky jsou díky nejistotě měření vyžadovány informace z více satelitů, čímž se zvětšuje přesnost určení naší polohy. Tím ale komplikace nekončí, náš popis je samozřejmě jen velmi zjednodušenou verzí velmi sofistikovaného technického řešení. Nahlédneme-li do technicky orientovaných článků [viii,ix] či příslušné stránky Wikipedie, zjistíme, že skutečnost je daleko složitější a inženýři navrhující navigační systémy musí pracovat také s rotací Země, vlivem atmosféry na šíření signálu apod. Navíc, jak uvidíme později, pro určení polohy s přesností alespoň na metry by naše zařízení muselo umět měřit čas s přesností přinejmenším na desítky nanosekund. To ale naše mobilní a jiná navigační zařízení typicky nedokáží a musí jim být dodávána i časová informace. Máme tedy o jednu neznámou navíc, takže ve skutečnosti je vyžadován signál ne od tří ale minimálně od čtyř satelitů. My se samozřejmě do takových technických detailů pouštět nebudeme, ale je dobré si uvědomit, že skutečnost je o mnoho složitější než náš jednoduchý výklad.
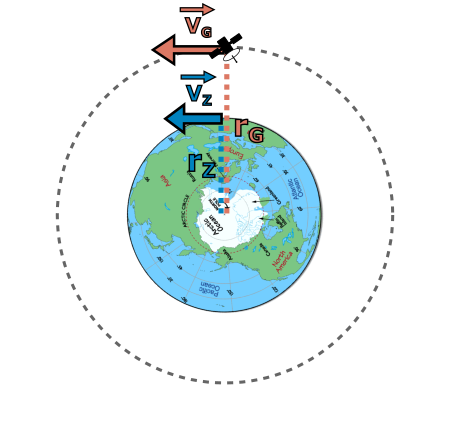
Obrázek 4.41 Náčrtek k příkladu se systémem globální navigace. Stojíme na povrchu Země v oblasti rovníku, takže se pohybuje příslušnou obvodovou rychlostí země \(\vec{v}_\text{Z}\) a naše vzdálenost od středu je samozřejmě poloměr Země \(r_\text{Z}\). Podobně navigační satelit obíhá rychlostí \(\vec{v}_\text{G}\) na kruhové dráze o poloměru \(r_\text{G}\).
Asi už chápete, kde do hry vstupuje relativita. Už jen ze vztahu \eqref{4.28} plyne, že čas na oběžné dráze satelitů plyne jinak než nám na povrchu Země, což je problém, když využíváme rozdíly časů k měření vzdálenosti. Ukažme si nyní na jednoduchém výpočtu, jaké chyby bychom se s využitím navigace dopustili, pokud bychom neznali relativitu. Vezměme si zjednodušenou situaci, kdy stojíme na rovníku a chceme porovnat chod času na našich hodinách a na hodinách umístěných v satelitu navigačního systému Galileo, který kolem Země obíhá po přibližně kruhové dráze o poloměru \(r_\text{G}\) a rychlostí \(\vec{v_\text{G}}\) (obrázek 4.41). V tomto případě ale již jistě nemůžeme použít vzorec \eqref{4.28}, protože ani my, ani satelit nejsme statičtí pozorovatelé. Jedna možnost by byla pracovat v rotující soustavě Země, ve které bychom my na povrchu byli statičtí a museli bychom pracovat jen s pohybem satelitu. Tento postup s sebou ale nese technické komplikace jako nutnost přetransformovat se do rotující soustavy apod. Jednodušší bude pracovat v nerotující soustavě spojené se středem Země, kdy budeme považovat prostoročas kolem planety za schwarzschildovský a pracovat s pohybem nás i satelitu. Další zjednodušení plyne opět z faktu, že už na povrchu Země se pohybujeme mnohonásobně dále, než je příslušný Schwarzschildův poloměr Země (cca 9 mm). V tabulkách 4.5 a 4.6 jsme ukázali, jak relativní chyba, když souřadnici \(r\) přímo ztotožníme s radiální vzdáleností, silně klesá už pro tisícinásobek \(r_\text{S}\). Jak už jsme se zmiňovali, na rovníku jsme na radiální souřadnici přibližně \(r_\text{Z}=6378000\:\text{m}=7{,}2\cdot 10^8\:r_\text{S}\), deformační efekt gravitace je tedy velmi malý. Na orbitě satelitu systému Galileo, jejíž poloměr činí přibližně \(29600\:\text{km}\), to bude samozřejmě ještě méně. Můžeme si to ověřit přímým dosazením do vzorce \eqref{4.26} pro skutečnou radiální vzdálenost. Relativní chyba, pokud bychom vzdálenost mezi povrchem Země a oběžnou drahou satelitu vypočítali přímo jako rozdíl radiálních souřadnic, činí přibližně \(0{,}0000009\:\%\). Jistě tedy neuděláme velkou chybu, když budeme ve výpočtu přímo používat radiální vzdálenosti. Za těchto i několika dalších zjednodušujících předpokladů je možné odvodit pro porovnání plynutí času na Zemi a na oběžné dráze satelitu systému Galileo \begin{equation*}\label{4.29}\tag{4.29} \frac{\text{d}\tau_\text{Z}}{\text{d}\tau_\text{G}}=\frac{\sqrt{1-\frac{r_\text{S}}{r_\text{Z}} -\frac{v_\text{Z}^2}{c^2}}}{\sqrt{1-\frac{r_\text{S}}{r_\text{G}}-\frac{v_\text{G}^2}{c^2}}}. \end{equation*}
Pro jakéhokoli pozorovatele vykonávajícího kruhový pohyb platí \(\text{d}r=0\), a tím pádem dostáváme pro jejich vlastní čas z definice \begin{equation*} \text{d}\tau=\frac{\sqrt{-(\text{d}s)^2}}{c}=\frac{\sqrt{c^2\left(1-\frac{r_\text{S}}{r}\right)(\text{d}t)^2-r^2(\text{d}\varphi)^2}}{c}=\frac{c\text{d}t\sqrt{\left(1-\frac{r_\text{S}}{r}\right)-\frac{r^2}{c^2}\frac{(\text{d}\varphi)^2}{(\text{d}t)^2}}}{c}. \end{equation*} V poslední úpravě jsme před odmocninu vytknuli výraz \(c^2(\text{d}t)^2\). Zkrátíme rychlosti světla a všimněme si druhého výrazu v odmocnině. Jak už víme, součin \(r\text{d}\varphi\) vyjadřuje malé posunutí \(\text{d}o\) na obvodu kružnice o poloměru \(r\). Díky vytknutí je pod odmocninou výraz \(r^2(\text{d}\varphi)^2/(\text{dt})^2=(r\text{d}\varphi/\text{d}t)^2=(\text{d}o/\text{d}t)^2\). Jedná se tedy o tečnou vzdálenost, o kterou se pozorovatel posune na obvodu za souřadnicový čas \(\text{d}t\). Protože pracujeme v infinitezimálních posunutích, můžeme malý oblouk do považovat za úsečku, takže v závorce je přímo kruhová rychlost pozorovatele. Ale pozor, je důležité si uvědomit, že se nejedná o kruhovou rychlost, kterou si sám naměří obíhající pozorovatel (vzhledem ke svému okolí), to by ve vztahu muselo být \(\text{d}o/\text{d}\tau\), tedy změna vzdálenosti za jeho vlastní čas (připomeňme, že vzdálenost v tečném směru do je pro všechny zúčastněné pozorovatele stejná). Je to rychlost, kterou naměří pozorovatel v nekonečnu. Zlomek můžeme ale upravit následujícím způsobem (technicky vzato zde používáme pravidlo o derivaci vnitřní funkce): \begin{equation*} \left(\frac{\text{d}o}{\text{d}t}\right)^2=\left(\frac{\text{d}o}{\text{d}\tau}\frac{\text{d}\tau}{\text{d}t}\right)^2=\left(\frac{\text{d}o}{\text{d}\tau}\right)^2\left(\frac{\text{d}\tau}{\text{d}t}\right)^2=\left(\frac{\text{d}o}{\text{d}\tau}\right)^2\left(1-\frac{r_\text{S}}{r}\right). \end{equation*} Označme si vlastní kruhovou rychlost \(\text{d}o/\text{d}\tau\) jako \(v\). Pro vlastní čas potom dostáváme \begin{equation*} \text{d}\tau=\text{d}t\sqrt{1-\frac{r_\text{S}}{r}-\frac{v^2}{c^2}\left(1-\frac{r_\text{S}}{r}\right)}. \end{equation*} Dovolíme si ještě jedno zjednodušení. Jelikož se pohybujeme ve slabém gravitačním poli, bude zlomek \(r_\text{S}/r\) poměrně malý. V případě povrchu Země vychází přibližně \(1{,}4\cdot 10^{-9}\). Podobně poměr kruhové rychlosti a rychlosti světla bude dost malý. Rychlost satelitu, který je z obou uvažovaných situací rychlejší, můžeme buďto najít na internetu nebo odhadnout ze známého klasického vztahu pro kruhovou rychlost potřebnou pro obíhání tělesa o hmotnosti \(M\) na vzdálenosti \(r\): \(v=\sqrt{GM/r}=3675\:\text{m/s}\) (opět zde využíváme, že ve slabém gravitačním poli kolem Země platí pro kruhovou rychlost klasické vztahy, o vztahu a mezích platnosti relativistické a klasické teorie gravitace se ještě zmíníme). Pro tuto rychlost vychází \(v^2/c^2\doteq 1{,}5\cdot 10^{-10}\). Vidíme tedy, že násobením těchto dvou čísel dostáváme číslo ještě výrazně menší než ostatní členy v odmocnině, a proto můžeme prakticky poslední závorku nahradit jedničkou. Když potom budeme, podobně jako v předchozím, porovnávat plynutí času na Zemi a na oběžné dráze satelitu systému Galileo, dostáváme výraz (4.29): \begin{equation*} \frac{\text{d}\tau_\text{Z}}{\text{d}\tau_\text{G}}=\frac{\sqrt{1-\frac{r_\text{S}}{r_\text{Z}} -\frac{v_\text{Z}^2}{c^2}}}{\sqrt{1-\frac{r_\text{S}}{r_\text{G}}-\frac{v_\text{G}^2}{c^2}}}. \end{equation*} Ve vztahu jsme opět zkrátili ve zlomku \(\text{d}t\), přičemž platí stejné argumenty, které jsme uvedli už dříve u porovnání časů statických pozorovatelů.
Odvozený výraz není o moc složitější než ve statické situaci a hlavně poměrně hezky ilustruje oba zdroje dilatace času. Zatímco první dva členy pod odmocninami představují statickou situaci, kterou už známe, první a třetí člen nám zase dávají vzpomenout na speciální relativitu a výrazy typu \(\sqrt{1-v^2/c^2}\). Vidíme tak jednoduchou ilustraci toho, že obecná relativita v sobě tu speciální zahrnuje, není od ní oddělena, je spíš její nadmnožinou či zobecněním. Na rozdíl od pánů Hafeleho a Keatinga zde tedy nemusíme gravitační a kinematický příspěvky k dilataci času sčítat, ale máme přímo jeden vzorec (ale abychom si zase příliš nefandili, my jsme tento vzorec odvodili za velmi specifických zjednodušujících podmínek pohybu po kružnici, oni měli situaci výrazně komplikovanější).
Konečně můžeme do našeho vztahu dosadit. Respektive ho využijeme, abychom spočítali relativní odchylku časů uplynulých pro nás na povrchu Země a pro satelit: \begin{align*} \frac{\text{d}\tau_\text{G}-\text{d}\tau_\text{Z}}{\text{d}\tau_\text{G}}=1-\frac{\text{d}\tau_\text{Z}}{\text{d}\tau_\text{G}}=1-\frac{\sqrt{1-\frac{r_\text{S}}{r_\text{Z}}-\frac{v_\text{Z}^2}{c^2}}}{\sqrt{1-\frac{r_\text{S}}{r_\text{G}}-\frac{v_\text{G}^2}{c^2}}}=1-\frac{\sqrt{1-\frac{8{,}8\cdot10^{-3}}{6378\cdot10^3}-\frac{464^2}{9\cdot10^{16}}}}{\sqrt{1-\frac{8{,}8\cdot10^{-3}}{29600\cdot10^3}-\frac{3675^2}{9\cdot10^{16}}}}\dot{=}\:4{,}67\cdot10^{-10} \end{align*} Tento výsledek znamená, že zatímco hodinám v satelitu uplyne \(1\) sekunda, na Zemi nám uplyne o zhruba půl nanosekundy méně. Nezdá se to jako moc, ale je to již měřitelný rozdíl. Předně si ale musíme uvědomit, že tato nepřesnost se s každou sekundou kumuluje. Za celý den činí časový rozdíl asi \(40\) mikrosekund. Když si pak vzpomeneme, že navigační systém pomocí rozdílu časů vyslání a přijetí určuje naši vzdálenost od satelitu, odpovídá to přibližně chybě v určení vzdálenosti \(\Delta s=c\Delta t=3\cdot 10^8\cdot40\cdot 10^{-6}\:\text{m}=12000\:\text{m}\). Pokud bychom neznali relativitu, systém globální navigace by se za jeden den rozešel s realitou o \(12\:\text{km}\) při určování vzdálenosti od nás k satelitům, a tím pádem by vznikla chyba i v určení naší polohy. Relativistické efekty jsou tedy v okolí Země sice malé, ale satelitní navigační systémy musí měřit čas s takovou přesností, že se zde relativita již jasně projevuje.
Traduje se, že když byl ve Spojených státech v 70. letech minulého století vyvíjen systém GPS, byla sice už teorie relativity fyzikům známa, ale inženýři navrhující systém v ní neměli velkou důvěru. Proto byly sice do satelitů naprogramovány potřebné relativistické korekce, ale byly zpočátku vypnuty s možností je dálkově zapnout. Po úvodním spuštění začala přesnost systému postupně degradovat, což napravilo až zapnutí zabudovaných korekcí. Až se vás tedy někdy někdo zeptá, k čemu je ta relativita vlastně dobrá, zeptejte se jich na oplátku, kdy naposled používali mapy s globální navigací.
Orbity a stáčení perihelia
Zatím jsme si rozebrali různé speciální případy, jednak abychom ukázali konkrétní relativistický jev a jednak, protože se nám řešily výrazně jednodušeji než obecný matematický popis. S výkladem klasické gravitace na střední škole je to ale dost podobné. Typickým průběhem je, že si ukážeme Newtonův gravitační zákon a aplikujeme ho na několik jednoduchých případů jako je kruhová orbita nebo úniková rychlost (v lepším případě se dozvíme i něco o Keplerových zákonech, které popisují zákonitosti obíhání planet kolem Slunce a z nichž Newton odvodil svůj gravitační zákon). Nikdy ale neřešíme obecnou úlohu, jak se bude dané těleso pohybovat kolem centrálního tělesa, pokud známe jeho počáteční polohu a rychlost (tzv. Keplerova úloha nebo také speciální případ problému dvou těles, kdy jedno z dvojice gravitačně působících těles je výrazně hmotnější – například hvězda a planeta). Důvodem je, že sice umíme v každém okamžiku spočítat sílu (potažmo zrychlení) tělesa, ale protože se díky změně polohy tělesa síla neustále mění, neumíme pomocí středoškolské matematiky dopočítat, jak se mění rychlost a poloha.
Poznámka 4.12
Video 4.42 Applet počítající dráhu objektu pomocí okamžitého zrychlení (zelená šipka) a následného dopočtu okamžité rychlosti (červená šipka) a polohy v mnoha po sobě jdoucích diskrétních krocích.
Můžeme ale například využít appletů, které tento problém umí vyřešit za nás. Na videu 4.42 vidíme applet, který po zadání počátečních podmínek (tj. polohy a rychlosti tělesa) dopočítává trajektorii oběhu kolem centrálního tělesa. Jedná se tzv. numerické řešení (či numerické modelování), kdy místo abychom daný problém vyřešili analyticky (tj. odvodili vzoreček), necháme počítač, aby pracoval za nás. V této poměrně jednoduché aplikaci to znamená, že v daném okamžiku počítač vypočítá podle zadaného vzorce zrychlení tělesa, načež dopočítá, jak se kvůli tomu změní rychlost a poloha tělesa, a celá situace se o malý časový krok posune. Znovu vypočítá zrychlení (dané v gravitačním poli zejména polohou) obíhajícího tělesa a ostatní veličiny a znovu ho posune. Prakticky tak nahrazujeme plynulý pohyb velkým množstvím po sobě jdoucích statických situací, stejně jako statická políčka jdoucí rychle po sobě tvoří film. Počítač tedy vlastně neví, jak se bude situace vyvíjet dlouho dopředu, má od nás pouze návod, jak se posunout od jednoho „okamžiku“ ke druhému. Je asi zřejmé, že zvolená velikost časového kroku silně ovlivňuje přesnost takových výpočtů, ale to není všechno. Jak už to tak bývá, je zde samozřejmě celá řada technických obtíží jak zajistit, aby naše výpočty byly rozumné a co nejpřesnější, respektive co nejvíce odpovídající realitě. Numerické modelování je tím pádem celý vědní obor, který prakticky už od příchodu počítačů slouží například k testování různých technických řešení (jako třeba vliv tvaru vozu na jeho aerodynamiku) aniž bychom je museli skutečně postavit.
V mnoha vědních oborech je modelování zásadním výzkumným nástrojem. Příkladem je i právě obecná relativita, protože její matematický popis je natolik složitý, že často ani není možné odvodit řešení daného problému algebraicky, a tak nám zbývá pouze numerická cesta. Jelikož už víme, že podle relativity se tělesa pohybují v zakřiveném prostoročase po geodetikách, z matematického hlediska je řešení pohybu tělesa vlastně „jen“ hledáním geodetiky. Ve zjednodušené míře jsme už něco takového také viděli. Ve videích 4.9 až 4.13 byly momentky z appletů, které vypočítávali geodetický pohyb bodů (kuliček) po sféře. Pohyb kuliček po sféře jsme modelovaly pomocí tzv. rovnice geodetiky. Ve zkratce se jedná o matematickou rovnici, jejíž tvar plyne z metriky a která určuje, jak se mění směr a rychlost pohybu na zakřivené ploše pomocí křivosti v daném místě. Vyřešit rovnici geodetiky by znamenalo získat explicitní pohybové rovnice, tj. takové, pomocí kterých bychom v libovolném čase mohli přímo dopočítat polohu a rychlost bodu. Nicméně i v tak poměrně jednoduchém případě sféry, kdy tvar geodetik vlastně známe předem (jsou to části hlavních kružnic), se jedná o dost namáhavý úkol. U složitějších geometrií už to nemusí jít vůbec. Přesto ale můžeme geodetický pohyb simulovat numericky, tj. přesně v souladu s již řečeným, v každém okamžiku určit danému tělesu směr, kterým má pokračovat, aby šlo stále po geodetice. Kdykoli v tomto textu narazíte na momentku z animace bodu pohybujícího se na zakřivené ploše, uvnitř daného programu je schována rovnice geodetiky pro danou plochu, která bodu říká, jak se posunout o další malý kousek dále. A pak zase, a pak zase. Tím po kouscích složíme geodetiku jak daleko je nám libo.
V prostoročasu přibývá každému tělesu ještě časová souřadnice. Těleso se tedy pohybuje prostorem i časem (tj. plyne mu čas) a tyto dva „pohyby“ jsou spolu provázány. Již jsme viděli příklad s volným pádem, kdy čistě existence tělesa (= pohyb v čase) v zakřiveném prostoročase (= gravitačním poli) způsobí i změnu prostorové polohy tělesa. Řešení rovnice geodetiky nám tedy může říct nejen, jak se těleso bude pohybovat, jinými slovy jak se mu budou měnit prostorové souřadnice, ale i jak mu bude plynout čas (změna časové souřadnice). V tomto textu se nebudeme věnovat konkrétním příkladům rovnice geodetiky ani jejich řešení, protože je to i pro velmi jednoduché plochy pro nás matematicky příliš komplikované, natož pro Schwarzschildův prostoročas. Snažíme se tu ale alespoň ozřejmit podstatu věci, která navzdory složitosti technických detailů zas tak komplikovaná není.
Jednou ze základních předpovědí problému dvou těles v klasické gravitaci je, že má-li například planeta obíhat hvězdu, bude obecně obíhat po elipse (připomeňme, že kružnice je speciální případ elipsy) a tato elipsa je pevná v prostoru. Už víme, že kolem sféricky symetrického centrálního tělesa bude tento oběh stále v jedné rovině, ale navíc i v rámci této roviny bude elipsa neměnná (vyzkoušet si to můžete sami v appletu). Tomu odpovídá i 1. Keplerův zákon, který (spolu s dvěma dalšími) vyslovil německý astronom Johannes Kepler na základě astronomických pozorování pohybů planet (je zajímavé, že první dva ze svých zákonů Kepler zformuloval při svém působení v Praze na dvoře Rudolfa II). Podle něj se planety pohybují kolem Slunce po eliptických drahách blízkých kružnici. Tvar drah planet je nám tedy znám již od začátku 17. století. Po více jak dvě století byla skutečnost, že Newtonův gravitační zákon velmi dobře funguje pro vysvětlení pohybů těles v naší sluneční soustavě brán jako zřejmý důkaz správnosti klasické teorie gravitace. Nejenom, že dokázala vysvětlit dráhy známých astronomických těles, ale byla také využita k objevení nové planety. Po objevení Uranu ve druhé polovině 18. století bylo pozorováno, že jeho dráha není přímo taková, jaká by podle výpočtů měla být. Jako by za Uran „něco tahalo“. Byla tak předpovězena existence další planety, a její poloha i hmotnost byly předem spočítány. V roce 1846 tak byl objeven Neptun pomocí dalekohledů namířených do míst, která předpověděla Newtonova teorie.
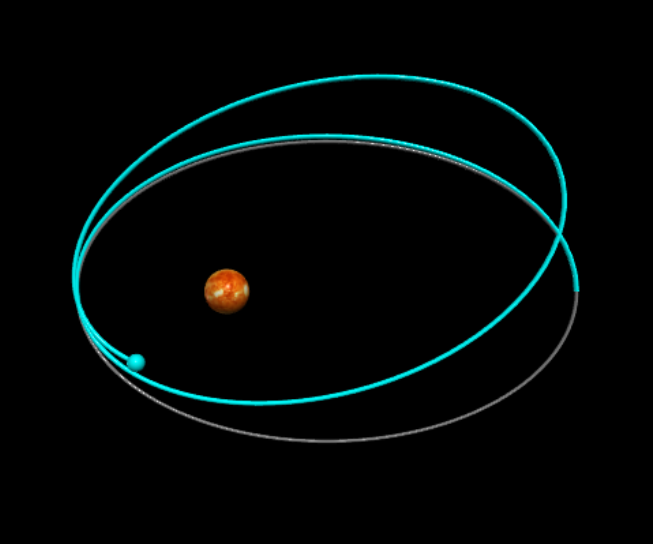
Obrázek 4.43 Ilustrace stáčení trajektorie planety v rovině oběhu. Efekt je pro lepší přehlednost silně přehnaný.
Jak se ale astronomická měření zpřesňovala, bylo zjištěno, že eliptická dráha Merkuru není tak neměnná, jak předpovídá problém dvou těles. Dochází u něj k tzv. stáčení perihelia. Perihelium (česky přísluní) nazýváme bod na trajektorii tělesa obíhající Slunce, kdy je těleso Slunci nejblíže (nejvzdálenější bod se nazývá afélium neboli odsluní). Stáčením perihelia máme na mysli, že obíhající těleso ve skutečnosti svou trajektorii přesně neuzavírá, čímž se pomyslná elipsa oběhu otáčí ve směru obíhání (obrázek 4.43). Nestáčí se tedy jen perihelium, je to pouze zjednodušené pojmenování stáčení celé trajektorie. Tento jev je sice možné vysvětlit tím, že na Merkur kromě Slunce působí i další planety, takže ho vychylují z předpovězené přesně eliptické dráhy, z výpočtů se ale ukázalo, že vlivem ostatních planet dokážeme vysvětlit většinu stáčení, ale ne všechno. Jako možné vysvětlení se spekulovalo o existenci další, do té doby neznámé planety (byla pojmenována Vulkán), která by hypoteticky obíhala blíže Slunci než Merkur (což by vysvětlovalo, obtížnost jejího pozorování). Nikdy ale nebyla pozorována a zejména na základě neúspěšných hledání při zatměních Slunce mezi lety 1883 a 1908 bylo nakonec od pátrání upuštěno.
Poznámka 4.13
Dovolme si rychlou odbočku o názvosloví. V astronomii se názvy perihelium a afélium používají jen u těles obíhajících Slunce (v obou slovech tušíme jako součást Hélios – jméno řeckého boha Slunce). Obecně se tyto dva význačné body na eliptické dráze tělesa nazývají apsidy. Máme tak apoapsidu (také nazývanou apofokus) a periapsidu (perifokus). Aby toho nebylo málo, můžeme se setkat i s verzemi pericentrum a apocentrum, které jsou vztaženy ne vůči centrálnímu tělesu, ale vůči těžišti soustavy.
A aby to bylo ještě zajímavější, typicky se apsidy pojmenovávají podle konkrétního centrálního tělesa. Například při oběhu Země mluvíme o apogeu a perigeu (s hezkými českými překlady odzemí a přízemí). Exoplaneta obíhající kolem nějaké cizí hvězdy prochází skrz periastron a apoastron. Naše sluneční soustava na své cestě kolem galaktického jádra zase projde svým perigalaktikem a apogalaktikem atd. My si naštěstí vystačíme jen s periheliem.
Pojďme se podívat na konkrétní data. V tabulce 4.8, převzaté z Wikipedie a následně upravené, je dole uvedena naměřená hodnota stočení trajektorie Merkuru přibližně \(574\) úhlových sekund za století. Uvědomme si, jak malá je to hodnota. Jeden úhlový stupeň dělíme na \(3600\) úhlových sekund, takže se jedná o stočení přibližně o \(1/7\) stupně za \(100\) let. Je až neuvěřitelné, s jakou přesností musela být tato pozorování provedena. V tabulce je také vypsáno několik různých jevů přispívajících ke stáčení Merkuru a teoretické předpovědi jejich velikosti.
| Tabulka 4.8 Data ke stáčení perihelia Merkuru, zdroj: Wikipedia | |
|---|---|
| Úhlové sekundy za století | |
| Vliv ostatních těles Sluneční soustavy | \(532{,}3035\) |
| Zploštění Slunce | \(0{,}0286\) |
| Rotace Slunce | \(-0{,}0020\) |
| Schwarschildovský efekt | \(42{,}9799\) |
| Celkem předpovězeno | \(575{,}31\) |
| Pozorováno | \(574{,}10±0{,}65\) |
Z tabulky vidíme, že klasická teorie gravitace dokáže díky působení dalších těles vysvětlit téměř \(93 \%\) stáčení. Jsou zde uvedeny i další minoritní jevy související s ne zcela kulovým tvarem Slunce a jeho rotací (tedy jevy nad rámec Schwarzschildova řešení), jejich vliv je ale relativně malý. Pro nás je důležitý další řádek. Ukazuje se totiž, že obíhá-li těleso ve Schwarzschildově prostoročasu, efekt stáčení orbity je přítomen rovnou. V [5] můžeme najít odvození přibližného vztahu pro úhel stočení trajektorie planety po jednom oběhu: \begin{equation*}\label{4.30}\tag{4.30} \Delta\varphi=\frac{6\pi GM}{c^2a\left(1-e^2\right)}, \end{equation*} kde \(a\) je tzv. hlavní poloosa a \(e\) numerická excentricita, což jsou dva z geometrických parametrů popisujících elipsu a pro každou planetu naší soustavy jsou dobře známy. I když jejich přesný význam není pro nás tolik podstatný, pro lepší představu ho můžeme vidět na obrázku 4.44, který jsme si vypůjčili z Wikipedie.
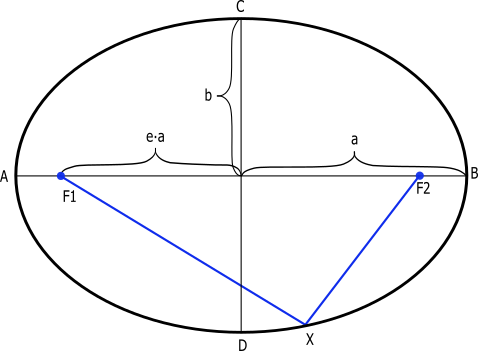
Obrázek 4.44 Nahoře: Parametry popisující elipsu. Hlavní poloosa \(a\) je polovina delšího rozměru elipsy, numerická excentricita \(e\) je poměr vzdálenosti ohnisek od středu a hlavní poloosy. Pro elipsy platí \(e\lt 1\) a v případě, kdy se rovná \(0\), dostáváme kružnici.
Zkusme nyní do vztahu dosadit pro Merkur. Jeho orbitální parametry můžeme snadno najít a význam ostatních konstant již známe. \begin{equation*} \Delta\varphi=\frac{6\pi\:6{,}67\cdot10^{-11}\cdot1{,}989\cdot10^{30}}{9\cdot10^{16}\:57{,}909\cdot10^9\left(1-0{,}2056^2\right)}\dot{=}\:5{,}02\cdot10^{-7}. \end{equation*} Vyšlé číslo nám patrně nic neříká. Musíme si totiž uvědomit, co jsme vypočítali. Stočení perihelia Merkuru za jeden jeho oběh v radiánech. Abychom náš výsledek mohli porovnat s hodnotou v tabulce 4.8, budeme ho muset trochu upravit. Předně ho musíme vydělit periodou oběhu Merkuru, která činí přibližně \(87{,}97\) dne. Tím dostaneme úhlové posunutí za jeden den, odtud už snadno převedeme na posunutí za sto let. V poslední řadě převedeme výsledek na úhlové sekundy. Abychom dostali stupně, musíme hodnotu vydělit \(\pi\) a vynásobit \(180\). Úhlové sekundy pak dostaneme finálním vynásobením \(3600^{\prime\prime}\). Celkem tedy \begin{equation*} \Delta\varphi(\:{}^{\prime\prime}\:\text{za}\:100\:\text{let})=\frac{5{,}02\cdot10^{-7}\cdot365{,}25\cdot100\cdot180\cdot3600^{\prime\prime}}{87{,}97\pi}=42{,}99^{\prime\prime}. \end{equation*} Náš výsledek se neshoduje zcela přesně s hodnotou z tabulky díky použití zaokrouhlených hodnot konstant, ale je mu dostatečně podobný na to, abychom mohli výpočet považovat za správný. Když byla díky obecné relativitě správně předpovězena velikost chybějícího dílu stáčení dráhy Merkuru, znamenalo to definitivní konec pátrání po Vulkánu. Zároveň se jedná o jeden z prvních, dnes nazývaných klasických, testů OTR. Jedná se o vysvětlení tří jevů v naší sluneční soustavě, která navrhl jako testy své teorie Einstein v roce 1916. Vlastně jsme už jeden potkali, byl jím gravitační rudý posuv. Třetím je potom ohyb světelných paprsků v gravitačním poli, kterým se budeme zabývat v další podkapitole.
Merkur samozřejmě není jediná planeta, jejíž trajektorie se stáčí. Podobný efekt, byť slabší, je dnes změřen i u ostatních planet včetně Země, ale i těles mimo naši soustavu. Příkladem je binární systém pulzarů (rychle rotujících neutronových hvězd) PSR 1913+16. Ten byl objeven v roce 1974 a za tento objev a jeho následné zkoumání byla udělena i Nobelova cena za fyziku. Jedná se totiž o první objevený astronomický systém, pomocí něhož lze zkoumat gravitaci za výrazně extrémnějších podmínek, než v naší soustavě. Protože se jedná o systém dvou podobně hmotných těles, obíhají kolem společného těžiště, každé po své eliptické dráze. Pulzary ale své elipsy stáčí, a to výrazně silněji než u Merkuru - \(4{,}2°\) za rok (tj. více jak \(35 000\) krát více), což se velmi dobře shoduje s relativistickou předpovědí.
Ohyb světla a gravitační čočky
Další zajímavý jev souvisí s otázkou, zda gravitace ovlivňuje světlo. Sice jsme už narazili na frekvenční posuv světla (tzv. rudý posuv), ale ten jsme vysvětlili odlišným plynutím času v různých místech gravitačního pole, nikoli změnou světla samotného. Na základě toho, co zatím víme, není jednoduché na tuto otázku odpovědět. Z klasického hlediska, pokud gravitaci chápeme jako přitažlivou sílu mezi hmotnými tělesy, musíme nyní řešit otázku, zda má světlo nějakou hmotnost. Dnes už víme, že setrvačnou hmotnost nemá, a podle STR se tak ve vakuu pohybuje pouze svou standardní rychlostí c, ale to je známo (či obecně přijímáno) jen něco málo přes sto let, zatímco první doložené výpočty zakřivení trajektorie světla v gravitačním poli jsou již z roku 1784 (jedná se samozřejmě o výpočet založený na klasické teorii gravitace - detailnější popis najdeme například v [x]). Můžeme si ale také vzpomenout, že gravitace uděluje tělesům zrychlení bez ohledu na jejich hmotnost (závěr, který jsme učinili v kapitole 4.1). V tom případě by nevadilo, že světlo nemá klidovou hmotnost. Mohli bychom se na něj, stejně jako mnozí fyzikové v historii, zkusit dívat jako na proud částic, a tím pádem by bylo možné vypočítat, jak by se trajektorie světla v gravitačním poli mohla zakřivit. Předem ale není jasné, zda vůbec světlo na gravitaci reaguje, minimálně v klasické fyzice to z ničeho neplyne.
První jednoduchou odpověď na tuto otázku nám poskytne náš starý známý princip ekvivalence. Vžijme se opět do role dvou pozorovatelů. Jednoho v klidu vůči zemi, druhého v lokální inerciální soustavě reprezentované padajícím výtahem. Ten tentokrát opatříme vysílačem a detektorem na protilehlých stěnách (obrázek 4.45). Pro začátek si představme, že vysílač střílí kuličky či nějaké částice. Stojí-li výtah vůči zemi a „vysílač“ vystřelí kuličku, ta nedopadne do detektoru umístěného přesně na druhé straně výtahu, protože díky gravitaci její výška během letu poklesne (jedná se prakticky o vodorovný vrh). Vzdálenost, o kterou klesne, je dána gravitačním zrychlením \(g\) a časem letu kuličky \(\Delta t\) podle vzorce pro volný pád \(\Delta h=1/2g(\Delta t)^2\). Čas letu kuličky je dán počáteční (vodorovnou) rychlostí \(v\), kterou kuličku vystřelíme, a šířkou výtahu \(\Delta l\) jednoduše jako \(\Delta t=Δl/v\). Celkem tedy \begin{equation*}\tag{4.31}\label{4.31} \Delta h=\frac{g(\Delta l)^2}{2v^2}. \end{equation*} Když stejný pokus zopakujeme při volném pádu výtahu, situace dopadne jinak. Pokud bude výtah padat, budou detektor i pozorovatel uvnitř výtahu padat spolu s ním, a protože na ně působí gravitace stejně jako na kuličku, z pohledu výtahu se kulička pohybuje čistě přímočaře, takže dopadne do detektoru. Jedná se o přímou aplikaci slabého principu ekvivalence, který už známe. Pokud ale s touto úvahou úplně nesouzníte, můžete se podívat na reálnou demonstraci:
Obrázek 4.45 Vlevo: Stojí-li výtah vůči zemi a „vysílač“ vystřelí kuličku, ta nedopadne do detektoru umístěného přesně na druhé straně výtahu, protože díky gravitaci její výška během letu poklesne (jedná se prakticky o vodorovný vrh).
Vpravo: Pokud bude výtah padat, budou detektor, pozorovatel ale i vysílač a kulička padat spolu s ním, protože na ně gravitace působí stejně. Z pohledu pozorovatele se tedy kulička pohybuje rovnoměrně přímočaře a trefí detektor.
Nyní celou situaci zopakujeme, ale místo kuliček budeme vysílat světelný paprsek. Abychom zjistili, co se bude dít s paprskem v gravitačním poli, použijeme stejný postup jako dříve. Podíváme se na něj nejprve v padajícím výtahu. Protože se jedná o lokálně inerciální soustavu, kde platí zákony speciální relativity, světlo se tedy pohybuje rovnoměrně přímočaře. Z pohledu pozorovatele uvnitř výtahu se tedy paprsek přesně trefí do detektoru podobně jako kulička prvně. Zachycení paprsku detektorem je objektivní fakt, není možné, aby z pohledu jednoho pozorovatele detektor něco zachytil a z pohledu druhého ne. Paprsek tedy musí dopadnout do detektoru i z pohledu pozorovatele venku. Jenže během letu paprsku se nutně musel výtah pohnout volným pádem směrem dolů. Samozřejmě to nebude o moc, protože rychlost světla je veliká a proto přeletí výtah ve velmi malém čase, ale přesto ho nepřeletí okamžitě. Nějaká výchylka světla by měla jít naměřit. Pro pozorovatele venku je tedy paprsek zakřiven (nebo chcete-li, „padá“ v gravitačním poli). Zároveň se nejedná o rozpor se speciální relativitou, protože už víme, že pozorovatel venku je díky gravitačnímu poli neinerciální a proto se na něj nevztahuje předpoklad o přímočarém šíření světla.
Můžeme zkusit i rychlý odhad, stačí do vztahu \eqref{4.31} dosadit \(v=c\). Zvolíme-li za \(\Delta l\) například rozumnou vzdálenost \(10\:\text{m}\), dostáváme pro výšku „pádu“ paprsku \begin{equation*} \Delta h=\frac{g(\Delta l)^2}{2c^2}=\frac{10\cdot 100}{2\cdot 9\cdot 10^{16}}\:\text{m}\dot{=}̇5\cdot 10^{-15}\:\text{m}, \end{equation*} tedy vzdálenost srovnatelnou s rozměrem atomového jádra. To jistě není rozměr, který by se nám snadno měřil, a je to i přesně důvod, proč paprsky v gravitačním poli Země považujeme typicky za přímky. Chceme-li tento jev ověřit, budeme muset využít nějakou jinou situaci, pravděpodobně se silnějším gravitačním polem.
Princip ekvivalence tedy předpovídá, že směr šíření světla je v gravitačním poli ovlivněn. Stejně tak to předpovídá obecná teorie relativity, která z principu ekvivalence vychází. Konec konců, pokud je gravitace zakřivením prostoročasu, mělo by toto zakřivení ovlivnit trajektorii čehokoli, i světla. Netvrdíme ale, že světlo se v gravitačním poli zakřiví po stejné trajektorii jako třeba planeta. Už jenom proto, že účinek zakřivení geometrie prostoročasu sice nezávisí na hmotnosti daného tělesa, závisí ale na jeho rychlosti (můžeme si to představit tak, že trajektorie rychlejších těles se stihne zakřivit méně).
Jak už bylo zmíněno, zakřivení světelných paprsků v gravitačním poli je jedním z klasických testů OTR. Otázkou je, jak toto zakřivení otestovat. Je potřeba velmi silného gravitačního pole, aby se zakřivení mohlo dostatečně projevit. Místo s nejsilnějším gravitačním polem v naší soustavě, kudy zároveň může procházet světelný paprsek, je těsně při povrchu Slunce. Čistě teoreticky bychom tedy mohli ohyb paprsků pozorovat na poloze hvězd na nebi v momentě, když se nachází v těsné blízkosti slunečního kotouče. Problém je samozřejmě v tom, že v tomto okamžiku slunce naprosto přesvětlí okolní hvězdy (díváme-li se z povrchu Země na Slunce, musí být zcela jistě den). Řešením je pozorování provádět při úplném zatmění Slunce. Základní myšlenka takového experimentu je znázorněna na obrázku 4.46.
Obrázek 4.46 Nahoře: Pohled na místo na obloze v noci bez přítomnosti slunečního kotouče (1) a pohled na totéž místo v okamžiku úplného zatmění (2). Dochází-li k ohybu světelných paprsků v blízkosti slunečního povrchu, mělo by dojít ke zdánlivé změně polohy hvězd na obloze.
Dole: Průchod světelných paprsků přicházejících od vzdálených hvězd bez přítomnosti Slunce (3) a s ním (4). Ohyb paprsku směrem ke Slunci způsobí, že nové polohy hvězd na nebi jsou oproti svým původním polohám dál od překrytého slunečního kotouče o nějaký úhel \(\varphi\).
Protože astronomové dokáží poměrně přesně předpovídat časy zatmění i místa na Zemi, ze kterých bude možné vidět zatmění úplné (tj. že slunce bude na nebi zcela překryto), bylo na začátku 20. století možné předem naplánovat expedice, které měli za úkol proměřit, zda k ohybu světla opravdu dochází. Již jsme se zmínili, že za určitých předpokladů je možné odvodit ohyb světla i klasicky, ale tato předpověď se od té relativistické liší. Ze Schwarzschildovy metriky je možné odvodit vzorec pro velikost úhlu ohnutí paprsku, když prochází těsně při povrchu Slunce. Odvození, které je možné najít například v [5], zde pro jeho matematickou komplikovanost provádět nebudeme. Úhel ohybu světelného paprsku vychází \begin{equation*}\tag{4.32}\label{4.32} \varphi=\frac{4GM}{c^2R}. \end{equation*} V našem případě dosadíme za \(R\) poloměr Slunce, který činí podle NASA \(695700\:\text{km}\). Když dosadíme i všechny konstanty, dostáváme výsledek přibližně \(1{,}7\:^{"}\) (tj. úhlové sekundy, nezapomeňme, že úhel automaticky vychází v radiánech, takže je třeba výsledek převést na stupně a následně sekundy). To je sice velmi malý úhel z hlediska běžného života, ale pro astronomy je to měřitelná hodnota. Je zajímavé, že klasická předpověď vychází přesně poloviční, a to je právě to důležité na tomto experimentu, protože nám umožňuje nejenom zjistit, zda k ohybu světla dochází, ale pokud ano, může také rozlišit, která z teorií dává správnou předpověď (i když samozřejmě by nemusela mít pravdu ani jedna z nich). Pokud bychom do stejného vzorce dosadili data pro Jupiter, tj. druhý největší zdroj gravitace v naší soustavě, dostaneme výsledek přibližně \(0{,}017 "\), tedy shodou okolností stokrát menší než v případě Slunce. K pozorování u Jupiteru bychom tak sice nepotřebovali zatmění, ale případné hodnoty jsou výrazně hůře měřitelné. Mimochodem, dnes už byl naměřen ohyb světelných paprsků procházejících v blízkosti Jupiteru i dalších planet, ale to už trochu předbíháme. Zůstaňme ještě u historie.
V roce 1914 bylo vypraveno hned několik expedic z různých částí světa na poloostrov Krym, aby proměřily polohy blízkých hvězd při zatmění slunce. Bohužel to bylo právě v době vypuknutí první světové války a například výprava z Německa byla na území tehdejšího Ruského císařství zatčena pro podezření ze špionáže (sofistikované pozorovací vybavení, které měli s sebou, jim patrně ohledně takových podezření příliš nepomohlo). Nicméně ani expedice z neutrálních zemí jako třeba Argentina nebo (tehdy také ještě neutrální) Spojené státy, neměly štěstí a díky oblačnosti nebyla pozorování uskutečněna. Na jednu stranu to ale bylo dobře, protože v této době Einstein ještě neměl k dispozici finální podobu své obecné teorie relativity a jeho relativistická předpověď založená na principu ekvivalence byla poloviční oproti té pozdější založené na Schwarzschildově řešení (a tím se vlastně shodovala s klasickou předpovědí). Až později během první světové války přišel s předpovědí odpovídající vzorci \eqref{4.32}.
Další příležitostí bylo zatmění v roce 1919. Pro pozorování úplného zatmění byla britskou Královskou astronomickou společností vybrána dvě místa, město Sobral v Brazílii a Princův ostrov u západního pobřeží Afriky. Jedním z hlavních aktérů příprav byl astronom Arthur Eddington, který se následně zúčastnil výpravy na Princův ostrov a podle nějž se celá událost nazývá Eddingtonův experiment. Zatmění v roce 1919 mělo být obzvláště příhodné, protože jednak trvalo nezvykle dlouho (cca \(7\) minut) a zároveň se odehrávalo na pozadí příhodného množství hvězd souhvězdí Býka. Nebudeme zde vyprávět celý průběh expedice, ale zájemci si její příběh mohou přečíst například ve velmi čtivém původním Eddingtonově článku.
Naměřené polohy hvězd během zatmění bylo samozřejmě třeba porovnat s jejich normálními polohami. Ty musely být změřeny s dostatečným časovým odstupem od zatmění, aby byly dané hvězdy vidět na nočním nebi. Prvním důležitým závěrem bylo, že změřené polohy hvězd na nebi byly skutečně odlišné, čili skutečně dochází k ohybu světla v gravitačním poli. Druhým zjištěním pak bylo, že naměřené posunutí odpovídá relativistické předpovědi, nikoli té klasické. Celému experimentu a zejména jeho výsledku byla dopřána velká mediální pozornost. Zanedlouho se o tomto úspěchu obecné relativity psalo v novinách po celém světě (obrázek 4.46) a z Einsteina se stala celosvětově známá celebrita.

Obrázek 4.47 Ukázky novinových článků z The Times z roku 1919. Převzato z https://www.viten.no/filarkiv/general-relativity/.
Od slavného zatmění v roce 1919 jich samozřejmě proběhlo ještě mnoho, takže podobná měření mohla být dále prováděna a zpřesňována. Jak už bylo řečeno, dnes vědci měří ohyb paprsků i okolo planet jako například Jupiter. V takovém případě je již třeba měřit s přesností na téměř miliontiny úhlové sekundy. Asi není třeba dodávat, že všechny tyto experimenty dopadly v souladu s předpověďmi obecné relativity.
Účinky gravitačního pole na světelný paprsek si můžeme ukázat i přímo díky počítačové simulaci, jejíž výsledky shrnuje obrázek 4.48. Je asi jasné, že k výraznému ovlivnění dráhy světelného paprsku musí docházet až v silném gravitačním poli, tedy v místech, největšího zakřivení prostoročasu. V řeči Schwarzschildovy metriky to znamená na co nejmenší možné radiální souřadnici. Na obrázcích vidíme vykreslení drah několika paprsků, které prochází velmi blízko Schwarzschildově poloměru \(r_\text{S}\). To ale znamená, že centrální těleso by muselo být nějaký velice kompaktní objekt, jehož rozměry jsou srovnatelné s příslušným \(r_\text{S}\) (jak už bylo zmíněno, takové objekty jsou například neutronové hvězdy). Na pravém grafu je také vidět, co by se stalo, kdyby paprsek prolétal blíže, než je příslušný \(r_\text{S}\). Světlo je v takovém případě staženo do centra a již nemůže uniknout. Dotýkáme se zde tedy již tématu černých děr, jejichž „rozměry“ jsou určeny právě okolní oblastí, ze které světlo nemůže uniknout, takže Schwarzschildovým poloměrem. Nejsilnější ohyby světla nastávají právě v okolí černých děr, a jak uvidíme, jedná se o typický znak, podle kterého je možné černé díry pozorovat. Prozatím ale nechme skutečnou povahu centrálního tělesa stranou.
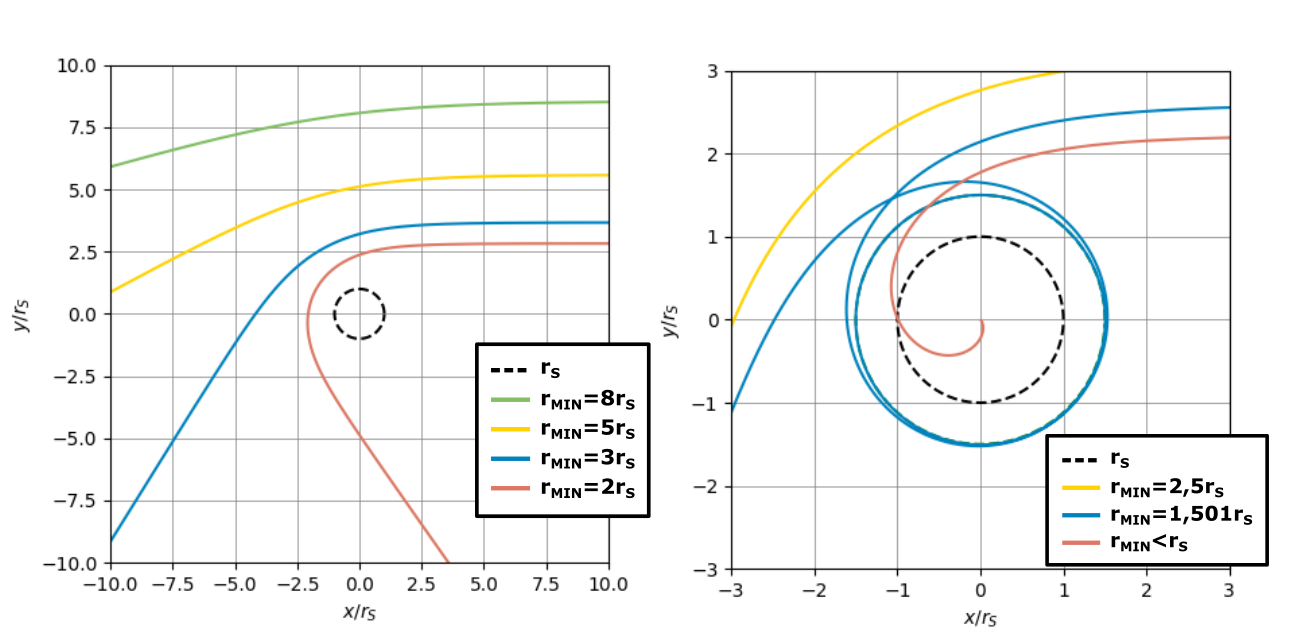
Obrázek 4.48 Dráhy světelných paprsků získané z numerické simulace. Každý paprsek je označen nejmenší radiální souřadnicí, které při svém průletu dosáhne. Pro jednoduchost zde napodobujeme polární souřadnice \(x=r\cos{\varphi}\) a \(y=r\sin{\varphi}\), čímž nedostáváme striktně vzato skutečné vzdálenosti v zakřiveném prostoročase, ale pro naši představu je to dostačující. „Vzdálenosti“ jsou vykresleny v násobcích Schwarzschildova poloměru.
Na pravé straně obrázku vidíme také velmi zajímavou situaci, kdy světlo může i obíhat kolem centrálního tělesa. Z teoretických výpočtů plyne, že na radiální souřadnici rovné \(1{,}5\:r_\text{S}\) existuje pro světlo tzv. nestabilní kruhová orbita. Slovo nestabilní v tomto případě znamená, že není možné, aby zde paprsek obíhal trvale jak planeta kolem hvězdy, dříve či později paprsek buď odletí do nekonečna, anebo „spadne“ na černou díru. Abychom situaci lépe pochopili, demonstrujme si nestabilitu na jiném příkladu. Představme si třeba, že bychom chtěli postavit vejce na špičku. Teoreticky je možné vybalancovat vejce tak, aby stálo na špičce, ale kromě toho, že je to velmi náročné na provedení, jedná se z fyzikálního hlediska o tzv. nestabilní rovnovážnou polohu, protože stačí sebemenší narušení této rovnováhy na jakoukoli stranu a vejce ze špičky spadne. Podobně i paprsek, který by se náhodou dostal na tuto kruhovou dráhu, neustále pomyslně balancuje na ostří nože, a je jen otázkou času, než se vychýlí na jednu nebo na druhou stranu. Do té doby ale může centrální těleso oběhnout i několikrát dokola.
Gravitační ohyb světla není využíván čistě jen pro ověření správnosti obecné teorie relativity. Jeho objev vedl také k novému způsobu zkoumání vesmíru – gravitačnímu čočkování. Všichni známe čočku jako průhledný předmět s dvěma vypuklými či dutými povrchy, který je typickou součástí brýlí, fotoaparátů, mikroskopů, čočkových dalekohledů apod. Fungování čočky je založeno na principu lomu světelného paprsku na rozhraní dvou různých optických prostředí. V čočce dochází ke dvěma lomům paprsku a tím k celkové změně směru světla. Díky tomu dokáže čočka vytvořit obraz, který může být například zvětšený, jako v případě lupy.
Obrázek 4.49 Náčrtek porovnávající lom světla v čočce a ohyb světla kolem například.
Díky ohybu světla může podobným způsobem fungovat i gravitace. Zásadním rozdílem ale je, že zatímco čočky lámou nejvíce světlo procházející na krajích a uprostřed prakticky ne, gravitační čočky ohýbají více světlo procházející blíže jejich středu. Typickým příkladem gravitační čočky může být galaxie nebo kupa galaxií, kolem které k nám přichází světlo ze vzdáleného zdroje. Pro pozorování tohoto efektu je tedy nutné, aby zdroj, gravitační čočka a Země ležely přibližně v jedné přímce (i když samozřejmě ne nutně ve stejném čase, protože světlo z velmi vzdálených galaxií k nám letí miliardy let). To je mimochodem důvod, proč byl sám Einstein skeptický k možnosti, že bychom tento jev někdy reálně pozorovali. Zřejmě se ale nejedná o zas tak nepravděpodobnou situaci, protože za posledních \(40\) let došlo k celé řadě pozorování. Jedním z prvních příkladů je tzv. Twin Quasar neboli dvojčatový kvazar objevený v roce 1979. Toto označení nesou dva prakticky identické kvazary zhruba \(8{,}7\) miliard světelných let daleko, které na obloze dělí asi \(6\) úhlových sekund. Z pozdějších měření vyplynulo, že se jedná o ten samý objekt, který ale vidíme dvakrát díky galaxii YGKOW G1, ležící cca \(3{,}7\) miliard světelných let daleko, ohýbající světlo (a další elektromagnetické záření) z kvazaru.
Podobných „znásobení“ objektu na obloze dnes již známe více. Konkrétní obraz pak závisí hodně na přesnosti zákrytu zobrazovaného objektu a „čočky“. Při ideálním vyrovnání se obraz objektu roztáhne do tzv. Einsteinova prstence (příklady reálných pozorování jsou na obrázku 4.50). Než abychom popisovali, jak takový prstenec (či jen jeho část) vznikne, bude jistě názornější podívat se na animaci převzatou z Wikipedie:
Jak již bylo naznačeno, gravitační čočkování neslouží pouze k ověřování správnosti obecné relativity, ale dá se ho i využít pro astronomická pozorování. Například s jeho pomocí astronomové mapují rozložení tzv. temné hmoty ve vesmíru, protože ta působí pouze gravitačně a není možné ji jinak pozorovat. Zatím jsme navíc mluvili jen o čočkování u masivních objektů jako jsou galaxie či kupy galaxií, kde je ohyb světla díky velké hmotnosti dostatečně velký a tím pádem pozorovatelný. Existuje ale i tzv. mikročočkování, ke kterému dochází při zákrytech relativně menších objektů, typicky vzdálených hvězd. V tomto případě nedochází k dostatečně silnému ohybu kolem gravitační čočky, abychom viděli více obrazů či Einsteinův prstenec, dojde ale k měřitelnému zesílení jasu předmětu (zobrazovaného tělesa) po dobu zákrytu. Pokud například tvoří čočku hvězda s planetou, může se to projevit na naměřené křivce jasu při zákrytu. Mikročočkování je tak jednou z metod, pomocí které se hledají exoplanety (tj. planety mimo naši sluneční soustavu).
Obrázek 4.50 Ukázky pozorovaných Einsteinových prstenců z Hubbleova teleskopu. Převzato z Wikipedie.
V této a několika předcházejících podkapitolách jsme se zabývali experimentální stránkou věci. Jakkoli se může zdát obecná teorie relativity zajímavou či krásnou, jako vědecká teorie musí být schopna dávat předpovědi, které je pak možné reálně otestovat. A to se OTR již více jak sto let daří takřka na výbornou. Zmínili jsme tzv. klasické testy OTR, tj. gravitační rudý posuv, stáčení perihelia Merkuru a ohyb světla. Nazývají se klasické ne ve spojitosti s klasickou fyzikou, ale spíše proto, že jsou tyto experimenty dnes již „klasikou“, mají své pevné místo v historii fyziky i v začátcích studia relativity. Nemohly tak chybět ani v tomto textu. Nepatří ale čistě do historie, protože jak jsme se zmínili, jsou neustále opakovány a zpřesňovány. Práce experimentálních fyziků není nikdy u konce, protože nikdy si neřekneme, že tohle už stačí, že už víme dost.
Viděli jsme i některé modernější experimenty, Hafeleův-Keatingův, Gravity Probe B a jiné. A je ještě celá řada experimentů a jevů spojených s obecnou relativitou, které jsme nezmínili. Naším cílem zde není ani tak podat vyčerpávající seznam experimentů, ale ukázat, že na té obecné relativitě něco bude, protože ty zvláštní věci, které předpovídá, se opravdu dějí. A není zvláštnější předpovědi OTR, než jsou černé díry.
Černé díry
Jen málokdo dnes už alespoň neslyšel o černých dírách. Jde pravděpodobně o nejpopulárnější předpověď obecné relativity. Stručně řečeno se jedná o objekt s natolik silnou gravitací, že z něj nemůže uniknout ani světlo. Je mimochodem zajímavé, že první úvahy o podobných objektech pochází již z 18. století a jsou tedy založeny na klasické teorii gravitace. Ve středoškolských učebnicích můžeme najít vztah pro tzv. únikovou rychlost \(v_ú\), kterou bychom museli být vystřeleni kolmo vzhůru z povrchu kulové planety (neuvažujeme-li její rotaci) o poloměru \(R\) a hmotnosti \(M\), abychom unikli z jejího gravitačního působení a nebyli vtaženi zpět. Dá se spočítat jednoduše jako \(v_ú=\sqrt{2GM⁄R}\). Například po dosazení parametrů Země dostáváme pro únik z rovníku rychlost zhruba \(11{,}2\:\text{km/s}\). Tato hodnota se nazývá 2. kosmická rychlost. Pokud bychom hmotnost dané planety považovali za konstantní a jenom zmenšovali její poloměr, tj. planeta by se stávala stále kompaktnější, vidíme, že poroste i příslušná úniková rychlost. Nabízí se tedy otázka, jak daleko může tato úniková rychlost růst. Již v 18. století byla největší známou rychlostí rychlost světla, takže se (minimálně z dnešního hlediska) zdá být rozumné alespoň hypoteticky uvažovat o objektu, jehož úniková rychlost by byla rovna rychlosti světla nebo ji dokonce přesahovala (samozřejmě také ale vyvstává otázka, zda by světlo bylo gravitací takového objektu skutečně ovlivněno – to je debata, které jsme se věnovali v předchozí podkapitole). Pokud do vztahu pro únikovou rychlost jednoduše dosadíme \(v_ú=c\), můžeme snadno vyjádřit, že pro poloměr takového tělesa platí \begin{equation*} c=\sqrt{\frac{2GM}{R}}\implies R=\frac{2GM}{c^2}\equiv r_\text{S}. \end{equation*} To je ale přesně výraz, který se objevuje ve Schwarzschildově metrice \eqref{4.22} a který jsme označili jako Schwarzschildův poloměr. Není třeba zde hledat nějakou hlubší souvislost. Že nám klasická teorie gravitace dává podobný výsledek jako OTR je v tomto případě spíše náhoda (i když samozřejmě jistá spojitost tu je, například oba vzorce vycházejí za předpokladu sféricky symetrického centrálního tělesa). V každém případě vidíme, že jisté opatrné úvahy o hypotetických „černých hvězdách“, tedy hvězdách tak kompaktních, že by z nich nemohlo uniknout ani světlo, existovaly už dlouho před příchodem moderní relativity. Pro nás je to předznamenání toho, že diskuze o černých dírách bude z velké části diskuzí o tom, co se děje na Schwarzschildově poloměru.
V této podkapitole bude ještě více než jinde v tomto textu platit, že nám budou muset některé vzorce „spadnout z nebe“. Budeme se totiž snažit ilustrovat předpokládané vlastnosti černých děr tak, že necháme padat nejdříve světlo a pak i hmotné těleso na hypotetický objekt, který je menší než jeho příslušný Schwarzschildův poloměr. K tomu je ale zapotřebí matematicky řešit rovnici geodetiky, protože, jak už víme, volně padající objekt či světlo se v zakřiveném prostoročasu pohybují po svých příslušných geodetikách. To už je ale opravdu nad naše momentální matematické možnosti, protože jak odvození, tak některé výsledky jsou zde již opravdu matematicky komplikované. V některých případech bude dokonce názornější, než abychom zkoumali vlastnosti složitého vzorce, pomoci si obrázkem. Odvození všech zmíněných vztahů je samozřejmě možné najít ve vysokoškolských relativistických učebnicích jako např. [xi] nebo [xii].
Pojďme na začátek využít vzorec pro \(r_\text{S}\) k rychlému odhadu. Jakou zhruba hustotu by mohlo mít těleso, které má velikost svého Schwarzschildova poloměru? Když vyjdeme z definice hustoty jako hmotnosti vydělené objemem, pro objem tělesa použijeme známý vzorec pro objem koule a dosadíme za Schwarzschildův poloměr, dostáváme \begin{equation*}\label{4.33}\tag{4.33} \rho=\frac{M}{V}=\frac{M}{\frac{4}{3}\pi r_\text{S}^3}=\frac{M}{\frac{4}{3}\pi \left(\frac{2GM}{c^2}\right)^3}=\frac{3Mc^6 }{32\pi G^3M^3}=\frac{3c^6}{32\pi G^3M^2}. \end{equation*} Tímto vztahem dostáváme odhad na průměrnou hustotu tělesa. Vidíme, že je závislý na hmotnosti tělesa a zároveň s rostoucí hmotností průměrná hustota klesá. Pokud bychom například do vztahu dosadili hmotnost Slunce jako \(1{,}989\cdot10^{30}\:\text{kg}\), dostáváme hustotu přibližně \(1{,}85\cdot10^{19}\:\text{kg/m}^3\). To je na hustotu opravdu velké číslo (pro srovnání hustota železa je „pouhých“ \(7800\:\text{kg/m}^3\)). Tato hodnota je řádově srovnatelná s hustotou atomových jader (průměrná se uvádí jako přibližně \(2{,}3\cdot10^{17}\:\text{kg/m}^3\)). Je samozřejmě pravděpodobné, že zde používáme klasické vzorce, které ve skutečnosti v této situaci moc dobře nefungují (přece jen už víme, že silná gravitace odpovídá silnému zakřivení prostoročasu a v tom případě už samotný vzorec pro objem koule ztrácí smysl), a zároveň se ještě budeme zmiňovat o komplikacích s určením skutečného rozměru černé díry. Nicméně poselství našeho klasického odhadu je jisté. Pokud existuje objekt, jehož rozměr je srovnatelný či menší než příslušný Schwarzschildův poloměr, bude jeho hustota extrémní.
Poznámka 4.14
K diskuzi o černých dírách se hodí udělat si malou rychlou exkurzi do astrofyziky a konečných fází života hvězd. Dnes už víme, že hvězdy jsou tvořeny plazmatem, tj. natolik žhavým plynem, že dochází k vytržení některých elektronů z atomů (tzv. ionizaci) a plyn se stává směsí vytržených volných elektronů, zbylých kladných iontů a případně dosud neionizovaných neutrálních atomů. Každá hvězda se pravděpodobně zrodila z mračna vesmírného prachu, který se působením gravitace začal v jednom místě shlukovat, čímž se tam začala zvyšovat hustota, teplota a tlak. Při dostatečném zvýšení teploty a tlaku se zažehne termojaderná reakce, kdy se jádra lehkých prvků slučují na těžší jádra (nejčastěji vodík na helium), a uvolňuje se velké množství energie (celý tento proces je zajímavá kapitola sama pro sebe, ale pro naše povídání nyní není podstatný, zvídavý čtenář si o něm jistě něco může přečíst sám). Díky uvolněné energii má hvězda tendenci se rozpínat, čímž se vykompenzuje její gravitační kolaps. Po většinu svého života tak hvězda existuje díky této rovnováze mezi smršťováním a rozpínáním. Když už hvězda nemůže dále provádět jadernou syntézu (a zde opravdu vynecháváme spoustu zajímavých detailů), její hlavní životní fáze končí a typicky nastane jedna ze tří následujících možností v závislosti na hvězdné hmotnosti.
Nejméně hmotné hvězdy skončí jako bílí trpaslíci. Díky své relativně malé hmotnosti nemohou vytvořit dostatečné podmínky pro syntézu těžších prvků než je uhlík a kyslík. Jakmile dojde k zastavení termojaderné reakce, hvězda odhodí vrchní slupky a zbyde pouze pomalu vyhasínající jádro tvořené typicky právě uhlíkem a kyslíkem. Toto jádro je typicky velmi husté. Zatímco má hmotnost srovnatelnou se Sluncem, typické rozměry bílých trpaslíků jsou spíše jako naše planeta. Řádově tak mluvíme o hustotě okolo \(10^9\:\text{kg/m}^3\), milionkrát hustší než voda (jedná se samozřejmě, stejně jako dále, jen o jakousi průměrnou hodnotu, je nepravděpodobné, že by hvězda měla všude stejnou hustotu, směrem do jejího středu by se hustota měla zvyšovat). V bílém trpaslíku již nedochází k syntéze prvků, dalšímu gravitačnímu stlačování se brání díky tlaku tzv. degenerovaného elektronového plynu. Stručně řečeno, jedná se o kvantově-mechanický jev odpuzování mezi elektrony, které nechtějí (podle Pauliho vylučovacího principu) sdílet stejný kvantový stav (tedy mimo jiné být na jednom místě). Nemáme tím na mysli elektrické odpuzování.
Již jsme se zmínili o neutronových hvězdách. To je druhá možnost závěrečné fáze hvězdy. U hmotnějších hvězd (odhaduje se na \(10\) až \(25\) hmotností Slunce) je gravitační kolaps na konci života tak silný, že dojde k překonání zmíněného tlaku degenerovaného elektronového plynu ve zbylém jádru. Někdy se v populární literatuře můžeme dočíst o zatlačení elektronů do protonů za vzniku neutronů, ale poněkud přesnější formulace je, že za extrémních podmínek při vzniku neutronové hvězdy dochází k jaderným reakcím, kdy z protonů a elektronů (a dalších částic) vzniknou neutrony. Nyní je gravitační kolaps opět vykompenzován, protože mezi neutrony existuje rovněž odpuzování (nikoli ale elektrické, neutrony jsou elektricky neutrální, jedná se opět o kvantově-mechanický efekt). Hustota těchto objektů vychází řádově kolem \(10^{17}\:\text{kg/m}^3\), tedy právě zhruba jako hustota atomových jader. Díky vyšší hmotnosti původní hvězdy je také odhození vnějších obálek extrémnější než u bílých trpaslíků. Jedná se doslova o výbuch, kterému říkáme supernova. Neutronové hvězdy jsou pro astrofyziky velmi zajímavé nejen díky jejich silnému gravitačnímu poli, jak jsme se již zmínili, ale také díky jejich typicky velmi silnému magnetickému poli.
Zatímco bílí trpaslíci mají poloměr řádově tisíckrát větší než je jejich příslušný Schwarzschildův poloměr, u neutronových hvězd je tento poměr již řádu jednotek. Co když je ale hmotnost hvězdy natolik velká, že i po výbuchu a odhození vnějších vrstev bude hmotnost zbylého jádra příliš velká a odpuzování neutronů nedokáže gravitační kolaps zastavit? Hustota poroste, zbylé jádro hvězdy se bude smršťovat, až nakonec zkolabuje do něčeho menšího, než je jeho Schwarzschildův poloměr. Vznikne černá díra, objekt, který byl po velkou část \(20.\) století pouze podivnou teoretickou předpovědí.
Shrňme si nyní, co už na téma černých děr víme z hlediska relativity. První náznak přišel už se Schwarzschildovou metrikou \eqref{4.22}. Ta v sobě obsahuje výraz \(1-2GM/c^2r\) ve dvou metrických koeficientech, z toho u jednoho ve jmenovateli. Čistě z matematického hlediska je tedy zřejmé, že rovná-li se radiální souřadnice Schwarzschildovu poloměru, tj. \(2GM/c^2\), nastává problém. Podobný problém nastává i pro \(r=0\). Hovoříme o tzv. singularitách, ale jak si za chvilku ukážeme, nejedná se o singularity stejného typu. U ohybu světla jsme také viděli, že světelný paprsek, který vstoupil do oblasti dané \(r_\text{S}\), z ní již nevystoupil. Hranici vytyčené Schwarzschildovým poloměrem se proto také říká horizont událostí, protože za něj, stejně jako u běžného zemského horizontu, „nevidíme“ – ani světlo a tím pádem ani žádná jiná informace se nám nevrátí zpět (a událostí proto, že ohraničuje nejen část prostoru, ale prostoročasu, který je, jak už víme, tvořen událostmi podobně jako prostor je tvořen body).
Ukažme si nyní, co vše nám Schwarzschildova metrika dokáže říci o těchto singularitách. Prozatím tedy předpokládejme, že existuje tak husté těleso, že je menší než jeho Schwarzschildův poloměr. Tím pádem je prakticky možné se na tuto hodnotu souřadnice dostat. Začněme tím, že směrem k tělesu vyšleme radiálním směrem světelný paprsek. Když jsme se ve třetí části bavili o prostoročasovém intervalu, ukázali jsme, že pro světlo je interval vždy nulový. To zůstává pravda i v obecné relativitě. Zároveň díky čistě radiálnímu směru pro paprsek platí \(\text{d}\varphi=0\). Metrika se tedy zjednoduší na \begin{equation*} (\text{d}s)^2=-\left(1-\frac{r_\text{S}}{r}\right)c^2(\text{d}t)^2+\frac{(\text{d}r)^2}{1-\frac{r_\text{S}}{r}}=0. \end{equation*} Nyní můžeme vyjádřit poměr dr/dt, což odpovídá změně radiální souřadnice podle souřadnicového času, takže tzv. souřadnicové rychlosti: \begin{equation*}\tag{4.34}\label{4.34} \frac{(\text{d}r)^2}{(\text{d}t)^2} =\left(\frac{\text{d}r}{\text{d}t}\right)^2=c^2\left(1-\frac{r_\text{S}}{r}\right)^2\implies \frac{\text{d}r}{\text{d}t}=±c\left(1-\frac{r_\text{S}}{r}\right). \end{equation*} Znaménko plus odpovídá paprsku letícímu směrem od středu, nás tedy zajímá řešení s mínusem. Dostali jsme zvláštní výsledek, že souřadnicová rychlost světla není rovna vždy \(c\), ale pro jakoukoli konečnou souřadnici \(r\) je menší. To se zdá být v rozporu se speciální relativitou, ale ta mluví o neměnnosti rychlosti světla pouze v inerciálních soustavách a ty můžeme v gravitačním poli realizovat pouze lokálně pomocí volného pádu. Připomeňme, že souřadnicový čas má fyzikální význam vlastního času pozorovatele v nekonečnu (hodně daleko mimo efektivní dosah gravitačního pole), podle našeho výsledku se tedy bude pro vzdáleného pozorovatele světelný signál v gravitačním poli zpomalovat. Tomuto jevu se říká Shapirův efekt. Byl předpovězen americkým astrofyzikem Irwinem Shapirem v roce 1964 o několik let později i experimentálně potvrzen pomocí radarových signálů, které byly vyslány ze Země a odraženy od Venuše a Merkuru. Signály byly vyslány ve dvou různých situacích. Nejprve aby na své cestě ke každé z planet prošly v těsné blízkosti Slunce, tj. co nejsilnějším gravitačním polem. Čas, za který se signál vrátil, byl poté porovnán s časem návratu signálu vyslaného tehdy, kdy na cestě k planetám a zpět prošel ve větší vzdálenosti od Slunce (ve skutečnosti bylo vyslaných a porovnávaných signálů v experimentu mnoho, ale princip je v zásadě podobný). Obecná relativita předpovídá, že elektromagnetický signál bude v tomto experimentu zpožděn řádově o stovky mikrosekund, což je přesnost, se kterou bylo v 70. letech minulého století již možné pracovat. Výsledek experimentu (a i dalších později zopakovaných) byl pochopitelně v souladu s teorií a dnes je Shapirův efekt často označován jako čtvrtý klasický experiment obecné relativity.
Nenechme se ale zmást. Shapirův jev není způsoben skutečným zpomalením světla v gravitačním poli. Je přímým důsledkem gravitační dilatace času a deformace prostoru. Už víme, že vzdálenému pozorovateli plyne čas rychleji, než blíže k centrálnímu tělesu, a zatímco souřadnice \(r\) je pro vzdáleného pozorovatele tam u něj prakticky totéž co radiální vzdálenost, v silnějším gravitačním poli to neplatí. Představme si, že stojíme na nějaké konkrétní hodnotě radiální souřadnice a radiálně vyslaný světelný signál proletí kolem nás. Jakou rychlost mu naměříme? Stačí si vzpomenout na vztahy \eqref{4.24} a \eqref{4.25}, podle kterých pro malé přírůstky našeho vlastního času \(\tau\) a reálně naměřené radiální vzdálenosti \(l\) platí \(\text{d}\tau=\text{d}t\sqrt{1-\frac{r_\text{S}}{r}}\) a \(\text{d}l=\frac{\text{d}r}{\sqrt{1-\frac{r_\text{S}}{r}}}\). Námi změřená rychlost paprsku tedy bude \begin{equation*} \frac{\text{d}l}{\text{d}\tau}=\frac{\frac{\text{d}r}{\sqrt{1-r_\text{S}/r}}}{\text{d}t\sqrt{1-r_\text{S}/r}}=\frac{1}{\left(1-\frac{r_\text{S}}{r}\right)}\frac{\text{d}r}{\text{d}t}=-\frac{1}{\left(1-\frac{r_\text{S}}{r}\right)}\left(1-\frac{r_\text{S}}{r}\right)c=-c. \end{equation*} V libovolném místě gravitačního pole tedy naměříme skutečně rychlost světla rovnou \(c\), jak bychom čekali.
Vraťme se nyní ke vztahu \eqref{4.34}. Pokud do něj dosadíme \(r=r_\text{S}\), dostáváme nulu. Pro vzdáleného pozorovatele by se tedy měl světelný paprsek na Schwarzschildově poloměru zdánlivě zastavit. To se jistě zdá zvláštní. Navíc i proto, že v numerické simulaci chodu paprsku v předcházející kapitole jsme viděli, jak paprsek horizontem událostí projít může. Čím je tento rozpor způsoben? Než na tuto otázku odpovíme, podívejme se ještě, jak se při pádu do černé díry chová hmotné těleso.
Začněme opět něčím, co nám bude povědomé. Když bychom chtěli v gravitačním poli stát na nějaké vzdálenosti \(r\) od středu gravitujícího tělesa, podle Newtonova gravitačního zákonu musíme soustavně překonávat gravitační sílu (například tryskami rakety), jejíž velikost je rovna \(GmM/r^2\) , kde \(m\) je naše hmotnost. Pro Schwarzschildův prostoročas lze odvodit podobně velikost síly, kterou musí naše motory působit, aby nás udržely v klidu na konstantní souřadnici \(r\) jako \begin{equation*}\label{4.35}\tag{4.35} F=\frac{GmM}{r^2\sqrt{1-\frac{r_\text{S}}{r}}}. \end{equation*}
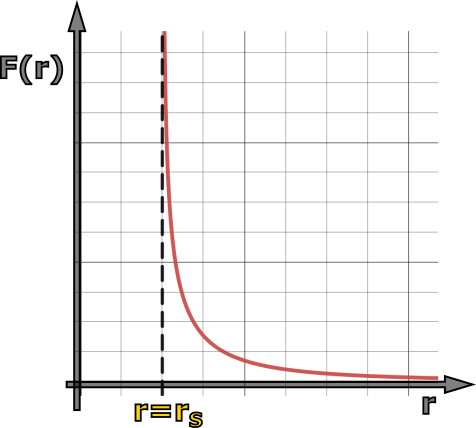
Obrázek 4.51 Vykreslení funkce \eqref{4.35}. V grafu neuvádíme konkrétní číselné hodnoty, protože ty závisí na volbě \(m\) a \(M\) a nejsou pro nás důležité.
Vidíme, že pro libovolnou hodnotu souřadnice \(r\) větší než \(r_\text{S}\) dostáváme větší velikost síly než klasickým vzorcem (protože ve vztahu \eqref{4.35} vždy dělíme odmocninou, která je menší než \(1\)). Zároveň si také můžeme všimnout, že pro hodně velké \(r\), je člen \(r_\text{S}/r\) oproti jedničce zanedbatelný a dostáváme klasický vztah, pro slabé gravitační pole si tedy relativistický a klasický vztah odpovídají. Opět nám zde nefunguje přímé dosazení \(r=r_\text{S}\), ale můžeme se na vztah podívat jako na matematickou funkci \(F(r)\), vykreslit si příslušný graf a podívat se na její chování, když se blížíme k horizontu událostí (obrázek 4.51). Vidíme, že s přibližováním se na horizont událostí roste potřebná síla nade všechny meze. Pro \(r=r_\text{S}\) je tedy, stručně řečeno, nekonečná. Prakticky tedy docházíme k výsledku, že na horizontu již není možné stát na místě. Co by se tedy s námi stalo, kdybychom dosáhli horizontu?
Pokud budeme například padat na černou díru z velké dálky, je možné pomocí již zmíněné rovnice geodetiky odvodit, jak se bude naše poloha (tj. radiální souřadnice) vyvíjet s časem. Kupodivu ale dostaneme velmi odlišné výsledky, pokud budeme sledovat naši polohu jako funkci souřadnicového času \(r(t)\), tedy tak, jak by to viděl vzdálený statický pozorovatel, nebo pokud ji budeme sledovat jako funkci našeho vlastního času \(r(\tau)\). Jak je tohle možné? Již jsme například viděli, že z metriky a jiných rovnic je možné vyjádřit vztahy typu \(\text{d}r/\text{d}t\) nebo \(\text{d}r/\text{d}\tau\) tedy radiální rychlost v souřadnicovém čase nebo ve vlastním čase tělesa. Z vývoje rychlosti je pak možné (v tomto případě nutně integrací, protože se nejedná o jednoduchý pohyb například s konstantním zrychlením) vypočítat, jak se mění radiální souřadnice podle daného času (tj. daného pozorovatele). Protože jsou tyto vztahy ale už trochu nepřehledné, pomozme si opět grafem (obrázek 4.52).
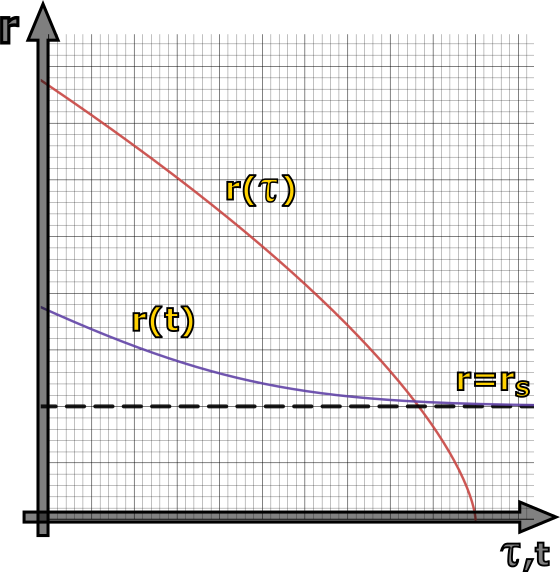
Obrázek 4.52 Graf časového vývoje radiální souřadnice tělesa padajícího na černou díru z nekonečna vzhledem k času pozorovatele v nekonečnu \(r(t)\) (tzv. souřadnicový čas) a vlastnímu času padajícího tělesa \(r(τ)\). Podle vzdáleného pozorovatele radiální souřadnice tělesa nikdy neklesne pod \(r_\text{S}\), těleso se na něm zastaví (fialová křivka). Ve skutečnosti ale těleso skrz horizont padá dovnitř černé díry, jak ukazuje jeho červená křivka. Graf je pouze ilustrační, číselné hodnoty závisí na konkrétní situaci (tj. hmotnosti černé díry).
Zaměřme se nejprve na to, jak pád tělesa vidí vzdálený pozorovatel, tedy \(r(t)\). V grafu na fialové křivce vidíme, jak se radiální souřadnice tělesa blíží k Schwarzschildovu poloměru, ale nikdy jej nepřekročí. Těleso se zdá zastavit na horizontu událostí a dál nepokračuje. To je rozhodně zvláštní předpověď. Proč by se mělo těleso zastavit? A znamená to, že při kolapsu velmi hmotné hvězdy se většina její hmoty prostě zastaví na souřadnici \(r_\text{S}\)? A co ta hmota, která je ve hvězdě na nižší radiální souřadnici už od začátku? Potřebujeme ještě další vodítko, a tím je právě závislost \(r(\tau)\). Kdo jiný by měl rozhodnout o osudu padajícího tělesa než těleso samotné? V grafu máme červeně vykreslený tento průběh radiální souřadnice tělesa v závislosti na jeho vlastním čase, tedy tak, jak to „vidí“ těleso samo (stejně tak bychom mohli mluvit o pozorovateli padajícím na černou díru, ale nechceme si zbytečně komplikovat situaci dalším rozlišováním dvou pozorovatelů). Z grafu je jasně vidět, že těleso prochází horizontem událostí a v konečném čase padá dále až na \(r=0\).
Proč je tedy předpověď vzdáleného pozorovatele natolik odlišná? Odpověď nám může poskytnout gravitační rudý posuv. Vžijme se do role vzdáleného pozorovatele a sledujme libovolné těleso (například námi vyslanou sondu) padat na černou díru. Skutečnost, že sondu pozorujeme, znamená, že k nám vysílá nějaký elektromagnetický signál (například ji zcela obyčejně vidíme, protože k nám od ní přichází světlo). Jak se ale sonda přibližuje k horizontu událostí, snižuje se frekvence signálu, který k nám přichází, jak signál „šplhá“ ven z gravitačního pole. Tato změna naměřené frekvence je dána odlišným plynutím času v různých místech gravitačního pole. Čím je sonda „hlouběji“ v gravitačním poli, tím jí oproti nám plyne čas pomaleji. V rovnici \eqref{4.24} jsme odvodili vztah mezi vlastním časem \(\text{d}\tau\) tělesa stojícího na radiální souřadnici \(r\) a časem vzdáleného pozorovatele \(\text{d}t\). Pro případ sondy volně padající z velké dálky je možné odvodit podobný vztah: \begin{equation*}\label{4.36}\tag{4.36} \text{d}\tau=\text{d}t\left(1-\frac{r_\text{S}}{r}\right). \end{equation*}
Rovnice \eqref{4.36} se liší od statické situace \eqref{4.24} tím, že místo odmocniny máme přímo závorku na první mocninu. To můžeme pochopit tak, že kromě gravitačního efektu dilatace času je zde také již naše stará známá kinematická dilatace času (protože sonda se od nás vzdaluje měnící se rychlostí \(v\)). Můžeme si to tedy představit tak, že se ve vztahu objevují odmocniny dvě: \(\sqrt{1-\frac{r_\text{S}}{r}}\sqrt{1-\frac{v^2}{c^2}}\), kde ta druhá pochází z gama faktoru. Ukazuje se, že rychlost volně padajícího tělesa z nekonečna na dané radiální souřadnici dopadne ve Schwarzschildově prostoročasu stejně jako v klasické mechanice: \(v=\sqrt{2GM/r}\) (tento vztah jsme již viděli jako únikovou rychlost z daného místa, to je proto, že celá situace je symetrická. Minimální rychlost, kterou potřebuji, abych z daného místa gravitačního pole radiálně unikl do nekonečna, je stejná jako rychlost, kterou bych nabral cestou zpět volným pádem z nekonečna.). Když dosadíme za \(v\) do odmocniny, dostáváme hledaný výsledek.
Nyní můžeme vyjádřit frekvenci, kterou zachytíme v nekonečnu \(f_\infty\) pomocí frekvence, kterou vysílá sonda \(f_1\) (tu považujeme za stálou). Stačí si uvědomit, že zachycená frekvence je převrácená perioda daného vlnění, a naměřená perioda je úměrná plynutí našeho času. Zjednodušeně tedy můžeme psát \begin{equation*}\label{4.37}\tag{4.37} \frac{f_\infty}{f_1}=\frac{\frac{1}{\text{d}t}}{\frac{1}{\text{d}\tau}}=\frac{\text{d}\tau}{\text{d}t}=\left(1-\frac{r_\text{S}}{r}\right)=\implies f_\infty=f_1\left(1-\frac{r_\text{S}}{r}\right). \end{equation*}
Naším výsledkem tedy je, že jak se sonda blíží k \(r_\text{S}\), klesá námi zachycená frekvence až na nulu. Jinými slovy, přestáváme zachycovat vysílaný signál. Zároveň, když si vzpomeneme na vztah \eqref{4.34}, rychlost světla a tím pádem i signálu ze sondy z našeho pohledu také klesá k nule, jak se sonda blíží k horizontu. To znamená, že čas, než k nám tento signál doputuje, je čím dám tím větší. Limitně řečeno, až sonda dojde na horizont, případný signál nám putuje nekonečně dlouho, neboli nikdy k nám nedorazí. Poslední co vidíme, je obraz sondy těsně před tím, než se dostala k horizontu, ale z našeho pohledu ho nepřekročí. Nepřijde k nám o tom žádná informace. To tedy vysvětluje zdánlivý rozpor vyjádřený grafem (4.52).
Poznámka 4.15
Obrázek 4.53 Náčrtek k výpočtu relativního rozdílu zrychlení, které v gravitačním poli působí na naše nohy a hlavu.
V dosavadních a i následujících úvahách předpokládáme, že sonda svůj pád přežívá bez úhony. Ve skutečnosti se klidně může stát, že bude sonda ještě před dosažením horizontu roztrhána gravitačními slapovými silami. Tento výraz je často spojován s přílivem a odlivem, které jsou způsobeny různým gravitačním působením Měsíce a Slunce v různých místech naší planety. A i když již v relativitě nemluvíme o gravitační síle, výraz slapové síly se stále používá čistě z praktických důvodů. Striktně vzato, pokud právě neležíte, tak na vaše nohy a hlavu působí jinak silná gravitace. Rozdíl těchto působení je samozřejmě tak malý, že ho prakticky nijak nepocítíte a v případě Země se projevuje až na velkých vzdálenostech. Kdybychom se ale přiblížili dostatečně blízko k černé díře, míra narůstání gravitačního působení se může zvýšit natolik, že naše nohy (pokud bychom padali nohama napřed) budou urychlovány výrazně více než naše hlava, což by nás mohlo doslova roztrhat.
Můžeme si to ilustrovat pomocí klasického gravitačního zákona. Představme si, že stojíme na povrchu Země. Našim nohám tedy gravitace uděluje zrychlení \(a_1=GM/R_Z^2\). Označíme-li naši výšku \(h\), pak na naši hlavu působí gravitační zrychlení přibližně \(a_2=GM/(R_Z+h)^2\). Spočítejme nyní relativní rozdíl těchto dvou zrychlení vztažený k \(a_1\). Relativní proto, že nás nutně nezajímá, o kolik přesně se liší, ale jak moc se liší: \begin{equation*} \frac{a_1-a_2}{a_1}=1-\frac{a_2}{a_1}=1-\frac{\frac{GM}{(R_Z+h)^2}}{\frac{GM}{R_Z^2}}=1-\frac{R_Z^2}{(R_Z+h)^2}=\frac{(R_Z+h)^2-R_Z^2}{(R_Z+h)^2}=\frac{2R_Zh+h^2}{(R_Z+h)^2}. \end{equation*} Je zajímavé, že výsledek nezávisí na hmotnosti planety, ale pouze na jejím poloměru a zvolené výšce \(h\). Aniž bychom museli počítat konkrétní čísla, vidíme, že pokud bychom směstnali hmotu Země do polovičního objemu, ale sami přitom zůstali na původním místě, relativní rozdíl zrychlení a dokonce ani zrychlení samotná se nezmění. To je dáno tím, že gravitační pole sféricky symetrického těleso závisí pouze na jeho hmotnosti a naší vzdálenosti od jeho středu, nikoli na rozměrech tělesa samotného. Na povrchu Země tedy působí stejné slapové síly jako v okolí černé díry hmotnosti Země, pokud zůstaneme \(6378\:\text{km}\) daleko. V případě černé díry je ale na rozdíl od Země možné se dostat na výrazně menší radiální souřadnici (ve vztahu výše můžeme \(R_Z\) vyměnit za obecné \(r\)), a tím zažít větší slapové síly. Nemusíme se nutně bavit o mezích pevnosti lidského těla, určitě ale nějaké existují a pádem na černou díru mohou být dříve či později překročeny. Navíc kromě zmíněného natahování v radiálním směru dochází i ke stlačování v tečném směru (je to stejná (ale extrémnější) situace jakou jsme viděli u přibližování se dvou dostatečně dlouho volně padajících kamenů např. na obrázku 4.20).
Paradoxně máme větší šanci projít horizontem událostí velmi hmotných a tím pádem velkých černých děr, kde slapové efekty nejsou tak silné. To se zdá být zvláštní. Ale dá se to pochopit na příkladu slapových sil na povrchu Země a Slunce. Gravitační zrychlení na povrchu Slunce je asi \(28\)krát větší než na povrchu Země, přesto je relativní rozdíl mezi zrychleními způsobenými naší hlavě a nohám menší, protože ve vztahu výše nehraje hmotnost gravitujícího tělesa roli a na povrchu Slunce jsme určitě na větší radiální souřadnici. Stejně tak u masivních černých děr je Schwarzschildův poloměr velký a máme větší šanci překročit horizont dříve, než nás slapové působení roztrhá.
Ze všeho, co jsme zatím řekli, zejména z faktu, že (slapové síly stranou) sonda bez problému projde horizontem, plyne, že singularita \(r=r_\text{S}\) ve Schwarzschildově metrice není fyzikálního charakteru. Nejedná se o oblast s nekonečnou křivostí nebo podobně zvláštním chováním, při průchodu horizontem byste neprožili žádnou zvláštní změnu, ani byste si nevšimli, že jste právě vstoupili do oblasti, ze které není návratu. Neunikne z ní světlo a neuniknete z ní ani vy. Přesto ale naše matematika ve Schwarzschildově metrice pro \(r=r_\text{S}\) selhává a měli bychom si vysvětlit proč. Jedná se totiž o tzv. souřadnicovou singularitu. Jedná se o bod či oblast, kde dané souřadnice selhávají ne z nějakého objektivního a realitou podloženého důvodu, ale čistě jako důsledek své definice. Například se s něčím takovým můžeme potkat na povrchu koule při použití sférických souřadnic. Vzpomeňme si, že na sféře jsme zavedli metriku pomocí úhlových souřadnic \(\theta\) a \(\varphi\) jako \((\text{d}s)^2=r^2(\text{d}\theta)^2+r^2\sin^2{\theta} (\text{d}\varphi)^2\). Pokud bychom ale chtěli například počítat vzdálenost mezi dvěma body vedoucí přes „severní pól“, pro nějž je \(\theta=0\), tak máme problém, protože druhý metrický koeficient je tam díky funkci sinus automaticky nulový. Zároveň jsou souřadnice severního pólu nejednoznačně určeny, protože není jasné, jakou souřadnici \(\varphi\) („zeměpisnou délku“) mu přiřadit. Tyto komplikace nevznikly proto, že by se zde geometrie sféry chovala nějak jinak než na zbytku plochy, je to čistě vlastnost použitých souřadnic, které dobře fungují všude jinde kromě pólů (na jižním pólu jsme v obdobné situaci). Pokud bychom chtěli pomocí metriky proměřovat vzdálenosti v okolí pólu, je třeba vybrat jiné souřadnice nebo aspoň tyto pootočit, aby byl „pól“ někde jinde. Podobné je to i u polárních souřadnic v rovině. Tam byla každému bodu přiřazena vzdálenost od počátku \(r\) a úhel \(\varphi\) vzhledem k vybrané ose, metrika pak byla \((\text{d}s)^2=(\text{d}r)^2+r^2(\text{d}\varphi)^2\). Zde nám dělá problém počátek souřadnic, jednak je pro něj \(r=0\) (čili opět problém s metrickým koeficientem v počátku) a podobně jako v předchozím není jasné, jakou hodnotu souřadnice \(\varphi\) mu přidělit. Kdekoli mimo počátek ale nemáme problém. U křivočarých souřadnic je toto chování mimochodem poměrně časté. Důsledkem jejich zavedení může být, že pro některé body či množiny bodů nefungují (tj. nedávají rozumné výsledky). Ve výsledku nám to ale nemusí vadit, stačí, když pracujeme jen s oblastí, kde fungují dobře.
Selhání Schwarzschildovy metriky na horizontu tedy není z fyzikálního důvodu, ale je dáno vlastnostmi použitých souřadnic. Při popisu souřadnic \(r\) a \(t\) jsme si ukazovali, že se dají dobře interpretovat vzhledem k pozorovateli stojícímu v nekonečnu (jeho vlastní čas a jím měřené vzdálenosti tam hodně daleko). Už jsme si ale rozmysleli, že právě tento pohled nefunguje v oblasti horizontu příliš dobře. Například čas padající sondy se na horizontu z pohledu vzdáleného pozorovatele podle \eqref{4.36} zastaví. Ne proto, že by se sondě doopravdy zastavil čas, ale zakřivení prostoročasu a zejména jeho efekt na světlo jsou zde natolik silné, že naše vnější měření přestává zcela odpovídat realitě. Singulární chování metriky na horizontu je toho matematickým důsledkem. Dodejme, že existuje mnoho jiných souřadnicových systémů používaných ve Schwarzschildově prostoročasu, které tento neduh nemají, na druhou stranu mohou být o poznání těžší na pochopení a nebudeme je zde potřebovat, takže se jimi nebudeme zabývat. Zájemci si mohou vyhledat např. Kruskalovy-Szerekesovy nebo Eddingtonovy-Finkelsteinovy souřadnice.
Možná vás napadá otázka, jak taková černá díra vypadá, ale v tom spočívá ta potíž. Jak to zjistit? Černá díra nevydává světlo, a i kdybychom do ní vypustili sondu, ta nám zpod horizontu nemá jak podat zprávu. Z toho důvodu je pro nás definujícím faktorem pro černou díru právě její Schwarzschildův poloměr (závisející na její hmotnosti). Černá díra je pro nás tedy prakticky víc oblastí ohraničenou jednocestnou „membránou“ než reálným objektem, který se skrývá pod ní a o kterém zatím nevíme prakticky nic. Libovolné těleso může překonat horizont událostí (i když už třeba ne v celku) a tím vstoupit do černé díry. Uvnitř horizontu již není možné ani stát na místě, a těleso tak nezadržitelně padá až do samého středu souřadnic, na druhý problematický bod \(r=0\). I ten způsobuje v metrice tohoto prostoročasu problém a tento problém sdílí i všechny ostatní možné používané souřadnice. Zdá se, že tady se děje něco zajímavějšího než je souřadnicová singularita.
Přestavme si kolabující jádro dostatečně hmotné hvězdy, jak je gravitací veškerá hmota stlačována do čím dál menšího prostoru, a to natolik silně, že ani vzájemné odpuzování částic nestačí na zastavení kolapsu. Průměrná hustota přerůstá i hustotu atomových jader a zakřivení okolního prostoročasu narůstá čím dál víc. V jednu chvíli je veškerá hmota stlačena pod příslušný Schwarzschildův poloměr, a tím je okolní prostoročas natolik zakřiven, že nemůže uniknout ani světlo. Z našeho pohledu z vnějšku vznikla černá díra. Co se ale děje uvnitř? Podle předpovědi obecné relativity, všechna hmota dále padá až na \(r=0\), není nic, co by ji zastavilo. To by ale znamenalo, že vzniká objekt s nulovým objemem a tedy nekonečně velkou hustotou. Bez důkazu také uveďme, že na \(r=0\) vychází i nekonečně velká prostoročasová křivost a nekonečně velké slapové síly. Narážíme na opravdovou fyzikální singularitu, bod, kde samotné fyzikální předpovědi přestávají dávat smysl. Prakticky v každé fyzikální teorii jsou nekonečna, která nedokážeme odstranit vhodnou změnou souřadnic, nahlížena jako nežádoucí a často bývají argumentem pro nedokonalost dané teorie. Konec konců, nekonečno je užitečný matematický nástroj, ale může být ve skutečnosti něco doopravdy nekonečné? Z toho důvodu si myslíme, že předpověď fyzikální singularity uvnitř černých děr poukazuje na limity obecné teorie relativity. Po celou dobu našeho textu představujeme OTR jako nástupce klasické teorie gravitace, složitější, ale přesnější teorii lépe vypovídající o povaze světa. Nikde jsme ale netvrdili, že je OTR finální teorií (což si ostatně nemůže nárokovat žádná současná vědecká teorie a je otázkou – v zásadě filozofickou – zda tomu tak někdy v budoucnu může být).
Dvě velké fyzikální teorie dvacátého století jsou obecná relativita a kvantová mechanika. Jedna se zabývá zejména gravitací, tedy typicky fyzikou velkých těles, druhá popisuje svět na té nejmenší úrovni. A jejich přístupy, matematický popis a aplikace jsou tím pádem výrazně odlišné. Natolik, že si tyto dvě teorie odporují již v některých základních předpokladech. Přesto, anebo možná právě proto, se je snaží fyzikové již několik desetiletí spojit dohromady či spíše zastřešit nějakou sjednocující teorií (tzv. teorie kvantové gravitace). Proč by taky měla být fyzika velmi malého zásadně odlišná od fyziky velmi velkého? Nebylo by krásné mít jednu ucelenou fyzikální teorii, která by sice pro různé situace dávala různé předpovědi, ale byla založena na jednotné sadě principů a fyzikálních zákonů? Minimálně pro fyziky to krásná představa je. Přesto ale na sjednocení teorie gravitace a kvantové mechaniky čekáme již desítky let. Proč o tom ale mluvíme? Vcelku rozumnou odpovědí na problém fyzikální singularity uvnitř černých děr je právě to, že díky obrovskému stlačení hmoty do mikroskopických rozměrů se zde chtě nechtě pohybujeme už na pomezí nebo zcela v říši kvantové fyziky. Je pravděpodobné, že se při takových hustotách látky uplatňuje nějaký dosud neobjevený kvantový efekt, který OTR neobsahuje a tím pádem v této situaci nedává rozumné výsledky. Jako většina fyzikálních teorií má její platnost své hranice a toto je jedna z nich.
Abychom to ilustrovali, můžeme zavzpomínat například na stavovou rovnici ideálního plynu, kterou potkáme na střední škole. Ta svazuje dohromady veličiny popisující stav plynu jako je tlak \(p\), objem \(V\), termodynamická teplota \(T\) a počet částic \(N\) pomocí rovnice \(pV=Nk_BT\), kde \(k_B\) je pro nás v tuto chvíli nedůležitá experimentální konstanta. Všimněme si, že pokud bychom podle této rovnice udržovali plyn na konstantním tlaku a snižovali jeho teplotu do nuly, dostáváme nulový objem, tedy opět nekonečně velkou hustotu. My samozřejmě dobře víme, že něco takového není reálně možné, už třeba proto, že při snižování teploty plyn dříve či později zkapalní, případně dále ještě ztuhne na pevnou látku a objeví se nové efekty, které smršťování zabrání. Stavová rovnice ideálního plynu tedy není obecně platnou, ale přesto jí s úspěchem používáme pro různé plyny, akorát to musí být pro takové teploty a tlaky, kdy to dává smysl (například okolo atmosférického tlaku a pokojové teploty). Jsme si vědomi mezí platnosti dané teorie a je třeba je respektovat.
Umíme tedy docela dobře popsat gravitační působení vně černých děr, a to nejen sféricky symetrických a nerotujících, kterým se věnujeme zde, ale jak už bylo řečeno, i složitějších rotujících či elektricky nabitých (příslušné prostoročasy jsou už pro nás z matematického hlediska opravdu příliš komplikované). OTR nám ale nedokáže odpovědět na otázku, jak vypadá černá díra uvnitř. K tomu by bylo zapotřebí teorie kvantové gravitace. Ta by také pravděpodobně výrazně přispěla k lepší představě o vzniku našeho vesmíru ve Velkém třesku, protože pustíme-li si současné rozpínání vesmíru pomyslně pozpátku, dojdeme nakonec také k singularitě, kdy je veškerá hmota vesmíru směstnána do jednoho bodu o nekonečně velké hustotě a teplotě. Současné fyzikální poznání nás sice dokáže dostat velmi blízko ke vzniku světa, ale ne až do pomyslného času \(t=0\:\text{s}\). Mimochodem, snaha o prozkoumání, co se skrývá pod horizontem černé díry, a následné vytvoření této sjednocující teorie je jedním z hlavních prvků zápletky vědecko-fantastického filmu Interstellar, na jehož vzniku spolupracoval také tým relativistů vedený Kipem Thornem (mimo jiné laureátem Nobelovy ceny za fyziku v roce 2017 za přispění k detekci gravitačních vln).
Nyní se dostáváme k té nejdůležitější otázce. Jsou černé díry čistě teoretickou předpovědí, nebo opravdu existují? Na to se samozřejmě dá odpovědět jen reálným pozorováním a v tom se skrývá první zdánlivý zádrhel. Jak pozorovat vesmírný objekt, který nezáří ve světelném ani jiném oboru elektromagnetického spektra? Naštěstí existuje způsob. I když samotnou černou díru vidět nemůžeme, můžeme pozorovat její gravitační interakci s něčím jiným, co už vidět dokážeme. Jedním z příkladů je \(16\) let trvající pozorování pohybu \(28\) hvězd nejbližších k centru naší galaxie. Z pozorování vyplývá, že hvězdy obíhají kolem společného gravitačního „středu“, ten ale ve světelném oboru nijak nezáří. Z orbit hvězd lze také odhadnout hmotnost tohoto neviděného tělesa – je hmotné jako čtyři miliony Sluncí! Na základě těchto pozorování se tedy zdá (jiný realistický astrofyzikální objekt by se do orbit těchto hvězd nevešel), že v jádru naší galaxie se nachází tzv. supermasivní černá díra, označovaná jako Sagittarius A* (na obloze se totiž nachází v souhvězdí Střelce) a je pravděpodobné, že tomu tak bude i v jádrech dalších galaxií.

Obrázek 4.54 Umělecké ztvárnění objektu Cygnus X-1. Zdroj: Evropská vesmírná agentura - https://www.esa.int/Science_Exploration/Space_Science/Observations_Seeing_in_X-ray_wavelengths .
Máme i další nepřímé náznaky existence černých děr. Jedním typem objektu pozorovaného astronomy jsou tzv. rentgenové dvojhvězdy. Dvojhvězdy, tedy systém dvou navzájem se obíhajících hvězd, se vyskytují poměrně hojně. Některé z nich ale vyzařují poměrně silně v rentgenovém oboru spektra. Protože naše atmosféra rentgenové záření (naštěstí pro nás) nepropustí, musí být pozorování v tomto oboru prováděna čistě pomocí satelitů na orbitě, a jedná se tak o poměrně mladé odvětví astronomie. Předpokládá se, že rentgenové záření vzniká, když jedna z hvězd (typicky se jedná o bílého trpaslíka či neutronovou hvězdu) gravitačním působením okrádá svou společnici o hvězdný materiál. Ten pak spirálovitě padá na „lupiče“ a vytváří tzv. akreční disk. Materiál se v disku silně zahřívá třením a tuto nahromaděnou energii vyzařuje zejména v rentgenovém spektru. U některých, zejména těch silněji vyzařujících, rentgenových dvojhvězd ale kompaktnější z objektů není vidět. Příkladem je objekt s názvem Cygnus X-1 v souhvězdí Labutě (latinsky Cygnus). Jako silný zdroj rentgenového záření je znám již od poloviny \(60.\) let minulého století, ale postupem času bylo ukázáno, že kompaktní složka dvojhvězdy je příliš malá na to, aby se jednalo o něco jiného než černou díru. Její hmotnost se odhaduje na přibližně \(21\) hmotností Slunce a je to historicky první vesmírný objekt obecně uznávaný jako černá díra. Mimochodem, i Sagittarius A* je zdrojem rentgenového záření, patrně díky svému akrečnímu disku.
Tím se dostáváme od nepřímých důkazů k přímým. Možná jste zachytili relativně nedávno zprávu o vyfocení černé díry. V roce 2019 byla uveřejněna fotografie supermasivní černé díry ve středu galaxie s označením M87, sama černá díra se podle toho označuje M87*. Její hmotnost je odhadována na \(6\) miliard (!) hmotností Slunce, je tedy asi \(1600\)krát větší než „náš“ Sagittarius A* a nachází se asi \(54\) miliónů světelných let od naší galaxie. Na získání jejího snímku spolupracovala celá řada observatoří po celém světě v projektu nazvaném Event Horizon Telescope. Jen díky mnoha pozorováním z různých míst planety a následnému sloučení naměřených dat bylo možné tuto fotografii pořídit. Vidíme ji vpravo na obrázku 4.55. Respektive samozřejmě vidíme jen její akreční disk, jehož světlo k nám prochází silně zakřivenou oblastí blízko černé díry, čímž dochází k výrazným zkreslením. Možná se vám nepozdává kvalita snímku, ale je nutné si uvědomit, že ač se jedná v našich lidských měřítkách o obrovský objekt (dosahující téměř velikost Sluneční soustavy), je nepředstavitelně daleko. Ředitel projektu EHT přirovnal pořízení snímku M87* k „vyfocení čtvrťáku na vzdálenost mezi New Yorkem a Los Angeles, a přitom dokážeme přečíst text na minci“.

Obrázek 4.55 Vlevo: Celkový pohled na černou díru M87* a její okolí pomocí satelitního rentgenového teleskopu Chandra X-Ray. Na obrázku je zřetelně vidět mohutný výtrysk hmoty dosahující do vzdálenosti \(1000\) světelných let (tj. asi setinu průměru Mléčné dráhy).
Vpravo: Detailní záběr na černou díru a její akreční disk získaný díky projektu Event Horizon Telescope. Zdroj: https://futurism.com/the-byte/black-hole-photo-amazing-zoom-out
Dnes už tedy černé díry nepatří jen do říše čiré teorie, ale jejich existence je obecně uznávána. Z tohoto pohledu žijeme ve velmi zajímavé době, protože právě projekty typu EHT případně detektory gravitačních vln otvírají v poslední době zcela novou kapitolu v poznávání černých děr. Prozatím je dokážeme pozorovat samozřejmě jen na velikou dálku, ale třeba se k nim lidstvo jednou dostane blíže. Na závěr tohoto bleskového seznámení s černými dírami si ukážeme, jak by to asi vypadalo, kdybychom do jedné opravdu spadli:
Video 4.56 Vizualizace pádu do černé díry.
Newton vs. Einstein
Strávili jsme už pěknou řádku stran snahou trochu proniknout do způsobu, jakým obecná teorie relativity popisuje gravitaci. Hodně jsme se při tom odkazovali na newtonovskou teorii gravitace, porovnávali tyto dvě teorie mezi sebou a prakticky vždy dávali přednost Einsteinově teorii jako té lépe popisující náš svět. To ale samozřejmě neznamená, že se přestaneme ve školách učit klasickou teorii gravitace a hned od začátku pojedeme relativisticky. Pokud jste středoškolskou kapitolou gravitace již prošli, pravděpodobně si vzpomenete, jak, vám co si čtete tento text možná ne, ale třeba některým vašim spolužákům, dělaly i v tomto případě výpočty problémy (a to je typická středoškolská látka jen špičkou ledovce plné klasické teorie a jejích možných aplikací). A teď si představte, že bychom místo toho nastoupili s diferenciální geometrií, metrikou, derivacemi apod.
Relativní jednoduchost ale samozřejmě není ten hlavní důvod, proč má newtonovská gravitace ve škole své místo. Ona totiž v pro nás běžných podmínkách funguje zatraceně dobře. Navíc například i takový jednoduchý pohyb v gravitačním poli jako je šikmý vrh se dá klasickou fyzikou vyřešit na pár řádcích, zatímco relativisticky už si člověk celkem započítá. Ve slabém (tj. pro nás běžném) gravitačním poli budou navíc výsledky obou teorií od sebe prakticky nerozlišitelné. Proto je a bude klasická teorie gravitace tou „hlavní“ na Zemi i pro vesmírné lety v okolí Země a dále po naší soustavě (malou výjimkou jsou zmíněné relativistické korekce v satelitech globální navigace apod.).
Z experimentů víme, že OTR dává správnější předpovědi, dokonce předpovídá celou řadu nových dnes již naměřených efektů. Ale v situacích, kdy není potřeba používat relativitu, zcela samozřejmě sáhneme po starém dobrém Newtonově gravitačním zákonu. Rozhodně se tedy nejedná o konflikt Newton vs. Einstein, jak říká nadpis, ale nejdřív Newton, potom Einstein. Vědecký pokrok je možný díky návaznosti práce současných vědců na ty předcházející, ať už ji rozšiřují či vyvrací. Sám Newton kdysi napsal o své práci: „Pokud jsem viděl dále, bylo to proto, že jsem stál na ramenech obrů.“ Byla to pravda v 17. století a je to o to více pravda i dnes.
Vztah mezi oběma teoriemi můžeme hezky ilustrovat následujícím smyšleným příběhem vypůjčeným ze skvělé knihy [ii]. Představme si dva antické cestovatele, kteří se nezávisle na sobě rozhodnou podniknout dalekou cestu na sever. Každý vyrazí ze svého rodného města (pro jednoduchost předpokládejme, že obě města leží na rovníku - obrázek 4.57). Oba tak putují prakticky po svém vlastním poledníku, což ale cestovatelé nevědí, protože jim zatím není známo, že je Země ve skutečnosti kulatá. Řečeno trochu návodně, nemají ponětí o zakřivení zemského povrchu.
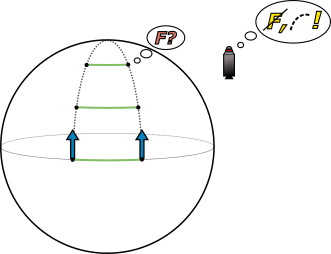
Obrázek 4.57 Ilustrace příběhu o dvou cestovatelích. Čím více se blíží k severnímu pólu, tím rychleji se vzdálenost mezi nimi zkracuje. Bez znalosti geometrie planety nutně dochází k závěru, že mezi nimi působí jakási přitažlivá síla.
Během své cesty si mezi sebou posílají zprávy po poslech a díky tomu si časem všimnou, že jejich vzájemná vzdálenost se zmenšila. A čím víc se dostávají na sever, tím je nejen jejich vzdálenost stále menší, ale zároveň se zmenšuje rychleji. Přemýšlí o tomto zvláštním zjištění a dochází k faktu, že mezi nimi musí působit nějaká síla, která je navzájem přitahuje a čím severněji jsou, tím je tato síla větší. Neví, co tu sílu způsobuje, ale zjevně pozorují její účinky. Mohou provádět různé experimenty a zkoumat, na čem všem velikost této přitažlivé síly závisí. Z experimentů vyvodí teoretické vztahy a na jejich základě vytvoří předpovědi pro jiné situace atd.
My samozřejmě víme, že zde žádná přitažlivá síla nepůsobí. Cestovatelé se k sobě přibližují čistě na základě pohybu na zakřiveném povrchu. Aby si tohle ale uvědomili, museli by mít dobrou představu o tvaru Země. Buďto by se museli vznést vysoko do oblak nebo ještě lépe na oběžnou a podívat se na Zemi z výšky, tedy ze třetího rozměru, anebo by museli zakřivení Země odhalit na základě precizních pozorování a měření přímo na povrchu (vzpomeňme na Erathosténa z Kyrény a jeho měření délky stínu ve stejný čas na různých místech). S gravitací a prostoročasem je to zrovna tak. Akorát se nedokážeme podívat na prostoročas z vyššího rozměru, nedokážeme „vidět“ jeho zakřivení. Musíme vystačit se stále přesnějšími měřeními jeho vnitřní geometrie.
Einsteinova teorie relativity posunula lidské chápání gravitace výrazně kupředu. Od přitažlivé síly k zakřivenému prostoročasu je to dost velký myšlenkový skok. Zároveň si ale musíme uvědomit, že OTR cesta za poznáním gravitace nekončí. Již jsme se zmiňovali o limitech obecné relativity v souvislosti s černými dírami. Například ale také zatím nedokážeme odpovědět na otázku, proč vlastně kolem sebe hmotná tělesa zakřivují prostoročas. Relativita toto zakřivení pouze popisuje, ale nevysvětluje. Jak to tak na světě bývá, snaha najít odpovědi ohledně povahy světa s sebou prakticky vždy přináší nové otázky. Rozhodně se tak nemusíme bát, že by budoucí generace neměly co zkoumat.
Na tomto místě prozatím naše povídání ukončíme. Říkáme prozatím, protože do budoucna je v plánu tento text stále rozšiřovat, a to nejenom ve středoškolské, ale i plně vysokoškolské úrovni. Témat, o kterých se dá psát, je stále dost, například gravitační vlny nebo kosmologie. Díky vám, kteří jste se dočetli až sem na konec. Doufáme, že vám text byl k užitku, že alespoň částečně naplnil svůj účel i vaše očekávání a poodhalil vám základní myšlenky obecné teorie relativity. Nyní snad už máte lepší představu o tom, proč je podle fyziků gravitace zakřivením prostoročasu.
Máte-li k textu nějaké připomínky, dotazy či návrhy na zlepšení, budeme rádi, když nám je zašlete na matej.rys gmail.com.
gmail.com.
Shrnutí kapitoly 4.3
K vypočítání metriky zakřiveného prostoročasu na základě rozložení hmoty a energie slouží tzv. Einsteinovy rovnice.
Prostoročas kolem sféricky symetrického nerotujícího tělesa o hmotnosti \(M\) popisuje Schwarzschildovo řešení Einsteinových rovnic. Protože pohyb ovlivněný čistě gravitací kolem takového tělesa je vždy rovinný, stačí nám soustředit se na rovinný řez tímto prostoročasem, jehož metrika je \begin{equation*} (\text{d}s)^2=-\left(1-\frac{2GM}{c^2r}\right)c^2(\text{d}t)^2+\frac{(\text{d}r)^2}{1-\frac{2GM}{c^2r}}+r^2(\text{d}\varphi)^2, \end{equation*} kde používáme Schwarzschildovské souřadnice \(t,r,\varphi\). \(t\) má význam vlastního času stojícího pozorovatele nekonečně daleko, \(r\) je radiální souřadnice, ale nemá význam vzdálenosti od středu, protože v radiálním směru dochází k deformaci prostoru. \(\varphi\) je stejná úhlová souřadnice, jako se vyskytuje např. v polárních souřadnicích, protože v tečném směru k deformaci nedochází.
Výraz \(2GM/c^2\equiv r_\text{S}\) se nazývá Schwarzschildův poloměr. Kromě univerzálních konstant závisí čistě na hmotnosti centrálního tělesa. Všechny běžné astronomické objekty jako planety, hvězdy apod. mají rozměry bezpečně větší než je jejich \(r_\text{S}\). Pokud bychom nějaký objekt stlačili na menší rozměr než je \(r_\text{S}\), vznikne černá díra.
Prostorovou deformaci Schwarzschildova prostoročasu můžeme vizualizovat pomocí tzv. diagramu vnoření, kdy vytvoříme plochu, jejíž zakřivení má stejnou velikost jako zakřivení ekvatoriální roviny Schwarzschildova prostoročasu. Vzniklá plocha se nazývá Flammův paraboloid a jedná se o typický trychtýřovitý tvar, který známe z mnoha ilustrací spojených s obecnou relativitou a prostoročasem.
V silnějším gravitačním poli plyne čas pomaleji. Mluvíme o gravitační dilataci času. Například mezi plynutím souřadnicového času \(t\) a vlastního času \(\tau\) pozorovatele stojícího na nějaké konkrétní hodnotě souřadnice \(r\), platí \begin{equation*} \text{d}\tau= \sqrt{1-\frac{r_\text{S}}{r}}\text{d}t. \end{equation*}
Gravitační dilatace času (ale i ta kinematická) se uplatňuje v globální satelitní navigaci, protože satelitům na oběžné dráze plyne čas trochu jinak, než nám na Zemi. To je problém, protože určení polohy závisí na časovém rozdílu mezi vysláním signálu satelitem a jeho zachycením na Zemi. Systém proto musí při výpočtech dělat relativistické korekce, aby rozdíl v plynutí času vykompenzoval.
Dalším relativistickým efektem je stáčení eliptických drah obíhajících těles. Poprvé byl tento efekt pozorován u Merkuru, kde mluvíme o stáčení perihelia (bodu na oběžné dráze nejbližšího Slunci). I když velká část tohoto stáčení je vysvětlována gravitačním působením ostatních planet, zbývající část byla vysvětlena až obecnou relativitou.
Již od roku 1919 víme díky Eddingtonově experimentu, že trajektorie světla je v gravitačním poli ohýbána, a to v souladu s předpovědí OTR. Jedním z důsledků je jev zvaný gravitační čočka, kdy mezi námi a vzdáleným objektem leží další hmotný objekt, jehož gravitace zakřivuje trajektorii kolem procházejících paprsků. Výsledkem je pozorování několika obrazů vzdálenějšího tělesa a v případě přesného zákrytu můžeme pozorovat i roztažení obrazu do tzv. Einsteinova prstence.
Černá díra je těleso o rozměrech menších než je jeho Schwarzschildův poloměr. Díky extrémní hustotě zakřivuje okolní prostoročas natolik, že z oblasti pod tzv. horizontem událostí (\(r\le r_\text{S}\)) neunikne ani světlo, natož jakékoli hmotné těleso. Dnes již nejsou černé díry pouze hypotetické, máme už celou řadu astronomických pozorování, která existenci černých děr prakticky potvrzují. Singularity uvnitř černých děr poukazují na limity obecné relativity a potřebu jejího sloučení s kvantovou mechanikou, což je stále ještě nedořešený problém.
I když je OTR správnější než Newtonova gravitační teorie ve smyslu souhlasu s experimentem, stále má smysl se klasickou teorií zabývat, protože ve slabém gravitačním poli (tj. v naprosté většině situací na Zemi i v celé Sluneční soustavě) se jejich předpovědi překrývají a klasická teorie je výrazně jednodušší na výpočty i představu. OTR je třeba použít v případě silných gravitačních polí (například v blízkosti neutronových hvězd či černých děr) a v kosmologii, anebo pokud se zabýváme čistě relativistickým efektem, jako je třeba dilatace času.