Část 4: Obecná relativita
Konečně se dostáváme k základním myšlenkám obecné teorie relativity (OTR). Vysvětlíme si, proč se jí říká obecná, jak souvisí s tou speciální, a proč se týká především gravitace. Ona totiž základní myšlenka celé OTR, jak se můžeme dočíst prakticky v každé populární knize věnované této teorii, se dá shrnout do velmi stručné věty: „Gravitace je zakřivení prostoročasu“. Naším hlavním úkolem tedy bude pochopit, co tato věta přesně znamená. A protože prostoročas jsme si už představili v předchozí části, budeme se nyní bavit zejména o zakřivení. Samozřejmostí jsou také nejdůležitější důsledky obecné relativity, díky kterým je možné ji experimentálně ověřovat. Tato část bude méně matematická než ty předcházející, protože naprostá většina matematického aparátu OTR spadá do vysokoškolské matematiky, zejména diferenciální geometrie a tenzorového počtu. Protože není naším úmyslem utopit čtenáře v nové matematice, která je jen těžko pochopitelná bez předchozího (často i několikaletého) studia matematické analýzy a algebry, budeme dávat větší důraz na fyzikální myšlenky a vhodné analogie. Na druhou stranu, protože zcela bez matematiky se fyzika pořádně dělat nedá, tu a tam narazíme na trochu komplikovanější výpočty, které mohou středoškoláci alespoň trochu znát z vyšších ročníků nebo výběrových matematických seminářů. Takové příklady jsou pak většinou schované v rozbalitelných záložkách, aby si je zájemci mohli prohlédnout, ale aby zároveň zbytečně nenarušovaly zbytek textu.
Vývoj moderní teorie relativity připomíná výklad ve škole, kde učitel při probírání látky začne jednoduchým speciálním případem a následně ho použije jako odrazový můstek ke složitějšímu a obecnějšímu závěru. Stejným způsobem formuloval Einstein nejprve speciální teorii relativity, kde pracujeme s inerciálními vztažnými soustavami. Pokud bychom měli vystihnout obecnou teorii relativity několika slovy, řekli bychom, že je to teorie gravitace. Zabývá se gravitací jako důsledek snahy o zobecnění závěrů speciální relativity. Inerciální vztažné soustavy, které si STR vybírá k popisu světa kolem nás, jsou spjaty s dosti speciální třídou pozorovatelů. Pro ně byl postulován princip relativity i princip konstantní rychlosti světla ve vakuu. Zcela oprávněně bychom se pak mohli ptát, zda nejdou relativistické úvahy o různých pozorovatelích a jejich vztažných systémech zobecnit tak, aby zahrnovaly i neinerciální pozorovatele. Vždyť skutečnost, že se někdo vůči nám pohybuje se zrychlením, ještě neznamená, že je jeho popis méně platný než ten náš. Zároveň se ukazuje, že na rozdíl třeba od elektrické síly, gravitační síla nejde nijak odstínit, čímž narušuje jakýkoli inerciální systém ve svém dosahu a dělá ho neinerciálním. Je tedy nutné se s neinerciálními systémy vypořádat přímo.
4.1 První úvahy
Ještě než ale zodpovíme otázku ohledně souvislosti neinerciálních soustav a gravitace, měli bychom se podívat na důvody, proč jsme se gravitací ve speciální relativitě vůbec nezabývali. Ty jsou v zásadě dva. Prvním z nich je tzv. okamžité působení na dálku.
Klasická mechanika pohlíží na gravitaci jako na přitažlivou sílu, která se řídí Newtonovým gravitačním zákonem. Ze střední školy víme, že velikost gravitační síly mezi dvěma sféricky symetrickými tělesy o hmotnostech \(m_1\) a \(m_2\), která jsou od sebe vzdálena \(r\), je \begin{equation*}\label{4.1}\tag{4.1} F_g=G\frac{m_1m_2}{r^2}, \end{equation*} kde \(G\) je Newtonova gravitační konstanta (někdy značena také \(\kappa\)). Směr této síly je vždy dán spojnicí obou těles. Vzorec \eqref{4.1}, který velice dobře vysvětluje pohyb planet v naší sluneční soustavě a dodnes je používán v situacích, kdy není zapotřebí používat teorii relativity (například pro slabé gravitační pole), je ale v zásadním rozporu s STR. Podle \eqref{4.1} na sebe působí tělesa na dálku gravitační silou, a pokud se například poloha jednoho z těles změní, změní se okamžitě síla působící na druhé těleso, i kdyby bylo stovky světelných let daleko. Informace o tělese se tedy šíří nekonečně rychle (to znamená okamžitě) a to se nám nelíbí díky úvaze o kauzalitě na konci třetí části textu. Uvažme, že s dostatečně citlivými přístroji bychom ovlivněním jednoho tělesa mohli v principu okamžitě posílat informace „gravitační morseovkou“ přes obrovské vzdálenosti.
Sílu tohoto rozporu můžeme ukázat i následujícím způsobem. Představme si například, že by naše Slunce najednou zničehonic zmizelo. Podle klasické teorie by gravitační působení na Zemi obíhající po téměř kruhové dráze okamžitě přestalo a my nic netušící pozemšťané bychom sledovali (pokud bychom si toho stačili všimnout), jak naše planeta odlétá po tečně ke své původní trajektorii, jako když se točí závažím na šňůře, a ta se najednou utrhne. Mezitím by k nám stále ještě přicházelo světlo ze Slunce, takže by ani nebylo jasné, co vychýlení naší planety z orbity způsobilo. Na druhou stranu, podle speciální teorie relativity se veškeré informace šíří maximálně rychlostí světla. Podle toho by po zmizení naší hvězdy Země ještě něco málo přes osm minut klidně pokračovala po své normální dráze a teprve pak by se vydala vstříc mrazivé prázdnotě okolního vesmíru. Současně by k nám dolétly poslední sluneční paprsky vyslané před zmizením Slunce, a tak bychom, tváří v tvář globální katastrofě, alespoň věděli, co je její příčinou.
Ponurost tohoto příkladu stranou, chceme-li se držet našich úvah o relativitě, budeme patrně muset pozměnit náš náhled na gravitaci. Zdá se být nanejvýš podivné, že by část fyziky měla být omezena rychlostí světla, zatímco jiná část by „fungovala“ bez tohoto omezení. Proto nám stojí za to se alespoň znovu zamyslet nad gravitací z relativistického hlediska.
Slabý princip ekvivalence
Gravitace má na rozdíl od ostatních interakcí jednu zvláštní vlastnost, se kterou klasická fyzika, a spolu s ní i výklad na střední škole, pracuje, ale nijak ji nevysvětluje. Oproti například elektrické síle působí gravitace na všechny předměty stejně. Obvyklá formulace zní, že všechna tělesa padají se stejným zrychlením. Možná jste viděli demonstrační pokus s padáním předmětů v trubicích či celých místnostech s odčerpaným vzduchem (protože odpor vzduchu tuto univerzálnost narušuje), případně slavné video z povrchu Měsíce, kde astronaut najednou pustí ptačí pero a kladivo ze stejné výšky a oba předměty dopadnou ve stejný okamžik. Matematicky se tato univerzalita projeví, když budeme vyšetřovat pohyb tělesa v gravitačním poli (obrázek 4.1). Podle 2. Newtonova zákona dáme do rovnosti hmotnost předmětu krát jeho zrychlení a působící sílu, v tomto případě gravitační. Velikostně je \begin{equation*} ma=\frac{GmM}{r^2}\Rightarrow{}a=\frac{GM}{r^2}, \end{equation*} \(M\) je zde hmotnost zdroje gravitace (Země, případně Měsíc apod.). Z toho plyne, že různé předměty s libovolnou hmotností, pokud jsou stejně daleko od středu Země, padají v daném místě se stejným zrychlením.

Obrázek 4.1 K pohybové rovnici tělesa v gravitačním poli.
Tato úvaha má ale jeden zásadní nedostatek. Na levé a pravé straně rovnice totiž vystupují hmotnosti ve zcela jiném významu. Druhý Newtonův zákon \(\vec{F}=m_s\vec{a}\) mluví o tzv. setrvačné hmotnosti a je pro ni prakticky definičním vztahem (pro odlišení jsme ji zde označili \(m_s\)). Je to konstanta úměrnosti mezi silou působící na těleso a zrychlením, které je tělesu udělováno. Čím větší je hmotnost předmětu, tím větší síla je třeba na to, abychom mu udělili dané zrychlení. Naproti tomu hmotnost vystupující na pravé straně rovnice nám říká, jak moc je dané těleso gravitačně přitahováno a zároveň jak silně přitahuje ostatní hmotná tělesa. Možná jste se už setkali s tzv. Coulombovým zákonem. Ten je v jistém slova smyslu elektrickým ekvivalentem gravitačního zákona \eqref{4.1}, protože udává velikost elektrické síly, kterou na sebe působí dva bodové náboje o velikostech \(q_1\) a \(q_2\) opět ve vzájemné vzdálenosti \(r\): \begin{equation*} F_e=\frac{1}{4\pi\epsilon}\frac{q_1 q_2}{r^2}. \end{equation*} Konstanta \(\epsilon\) se nazývá elektrická permitivita a charakterizuje elektrické vlastnosti daného prostředí, nicméně pro nás nyní není důležitá. Inspirováni Coulombovým zákonem můžeme tedy hmotnost vystupující v gravitačním zákonu (označme ji jako \(m_g\)) chápat jako jakýsi gravitační náboj. Máme tak dvě principiálně odlišné veličiny a teprve naše experimenty nám mohou říci, zda se \(m_s\) a \(m_g\) rovnají a pokud ano, jestli tomu tak je pro všechna tělesa či částice.
Fakt, že se pro tělesa gravitační a setrvačná hmotnost rovnají, je experimentálně ověřován už od dob Galilea (také jemu je připisován výrok, že všechny věci padají k zemi se stejným zrychlením). Důmyslné mechanické experimenty s čím dál tím větší přesností potvrzují rovnost těchto dvou veličin, v případě pozemským experimentů až do řádu \(10^{-12}\). To znamená, že pokud by se setrvačné a gravitační hmotnosti zkoumaných předmětů přece jen lišily, bylo by to o méně než jednu desetimiliardtinu procenta. Byl také navržen experiment k provedení na oběžné dráze pomocí satelitu, který by tuto přesnost posunul až na \(10^{-18}\). I když to tedy zatím vypadá, že mezi oběma hmotnostmi nemusíme rozlišovat, je dobré si uvědomit, že jejich rovnost není automaticky zaručena.
Tvrzení o rovnosti gravitační a setrvačné hmotnosti nazýváme slabým principem ekvivalence. Jedná se o důležitý předpoklad pro teorii relativity, a proto je se stále rostoucí přesností ověřován. Jeho důsledkem je právě jistá univerzálnost gravitace, tedy závěr, že gravitace uděluje tělesu zrychlení nezávisle na jeho hmotnosti či materiálu. Například pro elektrickou sílu to pravda není. Pokud bychom Coulombův zákon použili pro případ ekvivalentní k obrázku 4.1, tedy že máme zdroj elektrického pole s nábojem \(Q\) a od něj ve vakuu ve vzdálenosti \(r\) jiné těleso s nábojem \(q\) a hmotností \(m\), dostáváme pro zrychlení tohoto tělesa \begin{equation*} ma=F_e=\frac{1}{4\pi\epsilon_0}\frac{qQ}{r^2}\Rightarrow{}a=\frac{q}{m}\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}. \end{equation*} Vidíme, že zrychlení nabitého tělesa závisí na poměru jeho náboje a hmotnosti, speciálně závisí na jeho náboji, takže není pravda, že by byla všechna nabitá tělesa ovlivňována elektrickým polem stejně.
Existuje ale třída sil, které fungují podobně univerzálně jako gravitace. Jsou to tzv. setrvačné síly (nazývány také zdánlivé nebo nepravé). Zavádějí se na škole většinou v souvislosti s neinerciálními systémy. Nazýváme je nepravé, protože na rozdíl od např. elektrické síly nejsou způsobeny reálnou fyzikální interakcí. Jejich efekt pozorujeme, pokud se nacházíme v soustavě se zrychlením. Pozor na to, že může jít o jakékoli zrychlení, nejenom zvyšování a snižování velikosti rychlosti, ale také zatáčení nebo i rotaci. Například vezeme-li se na kolotoči, cítíme působení odstředivé síly, která nás chce vytáhnout ven z kolotoče (působí směrem od středu otáčení). Zároveň ale na kolotoči nevidíme, co přesně tuto sílu způsobuje. Naproti tomu náš kamarád stojící na zemi vidí, že naše tělo má tendenci vypadnout z kolotoče a pokračovat po tečně k trajektorii otáčivého pohybu. Je to naše setrvačnost (tendence pohybovat se rovnoměrně přímočaře), která nás „vytrhává“ z kolotoče, a tím se nám zdá, že na nás působí odstředivá síla. To si můžeme sami snadno potvrdit tak, že když roztočíme závaží na provázku a najednou provázek pustíme, závaží díky své setrvačnosti odletí ve směru tečny k původní trajektorii kružnici, tedy po přímce.
Pro velikost odstředivé síly platí \(F_o=m\omega^2r\), kde \(\omega\) je úhlová rychlost otáčení a \(r\) je vzdálenost od osy otáčení. Podobně jako dříve u gravitačního zrychlení můžeme snadno najít vztah pro zrychlení odstředivé \(a_o\), které nám odstředivá síla způsobuje. Podle druhého Newtonova zákona musí platit \(F_o=ma_o\), takže čistě srovnáním dvou předchozích vztahů vychází \(a_o=\omega^2r\). Odstředivé zrychlení je tedy, podobně jako u gravitačního zrychlení, stejné pro všechny předměty nehledě na jejich hmotnosti, důležitá je u tělesa jen jeho poloha – v tomto případě vzdálenost od osy otáčení.
Obecně platí, že jakékoli setrvačné zrychlení v neinerciální soustavě působí vždy proti směru zrychlení této soustavy. U zmíněného pohybu na kolotoči zatáčíme díky tzv. dostředivému zrychlení (jak víme z analýzy pohybu po kružnici), setrvačné zrychlení je ale odstředivé. Podobný argument platí i pro další nepravé síly. Na videu níže auto prudce zpomaluje nárazem, jeho zrychlení v soustavě spojené se zemí tedy míří proti směru jízdy. Pohyb figuríny z hlediska auta a zároveň i její setrvačné zrychlení je ale dopředu. Můžete si také sami zkusit rozmyslet, že velikost zrychlení soustavy jako celku (prudce zastavující auto) a setrvačného zrychlení, které pozorujeme uvnitř ní (trhnutí figuríny dopředu z hlediska auta) mají sice opačný směr, ale stejnou velikost.
Video 4.2a: Při pohledu z venku vidíme, že figurína je po nárazu "vymrštěna" proti volantu díky své setrvačnosti, ne nějakou vnější silou, jak se tomu může zdát z pohledu pozorovatele uvnitř auta.
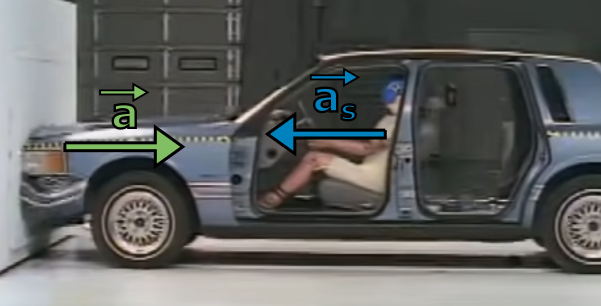
Obrázek 4.2b Záběr z videa 4.2a výše. Stěna působí na auto silou a tím mu uděluje zrychlení proti směru pohybu (brzdí ho). Auto se tím stává neinerciální vztažnou soustavou a začnou v něm z pohledu pasažéra působit setrvačné síly proti směru zrychlení auta (dopředu).
Nabízí se tedy otázka, zda je vůbec gravitace pravá síla, jak to tvrdí klasická mechanika. Není možné, že nám gravitace připadá jako reálná síla jen proto, že na ni nahlížíme ze špatného úhlu pohledu? Pokud by to ale nebyla síla v pravém slova smyslu, tak co je to? K pochopení tohoto problému potřebujeme blíže prozkoumat účinky gravitace na svět kolem nás. Jak musíme pozměnit naše chápání prostoročasu zavedeného speciální relativitou v přítomnosti gravitace?
Lokální inerciální systémy
Již jsme zmínili, že přítomnost gravitace nám striktně vzato znemožňuje vytvářet inerciální systémy, což je hlavní důvod, proč STR a gravitace nejdou dobře dohromady. Jak jsme totiž viděli v minulé části, STR je celá o inerciálních systémech. Ty jsou definovány pomocí volných částic, tedy takových, na které nepůsobí žádná výsledná síla, a vykonávají tak rovnoměrný přímočarý pohyb. V přítomnosti gravitace ale na všechny hmotné částice, klasicky řečeno, působí gravitační síla.
Poznámka 4.1
Zde je třeba si předem něco vyjasnit, abychom se vyhnuli případnému nedorozumění. V minulých částech jsme, tak jak je zvykem v klasické fyzice i ve speciální relativitě, považovali soustavu spojenou se zemí za dostatečně přibližně inerciální v situacích, kdy bylo rozumné zanedbat rotaci a další pohyby planety vůči například Slunci. Zároveň jsme neuvažovali vliv gravitace. To nám třeba u aut jedoucích po vodorovné silnici nebo u části v urychlovači, jejichž svazek je kolimován elektrickým polem, tzn. v případech, kdy je gravitace vykompenzována nějakou jinou působící silou, docela dobře prošlo. Nyní se už ale nebudeme takto gravitaci vyhýbat, protože právě tu chceme „relativisticky“ zkoumat. Jak uvidíme, bude to mimo jiné znamenat, že budeme muset přehodnotit některé naše dosavadní úvahy, například o tom, co vlastně je inerciální soustava a co není. Nic naplat, podobně jako některé zavedené klasické pořádky boří speciální relativita, i ta obecná nás donutí se na některé věci dívat jinak než dosud. Nechceme ale zatím dopředu zbytečně nic prozrazovat, takže tuto poznámku berte jen jako takové obecné upozornění. A pokud vám bude někdy připadat, že si s předchozími částmi trochu protiřečíme, připomeňte si, že se jedná o nový úhel pohledu.
Tento problém nám například s elektrickou silou nevznikne, protože ta jde teoreticky odstínit například pomocí Faradayovy klece, jejíž fungování je založeno na existenci dvou druhů elektrických nábojů, kladného a záporného, jejichž působení se mohou navzájem vyrušit. U gravitace máme ale jenom jeden „náboj“ – hmotnost, takže odstínit gravitaci se nám žádnou bariérou nepodaří. Najednou nemáme jak realizovat inerciální systém. Anebo ano?
Představme si na moment, že se pohybujeme v raketě vesmírným vzduchoprázdnem daleko od zdrojů silových působení. Nemáme jak změřit vzdálenosti k jiným objektům, protože je nevidíme. Jsme zavřeni v naší kajutě, a nemáme přístup k žádnému ovládacímu prvku rakety. Dokážeme v takovém případě poznat, zda jsou motory rakety v chodu? Pokud ano, měla by se raketa pohybovat se zrychlením (řekněme vůči vzdáleným hvězdám). Ale pokud ne, a nepůsobí na ni tedy žádná síla, měla by se podle zákona setrvačnosti pohybovat rovnoměrně přímočaře a být, opět řekněme vůči vzdáleným hvězdám, inerciálním systémem.
Odpověď je snadná a už jsme na ni narazili v části o klasické relativitě. Vezměme jakýkoli předmět, co máme po kapsách našeho skafandru (řekněme tužku), a umístěme ho do prostoru tak, aby byl vůči nám v klidu. Pokud v klidu vůči nám zůstane, opravdu se můžeme hrdě prohlásit za inerciálního pozorovatele. Pokud se ale volný předmět vůči nám začne pohybovat navzdory našemu opatrnému vypuštění z relativního klidu (bude „zaostávat“ za zrychlující raketou), znamená to, že se pohybujeme se zrychlením a ani naše vlastní vztažná soustava nemůže být inerciální.
Zkuste si provést tento test sami. Vezměte do ruky nějaký předmět (ideálně takový, který se snadno nerozbije nebo jehož rozbití nebudete litovat) a pusťte ho z klidu z ruky. Pokud náhodou nejste při čtení tohoto textu ve stavu beztíže někde na oběžné dráze Země (což je v současné době sice možné, ale u běžného čtenáře vysoce nepravděpodobné), nejspíš vámi puštěný předmět spadl volným pádem na zem. Jinak řečeno, začal od vás zrychlovat. Vaše soustava tedy ve skutečnosti není inerciální. Klasicky si tuto situaci vysvětlujeme působením gravitační síly, která působí na volné těleso, a tím pádem není porušen první Newtonův zákon (ten mluví pouze o tělesech, na které působí nulová celková síla). Daný předmět stačí položit na stůl a pak jsou všechny síly vyrovnány, gravitační síla je kompenzována reakční silou stolu a těleso se nezačne pohybovat. Ale to je speciální případ. Chceme-li se zabývat širokou škálou fyzikálních situací, zejména různě pohybujícími se tělesy, jako ve speciální relativitě, najednou máme problém. Například trajektorie pohybujícího se inerciálního pozorovatele je přímka (myšleno vůči jinému inerciálnímu pozorovateli) a v gravitačním poli Země je prakticky nemožné se obecně po přímce pohybovat. Museli bychom se omezit jen na úzkou množinu případů. Vidíme tedy, že minimálně čistě teoreticky v gravitačním poli speciální relativitu používat nemůžeme. Přesto ale existuje cesta.
Provedeme společně ještě jeden jednoduchý experiment, ale pokud ho budete prakticky zkoušet, buďte, prosím, opatrní. Stoupněte si na židli, pohovku nebo menší stůl a psychicky se připravte seskočit na zem. Protože v tomto případě volný pád trvá velice krátce, budete pravděpodobně pokus muset opakovat víckrát (případně si můžete celou situaci nahrát na kameru). Seskočte na zem a své vybrané těleso z prvního pokusu si hned po začátku skoku pusťte ve výšce očí. Jak dopadl váš pokus? Pokud se vám povedlo mít při jeho puštění klidnou ruku, předmět by měl padat stejně s vámi, a proto bude z vašeho pohledu chvíli „viset ve vzduchu“ úplně stejně jako ve stavu beztíže. Tento výsledek by nás neměl příliš překvapit. Už víme, že všechna tělesa padají díky slabému principu ekvivalence se stejným zrychlením, takže (zanedbáme-li tření vzduchu) vy i předmět budete padat společně.
Představa padání volným pádem je pro člověka silně nepřirozená (a nejen díky vědomí, že na jeho konci nás čeká něco velmi nepříjemného). Z fyzikálního hlediska je ale volný pád velmi přirozený. Aniž byste nutně hned skákali z okna, představte si, že namísto seskočení ze židle nebo stolu volně padáte dlouho. Přitom zopakujeme svůj původní test inerciality naší soustavy vypuštěním tužky z klidu. Jak se bude pohybovat vzhledem k vám? Zůstane na místě. Zapomeňte na svištící vzduch kolem a jeho tření, které nám zbytečně komplikuje situaci (přece jen chceme dojít k nějakému univerzálnímu závěru o gravitaci a pád v atmosféře je z hlediska vesmíru přeci jen dost specifická situace). Zapomeňte na okolní budovy nebo zemi kdesi daleko pod vámi, která vám „tvrdí“, že se tužka pohybuje. Vzhledem k zemi ano, ale vzhledem k vám? Ne. Vaše klidová soustava je inerciální.
Trochu přesnější a názornější je použití akcelerometrů. Těmi je vybavena dnes už většina tabletů nebo chytrých telefonů (díky nim například telefon pozná, jak má natočit obrazovku, když ho otočíte na stranu). Pokud držíte v ruce v klidu správně kalibrovaný akcelerometr, bude ve svislém směru ukazovat hodnotu zrychlení přibližně \(9{,}8\:\text{m}\cdot{s}^{-2}\), tedy běžně používanou hodnotu pro tíhové zrychlení. Pokud rukou pohnete nahoru, ukazuje přístroj vyšší zrychlení. Pokud směrem dolů, měřené zrychlení se zmenší. Váš přístroj v tuto chvíli zažívá přesně to samé, co ve zmenšené míře zažíváme při cestě výtahem také my.
Poznámka 4.2
Pro naše další povídání bude užitečné si trochu osvětlit princip fungování takového akcelerometru. Jak vlastně pozná, že zrychluje? A jak je možné, že i když ho držíme v ruce v klidu, tak stejně naměří tíhové zrychlení? Obrázek 4.3a ukazuje jednoduchý mechanický model takového akcelerometru. Kulička je připojena ke dvěma pružinám, a dokud se akcelerometr nepohybuje se zrychlením, pružiny jsou stejně napnuté. Jakmile ale začne přístroj zrychlovat například doprava, kulička je díky své setrvačnosti z pohledu akcelerometru natlačena proti směru zrychlování, jedna pružina se více zmáčkne a druhá natáhne. Pak už nám stačí jen v principu odečíst ze zařízení, o kolik se kulička vychýlila, a díky znalosti tuhosti pružin bychom mohli určit působící setrvačnou sílu \(F_\text{s}\) (velmi podobně fungují pružinové siloměry, které možná znáte ze školy). Následně díky známé hmotnosti kuličky dostaneme i velikost setrvačného zrychlení kuličky. A ta je rovna, jak už víme, velikosti zrychlení celého přístroje. Matematicky můžeme celou situaci shrnout takto: \begin{equation*} a=\frac{F_\text{s}}{m}=\frac{ma_\text{s}}{m}=a_\text{s}. \end{equation*}

Obrázek 4.3a Mechanický model ukazující princip měření akcelerometru v jednom směru.
Video 4.3b: Popis principu elektronického akcelerometru MEMS používaného v mobilních zařízeních.
Asi všichni, kdo jsme kdy jeli výtahem (obzvláště staršího typu) známe ten pocit při rozjezdu nahoru, kdy se na okamžik cítíme „těžší“. Na malou chvíli musí naše kosti a svaly vynaložit víc námahy, aby nás udržely vzpřímené. Určitě vás někdy napadla otázka, proč se to děje. Když se výtah dává do pohybu směrem nahoru, má nenulové zrychlení, a je tím pádem neinerciální soustavou. Protože máme jako těleso původně v klidu tendenci setrvat na místě, v reakci na zrychlení výtahu na nás začne působit setrvačná síla. Už víme, že jak gravitační, tak setrvačná síla udělují předmětům zrychlení nezávisle na jejich hmotnosti. Pustíme-li pak libovolný předmět ve zrychlujícím výtahu z ruky, je velikost celkového zrychlení předmětu rovna součtu velikostí tíhového zrychlení \(g\) a setrvačného zrychlení \(a_\text{s}\), protože mají stejný směr, jak vidíme na obrázku 4.3c dole.

Obrázek 4.3c Skládání zrychlení působících na těleso (akcelerometr) ve zrychlujícím výtahu. V levém případě výtah zrychluje směrem nahoru, což způsobuje setrvačné zrychlení na předměty uvnitř směřující dolů (tělesa se snaží setrvat na místě). Má tím pádem stejný směr s tíhovým zrychlením, takže celkové zrychlení vůči výtahu (a také i zrychlení naměřené akcelerometrem) je větší. V pravém případě výtah zrychluje směrem dolů, setrvačné zrychlení je opačné oproti tíhovému a celkové zrychlení je tím pádem menší. Znázorněná zrychlení jsou pro větší přehlednost vykreslena vedle sebe, ve skutečnosti by měla všechna vycházet z těžiště tělesa.
Při rozjíždění výtahu vzhůru i náš akcelerometr naměří větší zrychlení. I my cítíme toto navýšení, na okamžik nám připadá, že jsme těžší, jinými slovy, že se tíhové zrychlení zvětšilo. Náš pocit ale netrvá dlouho, protože výtah velmi rychle dosáhne své cestovní rychlosti a dále pokračuje rovnoměrně přímočaře, takže setrvačné zrychlení zaniká a jak naše zdánlivá tíha, tak měření akcelerometru se vrací k normálu (obrázek 4.3c uprostřed).
Když dorazíme do námi zvoleného patra, výtah musí zabrzdit. To znamená brzdné zrychlení směřující tentokrát dolů a tím pádem setrvačná síla, která má tendenci nás udržet v pohybu nahoru, efektivně zmenšuje naší tíhu. Připadáme si lehčí, žaludek nám poskočí nahoru a akcelerometr na okamžik ukáže zrychlení nižší než \(g\), protože analogicky jako v prvním případě bychom dostali \(a=g-a_\text{s}\). Celkové zrychlení, které na nás působí, se tedy zmenší (obrázek 4.3c nahoře) oproti situaci, kdy je výtah v klidu.
Rozhodně se ale nezmenší tolik, jako kdyby náhle praskla všechna bezpečnostní lana výtahu a ten se s námi začal řítit do hlubin své šachty. Co bychom teoreticky zažili? Pokud bychom v nastalé panice měli čas na nějaké fyzikální zkoumání, všimli bychom si nejdříve, jak je veškerá naše tíha pryč a my se „odlepíme“ od podlahy. Výtah s námi padá volným pádem. I akcelerometr přijde o svoji tíhu a na displeji ukazuje nulové zrychlení stejně jako naše testovací tužka, která nám vypadla z kapsy. Mimochodem, pokud vás zajímá, jak takový akcelerometr funguje, stručný popis najdete v tomto anglickém videu. Bohužel, tato fascinující exkurze do inerciálního systému by velice rychle skončila nepříjemným koncem, protože dřív nebo později se nám do cesty postaví zem. V reálu samozřejmě stejně stavu beztíže v padajícím výtahu nedosáhneme, protože je výtah díky tření trochu brzděn, a tak nepadá nikdy přímo volným pádem. Co je ale důležitější, výtahy mají standardně nouzové brzdy, které se svým třením postarají o to, abychom neskončili rozplácnutí na dně výtahové šachty.
Ač se to tak může zdát, volně padající výtah není jen čistě teoretická úvaha. Například na univerzitě v Brémách v Německu existuje experimentální zařízení pro zkoumání fyzikálních jevů za stavu beztíže. Jedná se prakticky o vysokou věž s šachtou, ze které je možné vyčerpat vzduch a z výšky \(120\:\text{m}\) pouštět kapsle s experimentálním vybavením. A to není vše. Nad našimi hlavami neustále krouží reálný příklad volně padající inerciální soustavy – Mezinárodní vesmírná stanice neboli ISS (International Space Station). Ve skutečnosti je jím také jakýkoli jiný satelit na oběžné dráze naší planety, ale zůstaňme nyní u ISS.
Jak známo, ISS je orbitální stanice, na které se střídá mezinárodní posádka astronautů a kde se provádějí důležité experimenty testující nové technologie a zkoumá se vliv pobytu ve vesmíru na člověka či jiné organismy. Videa ze stanice jsou běžně dostupná na internetu. Mimořádně populární se stala videa kanadského astronauta Chrise Hadfielda, který je také prvním člověkem, který natočil hudební klip mimo naši planetu. Zájemci stačí napsat astronautovo jméno do internetového vyhledavače a objeví mnoho zajímavých videí, včetně například ukázky, jak se ve vesmíru čistí zuby. Mimochodem, zmíněný hudební klip se jmenuje Space Oddity, je tedy předělávkou slavné písně Davida Bowieho. Snadno se tak můžeme na vlastní oči přesvědčit o tom, jak se tělesa na palubě vesmírné stanice chovají. Předměty se vznáší, poletují kolem ve stavu beztíže, voda v klidu tvoří kulové kapky, astronauti nespí vleže, ale zavěšeni do spacáků. Na první pohled to vypadá, že ve vesmíru není gravitace (a bohužel se najdou tací, kteří si to opravdu myslí). To je ale omyl. I když se vzdáleností gravitační působení Země slábne, na orbitě ISS musí zcela jistě gravitace existovat, protože Měsíc, který je mnohem dál od Země než ISS, je zemskou gravitací držen na své oběžné dráze (konec konců to samé platí i pro ISS a všechny družice). Stejný argument můžeme použít pro gravitační působení mezi Zemí a Sluncem atd. Proč jsou tedy astronauti a vše na mezinárodní stanici ve stavu beztíže? Protože padají, i když ne v běžném slova smyslu.
Tradičně se stav beztíže na orbitě vysvětluje pomocí rovnosti velikostí gravitační a odstředivé síly. Pokud si orbitu ISS představíme jako přibližně kružnici, působí na stanici a tím pádem i posádku neustále odstředivá síla, která je stejně velká, ale opačná oproti gravitační síle, které zakřivuje dráhu stanice. Musí to tak být, protože kdyby jedna ze sil převážila, stanice by se buď zřítila na Zem, nebo odletěla pryč do okolního vesmíru. Existuje ale ještě jiné možné vysvětlení. Stanice pod sebou nemá žádnou podpěru, ani nemá permanentně zažehnuté motory, takže zde není nic, co by na první pohled bránilo jejímu pádu na povrch Země. Trik jak nespadnout na planetu spočívá právě v pohybu do strany, lépe řečeno v tečném pohybu.
V mechanice se například učíme o tzv. vodorovném vrhu, kdy dané těleso hodíme s nějakou počáteční rychlostí vodorovným směrem. Každý si může sám vyzkoušet, co se stane. Hodíme-li např. tenisákem vodorovně, jeho trajektorie zatočí směrem k zemi po křivce podobné parabole – obrázek 4.4 (a dá se ukázat, že bez tření vzduchu by to opravdu parabola byla). Tento pohyb typicky chápeme jako složený ze dvou na sebe kolmých jednodušších pohybů. Jedním z nich je volný pád, protože míček na začátku nemá žádnou rychlost směrem dolů a tím směrem ho urychluje tíhová síla. Na druhou stranu ve vodorovném směru na míček žádná síla a tím pádem ani žádné zrychlení nepůsobí (samozřejmě zde odhlížíme od tření vzduchu), takže vodorovná složka pohybu je čistě rovnoměrný přímočarý pohyb. Mimochodem, skutečnost, že můžeme nějaký složitější pohyb chápat jako složený z několika jednodušších je možné i otestovat. V populární rovině si to vyzkoušela nám již známá dvojice Bořičů mýtů.


Obrázek 4.4 Nahoře: Momentka z programu Tracker používaného pro videoanalýzu pohybu těles. Červené body jsou zachycené polohy tenisového míčku při vodorovném vrhu. Tyrkysové a fialové body jsou průměty jednotlivých poloh do vodorovného a svislého směru. Ve vodorovném směru pozoruje rovnoměrný pohyb, svislé body korespondují se zrychlujícím se volným pádem.
Dole: Zachycení celého letu.
Využijme nyní princip nezávislosti pohybů, abychom analyzovali přibližně kruhovou oběžnou dráhu ISS. Obíhání stanice se skládá ze dvou na sebe kolmých pohybů, volného pádu způsobeného gravitačním přitahováním k planetě a tečného rovnoměrného pohybu. I když se oba pohyby dějí najednou, můžeme si je představit separátně. Stanice se posune kousek v tečném směru a pak spadne kousek dolů k planetě. Pak se opět posune kousek do strany a opět dolů (obrázek 4.5). Tečná rychlost stanice musí být přesně tak velká, aby se její trajektorie uzavřela do kružnice. Z Newtonova gravitačního zákonu můžeme snadno odvodit vzorec pro tuto, tzv. kruhovou rychlost: \begin{equation*} v_k=\sqrt{\frac{GM}{r}}, \end{equation*} kde \(r\) je poloměr oběžné dráhy (tj. vzdálenost od středu kulového tělesa o hmotnosti \(M\), které obíháme). Ze vzorce je dobře patrné, že pro vzdálenější orbity vychází menší kruhová rychlost, protože gravitace se vzdáleností slábne, a proto není třeba se pohybovat tak rychle.
Z druhé kapitoly už víme, že rovnoměrný pohyb neovlivňuje fyzikální situaci v naší soustavě, takže dění na stanici musí probíhat stejně, jako by pouze padala volným pádem. A protože už víme, že ve volně padající soustavě nastává stav beztíže, je tím naše vysvětlení kompletní.
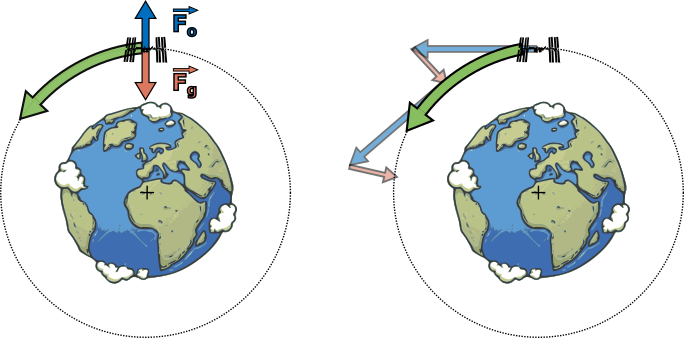
Obrázek 4.5 Vlevo: Stav beztíže na palubě mezinárodní vesmírné stanice si standardně vysvětlujeme rovností gravitační a odstředivé síly na palubě (jedná se o neinerciální soustavu).
Vpravo: Alternativně můžeme stav beztíže vysvětlit rozložením oběžného pohybu na dvě složky, volný pád, díky kterému nastává stav beztíže, a tečný pohyb konstantní rychlostí.
Poznámka 4.3
Možná vám připadá zvláštní, že posádka ISS považuje svou loď za inerciální soustavu, zatímco například z povrchu planety jasně vidíme, že se stanice pohybuje se zrychlením (mění směr své rychlosti), a z našeho pohledu by tudíž měla být neinerciální soustavou. To je rozpor, který je potřeba vyřešit. V části o klasické relativitě jsme si rozmysleli, že pokud je naše soustava inerciální, pak je každá další soustava, která se vůči nám pohybuje rovnoměrně přímočaře, také inerciální. Neinerciální soustavy jsou pak typicky ty, které vůči nám mají nenulové zrychlení. Jak ale vnímá situaci pozorovatel z té zrychlené soustavy?
Pro názornost si představme dvě kosmické lodi, Andromedu a Betelgeuse, které se potkají v prázdném vesmíru. Andromeda pluje prázdnotou s vypnutými motory. Jak už víme, je v tom případě inerciální soustavou a žádný experiment na palubě nedokáže rozlišit, zda se ve skutečnosti pohybuje nebo ne. Betelgeuse má motory zapnuté, takže se pohybuje vůči Andromedě se zrychlením. Na palubě působí setrvačné síly stejně jako třeba ve zrychlujícím automobilu – například je posádka tlačena do sedaček proti směru zrychlení apod. I kdyby tedy posádka Betelgeuse nevěděla, že má zapnuté motory, dokáže to snadno poznat podle chování těles na palubě včetně jejich vlastního pocitu. Není proto pochyb o tom, která z lodí je inerciální soustavou a která neinerciální. Nicméně podíváme-li se na situaci očima posádky Betelgeuse, my jsme samozřejmě vůči sobě v klidu a je to Andromeda, kterou vidíme se pohybovat se zrychlením. Závěrem této úvahy je, že i inerciální soustavy mohou být někým vnímány jako zrychlené. Typicky proto, že daný pozorovatel se sám pohybuje se zrychlením.
Vrátíme-li se k příkladu s ISS a pozorovatelem na Zemi, dostáváme velmi zvláštní výsledek. Je-li ISS inerciální soustavou (a sami se můžete podívat na již zmíněná videa ze stanice, kde opravdu například puštěné věci zůstávají viset na místě ve vzduchu nebo pokračují v rovnoměrném přímočarém pohybu) a odpovídá tedy Andromedě z předchozího odstavce, bude pozorovatel na Zemi odpovídat lodi Betelgeuse – je zrychlený. To je ale velmi zvláštní, protože na Zemi jsme přece v klidu, no ne? (Připomeňme, abychom předešli zmatení, že nyní vůbec neuvažujeme pohyb způsobený otáčením Země kolem své osy nebo obíháním Slunce – celá tato úvaha by fungovala, i kdyby byla Země zcela nehybná.)
Stojíme-li nohama pevně na zemi, klasický pohled na věc říká, že na nás působí dvě síly – gravitační a reakční síla podložky, která tu gravitační vyrovnává, díky čemuž jsme v klidu. Již jsme si ale na začátku této kapitoly rozmysleli, že ačkoli často soustavu spojenou se zemí považujeme za inerciální v situacích, kdy nepotřebujeme uvažovat účinek gravitace, podle našeho nového pohledu to inerciální soustava není. Důkazem byl jednoduchý pokus s vypuštěním předmětu z ruky. Nezůstane vůči nám v klidu, tak jak by se to stalo bez přítomnosti gravitace, ale začne zrychlovat k zemi volným pádem, dokud na ni nenarazí a nezačne na něj také působit reakční síla podložky. Podle této úvahy jsme tedy opravdu na zemi ve stejné situaci, jako posádka Betelgeuse. Naše soustava je zrychlená. Jistě si teď řeknete, že přece jenom je tu ale rozdíl, že posádka zrychlené lodi jasně cítí setrvačné síly působící proti směru pohybu, například již zmíněné tlačení do sedaček. To vy ale cítíte také. Ať už v tuto chvíli stojíte, sedíte či ležíte, je zde ta všude přítomná síla, která vás tlačí k zemi, do židle či do sedačky. Jen si ji neuvědomujete, protože jste na ni celý život zvyklí, vaše tělo se evolučně vyvinulo tak, aby ji překonávalo.
Můžeme si zde pomoci malou analogií. Představte si, že vás unáší proud v řece. Dokud se necháváte unášet, žádný tlak tekoucí vody na sobě necítíte, protože se pohybujete spolu s ní. Pak ale narazíte na velký kámen vyčnívající nad hladinu. Proud vody vás na něj přitiskne a vy cítíte tlak kamene, který je reakcí na vaše tlačení na něj. Není to ale tak hrozné a na ten tlak si poměrně rychle zvyknete a už ho ani moc nevnímáte. Vůči kamenu jste v klidu, zatímco vše kolem je strháváno proudem, dokud to třeba samo nenarazí na další kámen. Samozřejmě se nesnažíme tvrdit, že gravitace je to samé jako tekoucí voda v řece, ale určitá podobnost zde je. Jen s tím rozdílem, že zatímco tekoucí voda uděluje všem tělesům v daném místě konstantní rychlost, gravitace uděluje konstantní zrychlení.
Pokud se vám nepozdává představa sama sebe sedící v klidu na židli a přesto zrychleného, nelamte si s tím hlavu. Minimálně budete alespoň určitě souhlasit, že z pohledu pozorovatele v padajícím výtahu zrychlení jste. A to je ten pohled, který budeme potřebovat pro naše další povídání. V následující podkapitole o silném principu ekvivalence se k tomu ještě vrátíme a trochu upřesníme. Zatím to můžeme brát jako zvláštní a zajímavý důsledek našich úvah o gravitaci.
Nyní se nám naskytla cesta, jak zkoumat gravitaci jako takovou. I když ji na rozdíl od elektrické síly nedokážeme odstínit, máme způsob, jak zdánlině zrušit její působení - přechodem do volně padající vztažné soustavy. Ta je totiž inerciální, takže v ní platí zákony speciální relativity. Vznikla nám tak ideální výchozí pozice, protože nyní můžeme stavět nové poznání na již známých základech. Než se ale pustíme do aplikace našeho nového zjištění, musíme překonat jeden důležitý problém, který jsme zatím zamlčeli.
Vraťme se k představě volně padajícího výtahu. Abychom ho mohli oprávněně označit za inerciální soustavu, musí všechna tělesa splňovat první Newtonův zákon. To, jak už víme, znamená, že pokud jsou vůči výtahu vypuštěna z klidu nebo vykonávají rovnoměrný přímočarý pohyb, musí to tak i zůstat. Prakticky je to realizováno díky tomu, že všem tělesům včetně výtahu způsobuje gravitace přibližně stejné zrychlení. A protože zrychlení je vektorová veličina, znamená to urychlovat nejen stejnou měrou, ale i stejným směrem. Ze vzorce \eqref{4.1} ale vidíme, že gravitační síla (a tím pádem i zrychlení, které nám uděluje) klesá se vzdáleností od středu planety a navíc vždy do toho středu míří (mluvíme o tzv. radiálním gravitačním poli, které je naznačeno na obrázku 4.6 vlevo). Gravitační zrychlení tak obecně rozhodně není všude stejné. Rychlý výpočet nám ale ukáže, že pro většinu situací v běžném životě si můžeme situaci výrazně zjednodušit. Porovnejme, jak se bude lišit gravitační zrychlení na povrchu Země a ve výšce \(100\:\text{m}\) nad povrchem. Abychom dokázali výsledek rozumně interpretovat, vypočítejme rovnou relativní změnu, tedy vydělenou původní hodnotou zrychlení: \begin{align*} &\frac{g(0\:\text{m})-g(100\:\text{m})}{g(0\:\text{m})}= \frac{\frac{GM_z}{R_z^2}-\frac{GM_z}{\left(R_z+100\:\text{m}\right)^2}}{\frac{GM_z}{R_z^2}}=\frac{\frac{1}{R_z^2}-\frac{1}{(R_z+100\:\text{m})^2}}{\frac{1}{R_z^2}}= \\ &=1-\frac{R_z^2}{(R_z+100\:\text{m})^2} =1-\frac{6378000^2}{6378100^2}= 0{,}0000314\doteq0{,}003\:\%. \end{align*} Vidíme, že na 100 metrech výškového rozdílu činí změna gravitačního zrychlení jen něco málo přes tři tisíciny procenta, což je hodnota měřitelná jen s velmi kvalitním technickým vybavením, s běžně dostupnými měřidli bychom ji nenaměřili. Jako cvičení si můžete zkusit odvodit, v jaké nadmořské výšce se velikost gravitačního zrychlení změní alespoň o 1 % oproti povrchu.
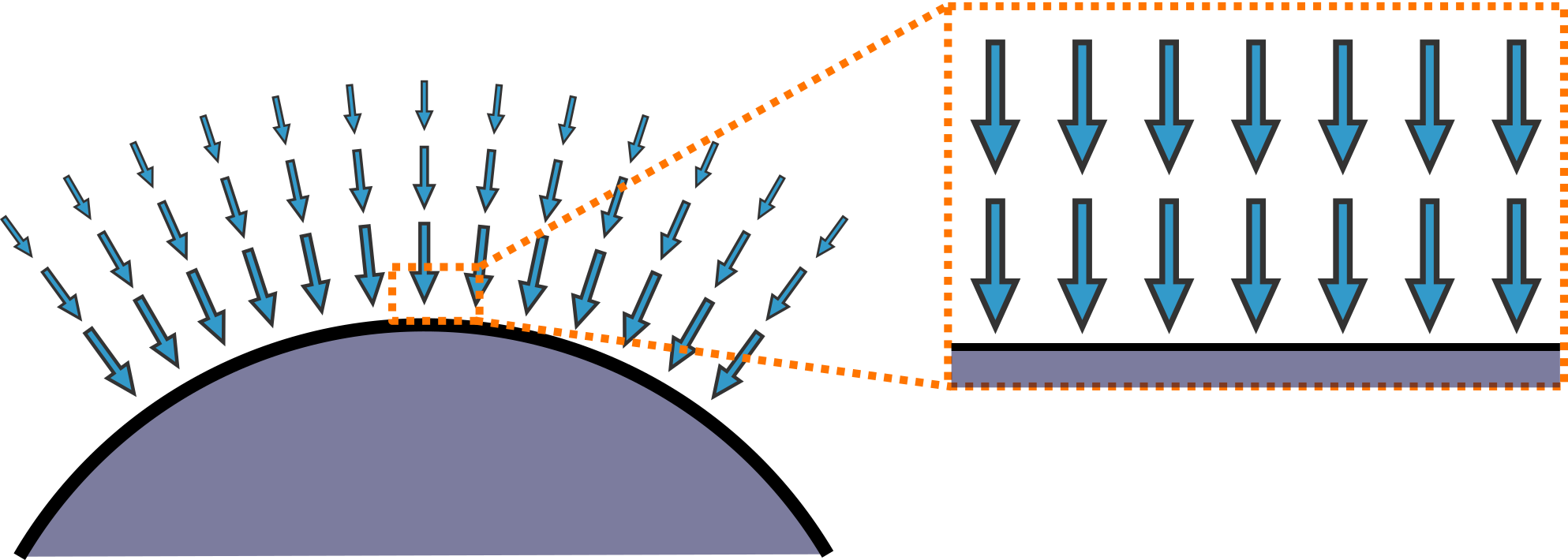
Obrázek 4.6 Gravitační pole kolem kulové planety má směr vždy do středu (radiální) a zmenšuje se se vzdáleností od povrchu. V měřítkách výrazně menších než jsou rozměry planety, můžeme s dostatečnou přesností považovat gravitační pole za homogenní, tedy mající všude stejný směr a velikost.
Je snadné si rozmyslet, proč je tato změna tak malá. Naše planeta je obrovská v porovnání s běžnými rozměrovými škálami lidského života. \(100\) metrů nebo i kilometr je zanedbatelná vzdálenost vůči poloměru Země. Stejně tak to dopadne i se směrem gravitačního zrychlení. Pokud bychom nechali volným pádem padat tělesa u nás a třeba na Novém Zélandu, obě tělesa budou urychlována směrem do středu Země, rozhodně tedy ne stejným směrem. Jakmile ale obě tělesa přiblížíme dostatečně blízko sebe, budou padat prakticky rovnoběžně (i když teoreticky vždy nějaký úhel jejich dráhy samozřejmě svírají). Opět zkusme rychlý výpočet. Dejme tomu, že v našem uspořádání nedokážeme měřit úhel menší než je jedna úhlová sekunda (tj. 1/3600 úhlového stupně, což je úhel, na jehož změření už potřebujeme poměrně drahá měřidla). Jak daleko od sebe bychom v zanedbatelné výšce nad zemí museli vypustit z klidu dvě tělesa, aby odchylka jejich pádů byla menší než přesnost našeho měření?
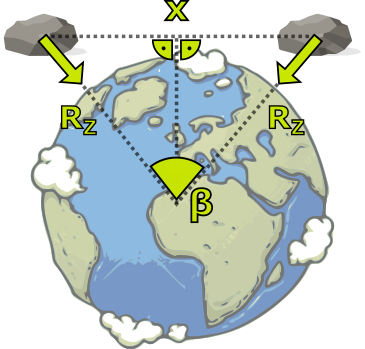
Obrázek 4.7 Nákres k výpočtu takové vzdálenosti dvou padajících předmětů na povrchu Země, abychom jejich pády považovali za rovnoběžné.
V pravoúhlém trojúhelníku na obrázku 4.7 vidíme, že platí \begin{equation*} \sin{\frac{\beta}{2}}=\frac{\frac{x}{2}}{R_z}=\frac{x}{2R_z} \Rightarrow x=2R_z\sin{\frac{\beta}{2}}. \end{equation*} Dosadíme-li za úhel \(\beta\) naši hraniční podmínku jedné úhlové sekundy, dostáváme vzdálenost těles přibližně 31 metrů. Pokud bychom hypoteticky nedokázali naměřit úhel menší než jeden stupeň (což už samo o sobě není v běžných podmínkách jednoduché), možná vzdálenost těles vzroste na 111 kilometrů! Vidíme tedy, že pokud se omezíme na dostatečně malou oblast, můžeme považovat gravitační pole Země za homogenní, tzn. mající všude v dané oblasti stejný směr a stejnou velikost.
Shrňme nyní naše úvahy. Abychom mohli zkoumat gravitaci relativisticky, potřebujeme vyjít z nějakého známého startovacího bodu. Tím jsou inerciální vztažné soustavy, protože v nich platí poznatky speciální teorie relativity. Problém spočívá v tom, že ty za přítomnosti gravitace nejsme schopni realizovat. Respektive, nejsme schopni je realizovat globálně, což zde prakticky znamená neomezeně velké. Jak jsme si ale už rozmysleli, lokálně (tj. v dostatečně malém měřítku) nám to projde. Naše soustava musí být dostatečně malá, aby se neprojevil nehomogenní charakter gravitace, a zároveň musí být vztažena k volně padajícímu tělesu (zkráceně řečeno, celá soustava musí volně padat). Technicky hovoříme o tzv. lokální inerciální soustavě, zkráceně LISu. Jak přesně malá musí tato soustava být? To záleží na konkrétní situaci. Třeba někde na oběžné dráze geostacionárních družic, kde je gravitační působení o něco slabší než na povrchu planety, nebude rozdíl oproti homogennímu poli tolik patrný, takže si můžeme dovolit uvažovat ve větších měřítkách. Obecně řekněme, že naše LIS musí být dostatečně malá na to, aby jakékoli odchylky od homogenní situace byly pod naše rozlišovací schopnosti. K tomu ale zároveň musíme dodat, že naše případné úvahy či experimenty se budou muset omezit nejenom na dostatečně malé vzdálenosti, nesmí ani příliš dlouho trvat. Pokud bychom totiž například nechali dvě tělesa z obrázku 4.7 padat dostatečně dlouho, je jen otázkou času, než jejich zanedbatelné, ale přesto nenulové vzájemné přibližování vzroste na měřitelnou úroveň, anebo prostě jen nedopadnou na zem. LIS tedy nebude lokální jen v prostoru, ale i v čase – takže vlastně v prostoročase.
Silný princip ekvivalence
Naše úvahy shrnuje (a dále rozšiřuje) tzv. silný princip ekvivalence, který (podle [5]) říká, že
V každém bodě prostoročasu existuje lokální inerciální systém, v němž platí stejné zákony jako ve speciální teorii relativity.
Již jsme si rozmysleli, jak volný pád naší soustavy pro nás dokáže gravitaci zdánlivě odstínit (a slovem zdánlivě zde myslíme uvnitř volně padající soustavy). Celý proces můžeme ale také obrátit. Ukažme si nyní, jak rovnoměrně zrychleným pohybem můžeme simulovat gravitaci.
Abychom se vyhnuli potížím s třením vzduchu, přenesme nyní náš pomyslný výtah do prázdného prostoru vesmíru, dostatečně daleko od gravitujících těles, a připevněme k němu motory (čímž z něj prakticky uděláme raketu). Ze začátku nechme motory vypnuté. Jak bude vypadat situace uvnitř? To už dobře známe. S vypnutými motory a dostatečně daleko od jakýchkoli jiných vnějších vlivů včetně gravitace je výtah inerciální soustavou, takže se vše vznáší ve stavu beztíže. Nyní nechme motory působit konstantní silou. Z druhého Newtonova zákona okamžitě plyne, že se raketa začne pohybovat s konstantním zrychlením \(\vec{a}\). Jak bude vypadat situace uvnitř rakety teď? Stačí si uvědomit, že z rakety se rázem stává neinerciální soustava, takže na všechna tělesa uvnitř bude z pohledu posádky rakety působit setrvačná síla působící proti směru pohybu. Cokoli není připoutané, je rázem tlačeno z pohledu letu rakety dozadu (samozřejmě při pohledu z venku je nám jasné, že předměty vlastně zaostávají za zrychlující raketou) se setrvačným zrychlením \(\vec{a_\text{s}}\), které je stejně velké, ale opačné než \(\vec{a}\). Zkuste se nyní vžít do situace astronauta v raketě v okamžiku zapnutí motorů, které budou raketě udělovat konkrétní hodnotu zrychlení \(9{,}8\:\text{m}\cdot\text{s}^{-2}\). Nejdříve si beztížně poletujete kabinou a najednou začne zadní stěna rakety zrychlovat směrem k vám a velmi rychle do vás narazí. Od stěny se ale neodrazíte, jste na ni přitisknuti, protože do vás neustále tlačí díky svému velkému zrychlení. Doslova vás hrne před sebou a kolem na stěnu dopadá vše, co ještě před chvilkou také volně plulo kabinou. Počkat… dopadá? Pokusíte se zvednout hlavu a zjistíte, že to jde. Pak se vzepřete na rukou. Není to tak těžké, do stěny vás sice tlačí setrvačná síla, ale vaše tělo je dokonale uzpůsobeno odolávat přítlačné síle. Dělá to celý váš život. Tedy aspoň dělalo do té doby, než jste se vydali mimo naši planetu a její gravitaci. Postavit se na nohy také není žádný problém. Rozhlédnete se kolem a uvědomíte si, že stojíte na zadní stěně rakety. Nebo lépe řečeno, zadní stěna rakety je nyní podlahou. Vezmete do ruky nejbližší předmět a pustíte ho. Spadne vám k nohám jak přitahován gravitací. Cítíte starý známý pocit, že takhle to má být, nohy dole, hlava nahoře.
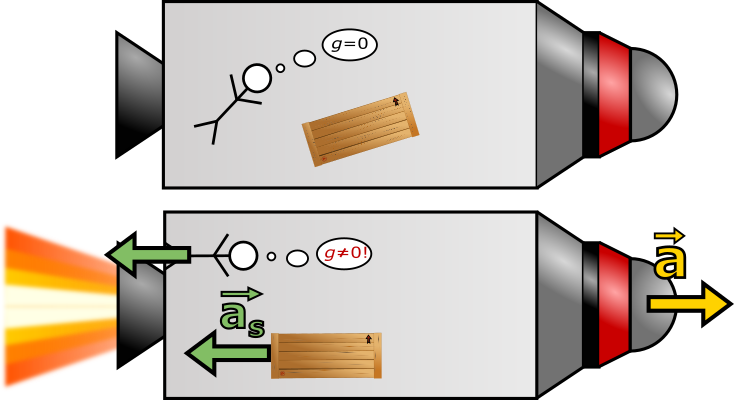
Obrázek 4.8 Nahoře: Pokud má raketa vypnuté motory, posádka uvnitř zažívá stav beztíže. Dole: Jakmile zapneme motory, začne na všechna tělesa uvnitř rakety působit setrvačné zrychlení proti směru pohybu. Toto zrychlení působí na všechna tělesa stejně. V malé raketě tak prakticky dokonale simuluje gravitační působení. Zadní strana rakety se rázem stává podlahou. Velikost tohoto jakoby gravitačního působení můžeme navíc velmi jednoduše nastavit zrychlením rakety.
I když co je to vlastně dole? Když Čech a Australan každý doma ukáží směrem dolů, rozhodně nebudou ukazovat stejným směrem. Ne nadarmo se obyvatelům nejmenšího světadílu říká protinožci. Dolů je pro nás vždy prakticky do středu Země - tam, kam směřuje gravitace. Ve zrychlující raketě je dolů ve směru působící síly, tedy směrem k motorům. Podobnost působící síly s gravitací je natolik blízká, že se rozhodneme ji otestovat. Zjistíme, že věci padají s konstantním zrychlením nezávisle na jejich tvaru či materiálu (samozřejmě nám to opět komplikuje tření vzduchu v kabině, ale to se dá obejít navlečením skafandru a následným vyčerpáním vzduchu). Vyskočíme směrem vzhůru a rázem dopadáme zpět (i když víme, že ve skutečnosti nás zrychlující podlaha opět dohnala, iluze je prakticky dokonalá). Můžeme zkusit libovolný pokus: stoupnout si na váhu, pracovat s pružinami, kyvadly, volným pádem těles, cokoli vás napadne. Vše probíhá stejně, jako bychom stáli na povrchu planety. Docházíme k jednoznačnému závěru. Pokud by nás někdo omráčil a my bychom se probudili uvnitř zrychlující rakety bez možnosti podívat se ven z okna na nějaký referenční bod, nedokázali bychom žádným pokusem ověřit, jestli raketa zrychluje anebo stojíme v gravitačním poli.
Pozorný čtenář by teď jistě mohl namítnout, že přece jen jedna možnost existuje. Již jsme si rozmysleli, že na naší planetě sice typicky předpokládáme, že tíhové zrychlení má v dané situaci všude stejnou velikost a směr (schválně, jak že takovému typu pole říkáme?), ale to je jen přiblížení dané malými rozměry naší situace v porovnání s celou planetou. Pokud bychom svá měření provedli dostatečně velká, skutečný sférický charakter gravitace by se projevil. Na druhou stranu v přímočaře zrychlující vesmírné lodi jsou směr i velikost setrvačného zrychlení doopravdy všude stejné. Pokud by tedy byla naše loď dostatečně veliká a naše měření dostatečně přesné, rozdíl by se najít dal. To znamená, že chceme-li, aby iluze byla dokonalá, musíme se zabývat dostatečně malou situací.
Z našich úvah tedy plyne další možná formulace silného principu ekvivalence (opět podle [5]):
Gravitační pole je lokálně ekvivalentní zrychlenému systému.
Slovo lokální zde používáme stále ve stejném významu – na dostatečně malém prostoru a po dostatečně krátkou dobu (argument je zde stejný jako u zavedení lokální inerciální soustavy výše). Pokud se vám nelíbilo tvrzení v poznámce 4.3, že i když stojíme v klidu na zemi, jsme ve skutečnosti zrychlení, silný princip ekvivalence může pomoci. Podle něj není třeba přímo tvrdit, že se pohybuje se zrychlením (i když vůči libovolnému blízkému LISu to je pravda), stačí mít na paměti, že cítit účinky gravitace je fyzikálně ekvivalentní se zrychlením pohybem bez gravitace. Naše prožitky či lépe řečeno naše pozorování i experimenty, které provádíme, vše dopadne stejně, jako bychom zrychlovali. Nemusíme tvrdit, že je to přesně to samé, stačí, že je to efektivně to samé.
Možná vás už napadlo, že se nám tak nabízí možnost, jak simulovat pozemskou gravitaci na meziplanetárních letech. Stačilo by mít neustále zapnuté motory, aby loď zrychlovala se zrychlením \(9{,}8\:\text{m}\cdot\text{s}^{-2}\). Posádka si tak možná bude připadat trochu jako ve výtahu jedoucím vzhůru, protože cíl bude „nad jejich hlavami“, ale na tom není nic špatného. Ve vesmíru si můžeme vybrat, kde je „nahoře“. A aby pak dokázali u cíle zastavit, mohla by se loď v polovině cesty otočit o 180° a začít se stejným zrychlením brzdit. „Gravitace“ bude fungovat stále, akorát tentokrát bude k cíli směřovat podlaha a posádka pojede „výtahem“ dolů. Bohužel se nám do této krásné teoretické představy promítají praktické komplikace a to zejména náročnost této metody na spotřebu paliva. Výhoda vesmírného cestování spočívá v tom, že po dosažení určité rychlosti můžeme vypnout motory a díky absenci odporu prostředí si „zadarmo“ plout vesmírem konstantní rychlostí (na Zemi naopak musíme neustále překonávat odpor prostředí, takže chceme-li se v jakémkoli dopravním prostředku pohybovat konstantní rychlostí, musíme alespoň trochu neustále „šlapat na plyn“). Zatím se tedy zdá být nereálné, aby si s sebou raketa mohla vzít na (prakticky jakkoli dlouhou) cestu dostatek paliva na to, aby celou dobu zrychlovala. Naštěstí existuje jednodušší řešení, namísto zrychlování a zpomalování můžeme celou raketu roztočit podél směru letu a toto otáčení raketě po celou dobu letu zůstane. Gravitaci tak bude simulovat odstředivá síla, což je řešení, které jste už určitě viděli v nějakém vědecko-fantastickém filmu. I v tomto případě je třeba překonat určité praktické komplikace, ty jsou už ale nad rámec našeho povídání.
Mimochodem, nyní jsme se v našich úvahách vrátili kruhem zpět na začátek této kapitoly. Je-li obecná teorie relativity důsledkem snahy rozšířit relativistickou fyziku na libovolné neinerciální soustavy a zároveň jsme si rozmysleli, že lokálně je zrychlení naší soustavy nerozlišitelné od gravitačního působení, dostáváme se k závěru, že obecná relativita je také (ale vlastně zejména) teorií gravitace.
Traduje se, že Einstein sám při svých úvahách v tomto bodě nevěděl, jak pokračovat, a byl to jeho spolužák, přítel a později kolega, matematik Marcel Grossman, kdo Einsteina upozornil na podobnost důsledků principu ekvivalence a vztahů v diferenciální geometrii. Ta se zabývá zejména popisem geometrie na zakřivených plochách a v zakřivených prostorech (více se o tom zmíníme později). První vědecké články popisující základy OTR napsal Einstein právě ve spolupráci s Grossmanem a formuluje je zde právě v geometrickém pojetí. Abychom ale dokázali toto překvapivé spojení gravitace a geometrie pochopit, musíme nejdříve udělat, stejně jako je tomu asi v každé učebnici obecné relativity, geometrickou odbočku. Pokusíme se rozebrat hlavní myšlenky diferenciální geometrie, abychom pak ve finále dokázali pochopit již zmíněnou základní tezi OTR, kterou běžně nacházíme v populárních knihách: Gravitace je zakřivení prostoročasu.
Shrnutí kapitoly 4.1
Obecná teorie relativity (OTR) je relativistická teorie gravitace. Mimo jiné zobecňuje speciální teorii relativity pro případy, kdy nemůžeme vliv gravitace zanedbat.
Jedním z výchozích principů OTR je princip ekvivalence, který má několik verzí. Nejjednodušší z nich, tzv. slabý princip ekvivalence, říká, že všechna tělesa padají v daném místě se stejným zrychlením. Tato skutečnost je experimentálně ověřována s vysokou přesností, newtonovské teorie gravitace ji ale nijak nevysvětluje.
V přítomnosti gravitace nemůžeme realizovat globální inerciální systém, tak jako v STR, protože nemáme volné částice v pravém slova smyslu. Díky tomu, že gravitace působí na všechny předměty a částice stejně, můžeme ale zavést volně padající lokální inerciální systémy (LIS), ve kterých jsou účinky gravitace lokálně odstraněny.
Slabý princip ekvivalence lze zobecnit na tvrzení, že zrychlená soustava v místech bez gravitačního pole je lokálně ekvivalentní soustavě, v níž působí gravitace - tomu říkáme silný princip ekvivalence. Z toho také plyne, že v lokálních inerciálních systémech nejen pohyb těles, ale všechny fyzikální děje probíhají stejně, jako v STR. Díky tomu dokážeme řadu poznatků o vlivu gravitace na fyzikální děje odvodit z již známých zákonů STR.
Důsledkem těchto úvah je přístup, kdy se na pád tělesa v gravitačním poli díváme ne jako na pohyb způsobený gravitační silou (jak to říká newtonovská teorie), ale jako na nejpřirozenější pohyb vůbec (konec konců, vůči LISu se také těleso pohybuje rovnoměrně přímočaře). Síla, kterou cítíme, když stojíme na zemi, je v tomto pohledu důsledkem toho, že nám země brání pokračovat ve volném pádu.
Příklady ke kapitole 4.1
Gravitační vs. elektrická síla
Pomocí Newtonova a Coulombova zákona vypočítejte, kolikrát je elektrická síla mezi protonem a elektronem silnější než gravitační (potřebné fyzikální konstanty můžete dohledat na internetu).
Rozjíždějící se tramvaj
Když nastoupíme do zadní části tramvaje (nebo samozřejmě jakéhokoli jiného dostatečně prostorného dopravního prostředku), můžeme zcela normálně projít vnitřkem tramvaje dopředu. Pokud se ale v tu chvíli začne tramvaj rozjíždět, naše chůze kupředu se stane zjevně náročnější, jako bychom šli do mírného kopce, i když tramvaj je celou dobu v rovině. Vysvětlete tento jev. Jak souvisí s chůzí do kopce? (Nakreslete si při řešení obrázek mírné nakloněné roviny.) Vypočítejte úhel stoupání, který odpovídá situaci, kdy se tramvaj rozjíždí se zrychlením \(1\:\text{m}\cdot{s}^{-2}\).
Horní 1 %
Určete, v jaké nadmořské výšce se velikost gravitačního zrychlení změní alespoň o 1 % oproti povrchu.
Na kolotoči jako doma
Představme si, že jsme na vesmírné lodi, jejíž obytná část má tvar prstence s poloměrem zhruba \(50\:\text{m}\). Po většinu cesty se loď otáčí kolem své podélné osy, aby posádky v prstenci cítila standardní zemskou „gravitaci“ \(9{,{8\:\text{m}\cdot\text{s}^{-2}\). Jak dlouho musí trvat jedna otáčka, aby to byla pravda?
4.2 Geometrická odbočka
Co to znamená, že je prostoročas zakřivený? Tuto otázku se nyní budeme snažit zodpovědět, ale nebude to jen tak. Představit si prostoročas samotný je pro nás velmi obtížné, natož pak do situace vnášet další geometrii. Celou situaci si musíme nejdřív zjednodušit. Začneme tedy s něčím, co si nejen dokážeme představit, ale co je i blízké naší každodenní zkušenosti. Místo čtyř souřadnic, z nichž jedna je časová, se pro začátek omezíme jen na dvě prostorové. Podíváme se na zakřivené plochy.
Prakticky všechna geometrie, se kterou se člověk na základní a střední škole setká, se odehrává v rovině. V této, tzv. eukleidovské geometrii, založené na několika axiomech zformulovaných řeckým matematikem Eukleidem, platí mnoho nám tak dobře známých geometrických tvrzení jako například \begin{array} {l l} \tag{4.2}\label{4.2} \bullet & \text{Nejkratší spojnice dvou bodů je úsečka (tj. část přímky).} \\ \bullet & \text{Součet všech vnitřních úhlů v trojúhelníku je }180^°\text{.} \\ \bullet & \text{Rovnoběžky se nikdy neprotnou (respektive kolmá vzdálenost rovnoběžek je všude stejná).} \\ \bullet & \text{Mezi poloměrem kružnice }r\text{ a jejím obvodem }o\text{ platí vztah }o=2\pi{}r\text{.} \\ \end{array} Funguje to i obráceně, pokud na libovolné ploše zjistíme platnost tvrzení výše, jedná se pravděpodobně o rovinu. Stejná tvrzení platí také v prostoru. Stačí si uvědomit, že v prostoru lze každým trojúhelníkem, dvojicí rovnoběžek, kružnicí nebo jen dvojicí bodů proložit rovinu (dvěma body lze dokonce proložit nekonečně mnoho rovin). Takovému prostoru pak také říkáme eukleidovský a čtenáři se může zdát překvapivé, že máme potřebu prostor nějak dál pojmenovat. Je to proto, že i když eukleidovská geometrie má pro náš život největší význam (například s její pomocí navrhujeme stavby, stroje apod.), existují i jiné geometrie, souhrnně jim říkáme neeukleidovské. Podívejme se nyní na několik návodných příkladů takových geometrií.
Povrch koule poprvé
Povrch koule neboli sféra je naší běžné zkušenosti velmi blízký. Snad každému se někdy, ať už dobrovolně či ne, dostal do ruky míč. Podívejme se nyní, jak na takové sféře dopadnou geometrické poučky \eqref{4.2}. Vřele doporučuji si všechny následující úvahy opravdu vyzkoušet vlastníma rukama. Nemáte-li po ruce míč či větší kouli, poslouží i nafukovací balónek. Nejedná se sice o přesnou kouli, ale, jak se ještě budeme zmiňovat, geometrie zde funguje stejně.
Pro začátek je nejlepší začít se spojnicí dvou bodů na povrchu. Již na první pohled je jasné, že to nemůže být úsečka, protože povedeme-li z jednoho bodu na sféře přímku, prakticky okamžitě sféru opustíme. To nám ale nebude dovoleno, protože bychom pak už vlastně nezkoumali povrch sféry. Jak tedy takové dva body spojit? Určitě by vás napadlo využít například provázek. Když ho natáhneme mezi dva body, můžeme nejen odečíst délku nejkratší spojnice, ale vidíme i její tvar vytyčený provázkem. Ukazuje nám tím vlastně z podstaty věci nejpřímější cestu mezi dvěma body. Takovou, která nás vede nejkratší cestou k cíli, ani kousek stranou. Alternativou k provázku, je úzký proužek papíru. Ten je stejně jako provázek rovný, když ho položíme například na desku stolu, ale může se ohnout podle toho, jak vyžaduje zakřivení dané plochy. Vytváří tak vlastně zakřivený ekvivalent úsečky právě ve smyslu nejkratší spojnice dvou bodů.
Poznámka 4.4
Určitě vás v tuto chvíli napadne námitka, že samozřejmě nejkratší spojnicí dvou bodů je stále úsečka, jen tato úsečka prochází vnitřkem sféry. Naše stará známá geometrie stále funguje, jen musíme o celé situaci uvažovat prostorově a neomezovat se jen na povrch koule. To je ale přístup, který pro nás nebude dovolen. Je velmi lákavé a zároveň přirozené představit si sféru v běžném eukleidovském prostoru a dívat se na celou situaci „shora“, lépe řečeno z vyššího rozměru, protože (jak budeme ještě ukazovat), sféra je jakožto plocha dvourozměrný objekt, ale její zakřivení se nám nejlépe chápe a vizualizuje vnořeno v třírozměrném prostoru (mluvíme o tzv. vnější geometrii – čímž máme na mysli zakřivení dané plochy v prostoru). Jenže celá naše geometrická odbočka má jeden jasný účel. Co nejlépe pochopit, co to znamená zakřivení prostoročasu. Ten má čtyři rozměry (tzn. je popsán čtyřmi souřadnicemi), ale my nemáme žádnou možnost, teoretickou ani praktickou, jak se podívat do nějakého hypotetického pátého rozměru a z něj toto zakřivení zkoumat. Musíme tak činit zevnitř prostoročasu samotného. Jsme tedy v situaci analogické nějaké dvourozměrné bytosti žijící na dvourozměrné ploše. V popularizačních knihách se často mluví například o mravenci – bytosti sice trojrozměrné, ale maličké a nemohoucí podívat se na svůj svět z výšky. Chtě nechtě se tedy musí zabývat vnitřní geometrií, tedy geometrickými zákonitostmi uvnitř dané plochy. Koneckonců, odmyslíme-li si letadla a rakety, jsme v takové situaci i my lidé, zkoumající a žijící na obrovské (přibližně) sféře – naší planetě. Až do relativně nedávné doby jsme nedokázali vystoupat vysoko do nebe či až na oběžnou dráhu a prohlédnou si tvar naší planety. Přesto lidé v minulosti nepotřebovali létající stroje, aby správně poznali tvar Země. Vzpomeňme na Eratosthéna z Kyrény, který známým praktickým experimentem s měřením délek stínů a pomocí chytré geometrické úvahy nejen ukázal, že Země je kulatá, ale i s velmi dobrou přesností spočítal její obvod. Hezký popis a demonstraci Erathosthénova důkazu najdeme v podání známého popularizátora vědy Carla Sagana v seriálu Cosmos.
Video 4.9 Nejkratší spojnice dvou bodů na sféře je vždy část tzv. hlavní kružnice.
Dá se geometricky dokázat, že spojnice libovolných dvou různých bodů na sféře je vždy část tzv. hlavní kružnice (obrázek 4.9), tedy kružnice se středem ve středu koule a o stejném poloměru. Hezkou ilustrací celé situace je například glóbus. Pokud se pokusíme proužkem papíru spojit dvě místa o stejné zeměpisné délce, spojnice bude přímo část příslušného poledníku, protože poledníky jsou hlavní kružnice na glóbu. Zkuste na druhou stranu spojit dvě místa o stejné zeměpisné šířce. Pokusíte-li se místa spojit proužkem papíru po příslušné rovnoběžce dále od rovníku, nepodaří se vám papír plně přitisknout na plochu koule. Je to proto, že rovnoběžky (s výjimkou rovníku) nejsou hlavní kružnice na sféře, proto ani jejich části neodpovídají „úsečkám“ na sféře. My sice můžeme tato dvě místa spojit příslušnou rovnoběžkou, na glóbu jsou přece jasně nakresleny, ale jak nyní ukážeme, nejedná se o spojení „přímé“ a ani nejkratší.
Video 4.10 Půjdeme-li na sféře co „nejrovněji“, naší trajektorií bude opět hlavní kružnice.
Co to vlastně znamená jít na sféře přímo? V rovině nám tento pojem nedělá problém. Jdeme stále stejným směrem, nezatáčíme ani na jednu ani na druhou stranu a naše trajektorie se i podle toho jmenuje – přímka. Co by se stalo, kdybychom se snažili jít na sféře stále rovně? Rozhodně se nebudeme pohybovat po přímce, protože, jak už jsme zmiňovali, ta by nás vynesla ze sféry pryč. Přesto si dokážeme představit, jak by to dopadlo. Ať už pomocí kompasu, satelitní navigace, nebo prostě jen zablokováním volantu našeho vozidla, jistě je možné pohybovat se na Zemi pořád rovně (komplikaci v podobě terénních a jiných přírodních překážek jako propasti, hory a oceány ponechme nyní stranou). Na našem demonstračním míči k tomuto účelu poslouží velmi dobře právě proužek papíru, protože ten má na rozdíl od provázku tendenci být stále rovný (respektive snadno na něm poznáme, když není). Pokud na povrch koule přiložíme proužek papíru, jasně nám ukazuje, co to znamená jít rovně v dané situaci. S dostatečně dlouhým papírkem bychom mohli ukázat, že analogií přímky na povrchu koule je opět hlavní kružnice. Půjdeme-li tedy na kouli dostatečně dlouho rovně, dostaneme se zpět do výchozího bodu (video 4.10). Ačkoli se snažíme jít neustále rovně, zakřivení povrchu koule způsobí, že naše trajektorie není část přímky.
Zkusíme-li s pomocí naší papírkové metody vyrazit ve směru zeměpisné rovnoběžky (s výjimkou rovníku), záhy zjistíme, že přiložený papírek z ní uhýbá. Na sféře totiž není možné jít neustále "rovně" a přitom zůstat na stejné zeměpisné šířce. Rovnoběžky (s výjimkou rovníku) nejsou nejpřímější spojnice bodů a spojit dva body na sféře rovnoběžkou je jako spojit dva body v rovině křivkou namísto úsečky.
Podobně můžeme ukázat, že spojení dvou míst rovnoběžkou není nejkratší možné (ač se tak může na první pohled zdát). Toto tvrzení lze dokázat obecně, ale my zůstaneme u praktického příkladu. Zapněte si v prohlížeči mapy, které obsahují letadlová spojení, např. Google Maps. Zadejte leteckou cestu mezi dvěma vzdálenými městy na zhruba stejné zeměpisné šířce, například z New Yorku do Madridu (zde činí rozdíl v zem. šířce zhruba pouhých půl stupně – obrázek 4.11). Všimněte si tvaru zobrazené trajektorie letu. Nesleduje příslušnou rovnoběžku, ale je zobrazena jako oblouk. Ačkoli je jeho tvar jistě zkreslený zobrazením na ploché mapě, jistě vám připomíná již zmíněné části hlavní kružnice. Aerolinky určitě nebudou jen tak ztrácet čas a peníze za zbytečně dlouhé lety, je v jejich zájmu dostat se do cíle po co nejkratší dráze (samozřejmě musí pracovat také s dalšími vlivy jako je počasí, vzdušné proudění apod., ale to je to opět jen komplikace navíc). Zdá se tedy, že spojení dvou míst po rovnoběžce opravdu není nejkratší. Na mapě si můžete takto zkusit spojit i jiná místa. Čím budou dále od sebe, tím bude rozdíl výraznější. Mimochodem, může vám připadat, že zde úvahami o létání porušujeme naši úmluvu, že se budeme striktně držet povrchu. Není zde ale nic, co by naši domluvu narušovalo. Letu využíváme pouze ke zdolání přírodních překážek (v tomto případě Atlantického oceánu), nijak zde nepracujeme s další dimenzí. Můžeme si představit, že letadlo by teoreticky mohlo letět po celou dobu těsně nad povrchem. Případně, kdyby se dalo mezi oběma městy cestovat suchou nohou, platily by naše úvahy stejně například pro cestu autem. Názorně si také můžete situaci vyzkoušet v appletu.
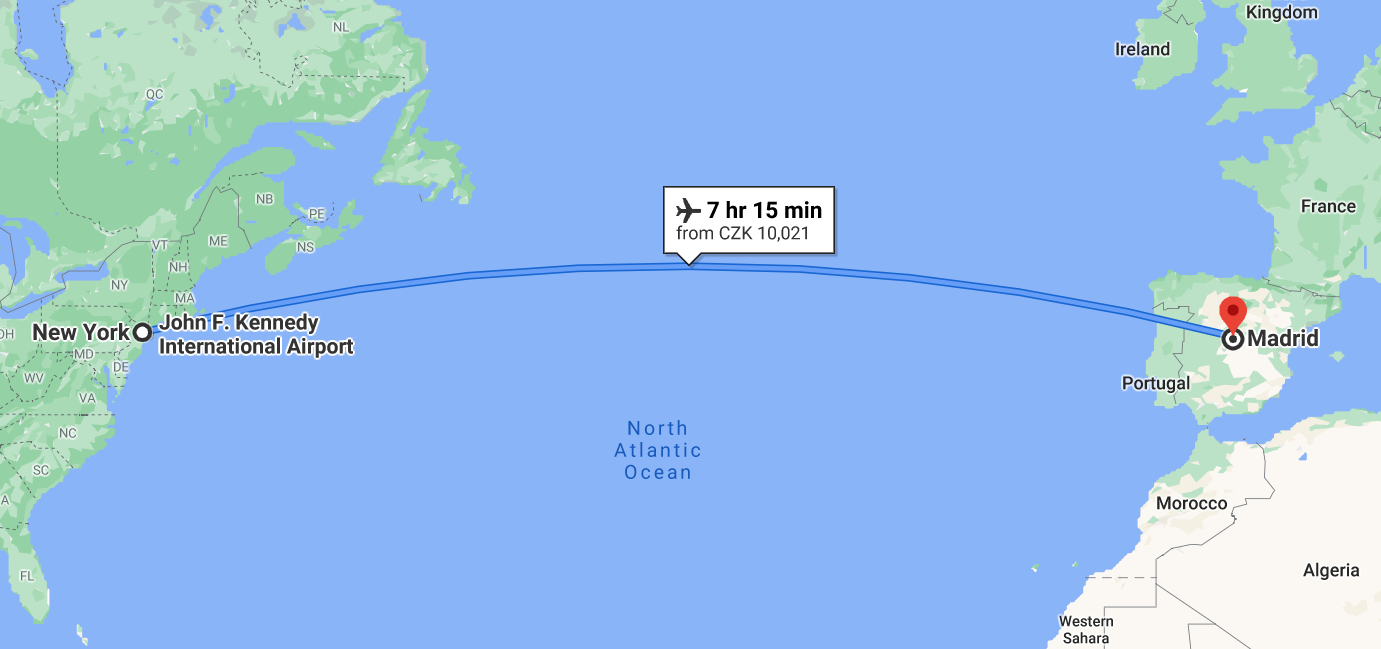
Obrázek 4.11 Cesta letadlem z New Yorku do Madridu (jejichž zeměpisná šířka je velmi podobná) pomocí Google Maps. Vidíme, že naznačená cesta na mapě nesleduje zdánlivě nejpřímější spojnici (po zeměpisné rovnoběžce), ale odpovídá části hlavní kružnice.
Při našich úvahách jsme na sféře objevili zakřivené analogie dvou pojmů známých z rovinné geometrie, úsečky a jejím pomyslným protažením i přímky. Podobné analogie se jistě dají provést i pro jiné zakřivené plochy, i když třeba nebudou tak dobře představitelné jako u sféry. Zobecnění přímky, jakožto trajektorie tělesa, která jde stále „rovně“, se říká geodetika, a jedná se o velmi důležitý pojem nejen v geometrii, ale i v obecné teorii relativity. Proto s ní budeme i my dále hodně pracovat. Podobně jako v rovině je úsečka, tj. část přímky o konečné délce, nejkratší spojnice dvou bodů, je i na zakřivené ploše část geodetiky touto nejkratší spojnicí. Z principu věci je asi jasné, že tvar geodetiky je dán zejména geometrií dané zakřivené plochy (už víme, že v případě koule se jedná vždy o některou z hlavních kružnic) a u obecně komplikovaně zakřivených ploch se mohou geodetiky i v různých částech plochy svým tvarem lišit.
Vraťme se nyní o krok zpět. Začali jsme uvedením několika vybraných geometrických tvrzení \eqref{4.2} platných v eukleidovské geometrii. Už jsme si rozmysleli, jak dopadá první z těchto tvrzení. Nejkratší spojnice dvou bodů na sféře není úsečka, ale část hlavní kružnice. Podívejme se nyní i na zbývající tvrzení.
Chceme-li zkoumat součet vnitřních úhlů v trojúhelníku, musíme nejdříve vyřešit malý problém. Jak vypadá trojúhelník na sféře? Jak ho narýsovat? Inspirujme se v rovině. Tam vznikne trojúhelník spojením třech různých bodů úsečkami. Jelikož ekvivalentem úsečky na sféře je část hlavní kružnice, nabízí se přirozeně trojúhelník vytvořit pomocí spojnic jednotlivých bodů (video 4.12 vlevo). Zkuste si takový trojúhelník vytvořit na svém modelu sféry. Pomůckou vám mohou být fixy, proužky papíru nebo pružné pravítko. Následně můžete zkusit změřit vnitřní úhly úhloměrem. Jsme sice zvyklí měřit úhly mezi přímkami, nicméně úhel mezi dvěma protínajícími se kružnicemi můžeme definovat jako úhel mezi jejich příslušnými tečnami v daném bodě. Pokud je navíc naše koule dostatečně velká (či úhloměr dostatečně malý), stačí úhloměr přiložit k danému vrcholu a změřit úhel jako bychom byli v rovině, protože na malém okolí vrcholu trojúhelníku se kružnice a tečna příliš neliší. Anebo ani nutně přesně měřit nemusíme. Stačí najít takový trojúhelník, kde je velikost vnitřních úhlů zjevná. Dokážete takový příklad najít?
Představíme-li si sféru opět jako glóbus, můžeme sestrojit trojúhelník, který tvoří části rovníku a dvou poledníků. Z definice jsou poledníky vždy kolmé na rovník, takže automaticky máme v trojúhelníku dva devadesátistupňové vnitřní úhly. Poledníky se protínají na severním či jižním pólu pod nějakým nenulovým úhlem (podle toho jaké poledníky zvolíme), takže dostáváme trojúhelník, jehož součet vnitřních úhlů je větší než \(180^°\). Speciálně můžeme například najít takové dva poledníky, které jsou na sebe na pólech kolmé, takže dostáváme součet vnitřních úhlů \(270^°\) (jako na obrázku 4.12 vpravo). Obecně vzato, pokud budete dále zkoušet jakékoli jiné trojúhelníky, všechny budou mít součet vnitřních úhlů větší než \(180^°\). Nejde to jinak. Je to přímý důsledek geometrie na sféře.

|
Video 4.12 Vlevo: Obecný trojúhelník na sféře vytvořený nejkratšími spojnicemi třech různých bodů.
Vpravo: Ukázka trojúhelníku na sféře se součtem vnitřních úhlů 270°.
Video 4.13 Dvě původně rovnoběžné trajektorie se na sféře protnou.
Další geometrické tvrzení mluvilo o rovnoběžkách, a tentokrát nikoli zeměpisných rovnoběžkách. Ty získali svůj název díky tomu, že se skutečně jedná o rovnoběžné křivky v běžném smyslu, protože se nikdy neprotnou a neustále od sebe zůstávají na stejnou vzdálenost. Ty ale uvažovat nebudeme, protože už víme, že se nejedná o přirozený ekvivalent rovnoběžných přímek. Těmi jsou hlavní kružnice. Ty z principu nemohou být nikdy rovnoběžné ve smyslu konstantní kolmé vzdálenosti, protože pak by nebyly obě hlavními kružnicemi. Když si ale tyto kružnice opět představíme jako trajektorie nezahýbajícího tělesa, můžeme se podívat, jak dopadne situace, kdy vyšleme dvě tělesa rovnoběžnými směry. V rovině by v takové situaci tělesa začala vykreslovat rovnoběžky. Na sféře se můžeme například postavit na rovník a obě tělesa v nějaké vzdálenosti od sebe vyslat na sever (nebo alternativně na jih). Poledníky, po kterých se budou tělesa pohybovat, jsou oba kolmé na rovník, takže minimálně zpočátku to opravdu vypadá, že tělesa vysíláme stejným směrem. Snadno ale vidíme, že poledníky se k sobě nejenom přibližují, ale dokonce protínají na pólu. Podobný výsledek bychom dostali, kdybychom vyslali tělesa na kouli libovolným směrem (video 4.13). Na kouli se tedy původně rovnoběžné trajektorie k sobě přibližují, až se nakonec protnou. Znovu dostáváme výsledek velmi odlišný od geometrie v rovině.
Posledním ze zmíněných tvrzení byl vztah mezi poloměrem kružnice a jejím obvodem, \(o=2\pi{}r\). Často tento vztah chápeme jako definici čísla pí, ve škole je to poprvé, kde se s ním setkáváme (sice častěji v souvislosti s průměrem kružnice \(o=\pi{}d\), ale fakticky se jedná o stejný vztah). Prakticky nám říká, že obvod kružnice je přímo úměrný jejímu poloměru. Kružnice, která má dvojnásobný poloměr než jiná, bude mít i dvojnásobný obvod. Na sféře to dopadne ale jinak. Vyjdeme-li z definice kružnice jako množiny bodů, které jsou od zvoleného středu stejně daleko, máme praktický způsob, jak na sféře kružnici zkonstruovat. Na obrázku 4.14 vlevo vidíme, že pro každou kružnici je její „poloměr“ \(r\) měřený na sféře větší, než příslušný eukleidovský poloměr \(r^\prime\) ležící uvnitř koule, když si ji představujeme jako objekt v třírozměrném prostoru. Nutně tedy musí platit, že \(o\lt{}2\pi{}r\) a to pro libovolnou kružnici na sféře. Pokud jde o přímý matematický vztah mezi obvodem kružnice a jejím sférickým poloměrem, můžeme relativně snadno odvodit, že na sféře o poloměru \(R\) platí \begin{equation*}\label{4.3}\tag{4.3} o=2\pi{}r^\prime=2\pi{}R\sin{\frac{r}{R}}\lt{}2\pi{}r. \end{equation*}
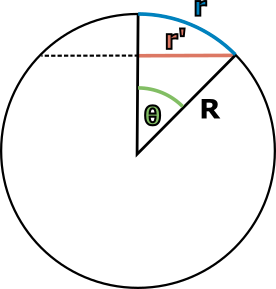
Vztah mezi obvodem kružnice na sféře a jejím naměřeným sférickým „poloměrem“ \(r\), tedy vzdáleností všech bodů kružnice od středu měřenou na ploše sféry o poloměru \(R\), vidíme na obrázku, kde je situace pro větší přehlednost nakreslena z boku. Zvolená kružnice se středem „na severním pólu“ je čárkovaně. Ačkoli se dovnitř sféry nedostane, můžeme si představit vnitřek sféry jako běžný eukleidovský prostor, kde se nachází také příslušný eukleidovský poloměr \(r^\prime\) kružnice. Platí tedy nutně \(o=2\pi{}r^\prime\). Nyní stačí najít vztah mezi \(r\) a \(r^\prime\). Oblouk délky \(r\) vytyčuje vůči středu koule úhel \(\theta\) a platí \(r=\theta{}R\) (pozor, jak si budeme ještě ukazovat, tento vztah funguje jen tehdy, když je úhel \(\theta\) v radiánech, ne ve stupních). Dále z pravoúhlého trojúhelníku na obrázku vidíme, že platí \(\sin{θ}=r^\prime/R\). Dáme-li všechny tyto vzorce dohromady, dostáváme
\begin{equation*} o=2\pi{}r^\prime=2\pi{}R\sin{\theta}=2\pi{}R\sin{\frac{r}{R}}. \end{equation*}
Obrázek 4.14 Vlevo: Dvě kružnice na sféře o různých poloměrech a jejich příslušné „eukleidovské“ poloměry uvnitř sféry. Jelikož pro každou kružnici platí \(r>r^\prime\), je i nutně \(2\pi{}r\gt{}o\).
Vpravo: Graf závislosti \eqref{4.3} pro \(R = 1\:\text{m}\) – modře, v porovnání s lineární závislostí \(o=2\pi{}r\) platící v rovině - červeně. Všimněme si dvou detailů. Za prvé, obvod kružnice na sféře s rostoucím poloměrem stoupá až do maximální možné hodnoty \(2\pi{}R\) (což je v tomto případě přibližně \(6{,}28\:\text{m}\)) a opět klesá podle očekávání. Za druhé, pro malé poloměry jsou obě závislosti prakticky nerozeznatelné. To znamená, že pokud bychom chtěli pomocí konstrukce kružnic testovat, zda se nacházíme na rovině či na sféře, museli bychom zkonstruovat kružnice dostatečně velké v porovnání s poloměrem sféry. Zkuste si sami ověřit, že aby byl rozdíl mezi modrou a červenou závislostí alespoň \(1\:\%\), museli bychom v případě planety Země vytvořit kružnici o poloměru zhruba \(1500\:\text{km}\), což měřeno od severního pólu na jih odpovídá posunutí v zeměpisné šířce o cca \(15^°\). Pro srovnání, rozdíl v zeměpisné šířce mezi severním pólem a severním polárním kruhem je zhruba \(23{,}5^°\).
Shrňme si nyní, jak dopadla naše vybraná geometrická tvrzení na sféře: \begin{array} {l l} \tag{4.4}\label{4.4} \bullet & \text{Nejkratší spojnice dvou bodů je oblouk (část hlavní kružnice).} \\ \bullet & \text{Součet všech vnitřních úhlů v trojúhelníku je větší než }180^°\text{.} \\ \bullet & \text{Původně rovnoběžné „přímky“ na sféře se k sobě přibližují a dříve nebo později se protnou.} \\ \bullet & \text{Mezi poloměrem kružnice }r\text{ a jejím obvodem }o\text{ platí vztah }o\lt{}2\pi{}r\text{.} \\ \end{array} Platnost všech tvrzení si můžete vyzkoušet v appletu (z něhož jsou pořízena videa v této podkapitole).
Další geometrie
Na geometrii sféry se ještě detailněji podíváme později, před tím si pojďme ukázat další příklady. Ukazuje se, že existuje celá řada zakřivených ploch, kde kvalitativní geometrická tvrzení \eqref{4.4} dopadnou stejně. Příkladem je třeba elipsoid. A není se zas tak čemu divit, protože ten vznikne „natažením“ či "splácnutím" koule do různých směrů (obrázek 4.15 vlevo). Nebo opačně, koule je vlastně speciálním případem elipsoidu, který má stejnou šířku, délku i hloubku. Pokud jste si v předchozí podkapitole zkoušeli sférickou geometrii na balónku, prakticky jste pracovali s objektem bližším elipsoidu než kouli. Dalším příkladem nyní už neuzavřené plochy je eliptický paraboloid (obrázek 4.15 vpravo). Jedná se o plochu, kterou když orientujeme jako zde na obrázku a rozřízneme ji ve svislém směru, dostaneme vždy parabolu. Pokud ji rozřízneme vodorovně, dostáváme vždy elipsu (či v případě rotačně symetrického paraboloidu kružnici – tento případ je i na obrázku). S malým výřezem paraboloidu se můžeme nejčastěji setkat u parabolických antén na domech (nesprávně se jim často říká satelit).
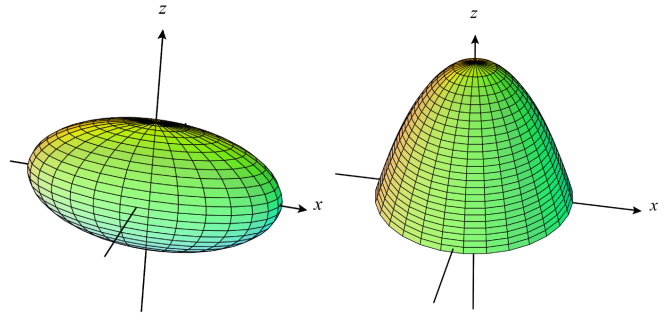
Obrázek 4.15 Vizualizace elipsoidu (vlevo) a eliptického paraboloidu (vpravo).
Důvodem, proč se geometrie chová na všech těchto objektech podobně, je, že jsou to zástupci ploch s tzv. kladnou křivostí. V diferenciální geometrii se zavádí veličina nazývaná Gaussova křivost. Počítá se v každém bodě plochy a dává nám informaci o tom, jak „moc“ je plocha v daném bodě zakřivena. Jak jsme už zvyklí, nebudeme se zabývat složitými matematickými definicemi (ale zájemci se mohou více dozvědět například na Wikipedii) a místo toho si ukážeme konkrétní příklady. V případě sféry o poloměru \(R\) vychází Gaussova křivost jako \(K=1⁄R^2\) v každém bodě, všude tedy dostáváme stejné kladné číslo. A není divu, protože sféra je plně symetrická („vypadá z každé strany stejně“), takže dává smysl, že „míra zakřivení“ je v každém bodě stejná. Zároveň vidíme, že čím má sféra menší poloměr, tím víc je zakřivena, což je také vcelku přirozené.
Elipsoid či paraboloid již zjevně nejsou zakřiveny všude stejně a nejedná se tedy tím pádem o plochy konstantní křivosti. I když se ale křivost bude v rámci těchto ploch měnit, bude vždy kladná. Například rotační paraboloid na obrázku 4.15 vpravo vznikl rotací paraboly \(z(x)=-x^2+8\) kolem svislé osy. Můžeme si to představit tak, že libovolný bod v rovině \(xy\) vytáhneme do výšky podle předpisu \(z(x,y)=-(x^2+y^2)+8\). Například v počátku o souřadnicích \([0,0]\) vychází výška plochy rovná \(8\) (v daných jednotkách). V bodě \([1,1]\) už je to \(6\) atd. Každý bod na ploše tak můžeme v tomto případě identifikovat jen podle příslušných dvou souřadnic v rovině \(xy\) (sami si můžete rozmyslet, že třeba u sféry by tento postup již nefungoval, protože by přiřazení nebylo jednoznačné). Gaussova křivost pro tento paraboloid pak podle Wolfram Mathworld (v odkazu najdete obecné vztahy závislé na dvou parametrech \(a\) a \(b\). V našem případě je \(a=b=1\)) vychází \begin{equation*}\tag{4.5}\label{4.5} K(x,y)=\frac{4}{(1+4x^2+4y^2)^2} , \end{equation*} což je opět pro libovolný bod paraboloidu kladné číslo. Mimochodem, zde sice chápeme plochu paraboloidu jako vnořenou do třírozměrného prostoru, což je postup, který jsme si zakázali, ale děláme to jen pro lepší představu a zejména jednoduchou interpretaci vztahu. Samotné vnoření nijak nevyužíváme.

Obrázek 4.16 Praktická ukázka dvou rovnoběžek na válcové ploše.
Patrně pro nikoho nebude překvapením, že pokud bychom Gaussovu křivost spočítali pro rovinu, dostaneme v každém bodě nulu. To odpovídá naší přirozené představě, že rovina není nijak zakřivená. Platí zde eukleidovská geometrie, jak ji známe. K tomuto závěru bychom mohli dospět i úvahou, co by se stalo s křivostí sféry, kdybychom zvětšovali její poloměr nade všechny meze. Zmíněný výraz 1/R^2 by byl samozřejmě čím dál menší a menší a postupně by se přibližoval k nule. To proto, že dostatečně velkou sféru bychom lokálně nedokázali rozlišit od roviny (podobně, jako se nám to může stát na naší planetě, o čemž se ještě zmíníme). Když řeknete, s jakou přesností jste schopni měřit vzdálenosti, vždy lze najít takovou hodnotu poloměru sféry, aby byla její odlišnost od roviny v libovolné konečně velké oblasti menší. Je ale zajímavé, že rovina není jediný případ plochy s tzv. nulovou křivostí. Krásným příkladem je plášť válce nebo spíš, abychom se vyhnuli problémům s okraji, nekonečná válcová plocha. Můžeme si velmi snadno vyzkoušet, že geometrická tvrzení \eqref{4.2} dopadnou na válcové ploše stejně jako v rovině. Vezměme si kupříkladu součet vnitřních úhlů v trojúhelníku. Narýsujeme-li na rovný papír trojúhelník, víme jistě podle eukleidovské geometrie, že součet jeho vnitřních úhlů bude \(180^°\). Tento papír nyní můžeme vzít a přiložit na zvolenou válcovou plochu (například na plášť válcového koše – případně můžeme papír jen ohnout do válce). Papír se tím nijak nepotrhá, nedeformuje, pouze se ohne v prostoru. Narýsovaný trojúhelník tím nezmění své vlastnosti, původní úsečky již sice nejsou přímé v prostoru, ale stále tvoří nejkratší spojnice daných bodů, tentokrát ale na válcové ploše. Vytyčené vnitřní úhly ohnutím papíru nezmění svou velikost, takže jejich součet musí být stále \(180^°\). Podobně si můžeme vyzkoušet i tvrzení o rovnoběžkách. Narýsujeme-li na papír dvě rovnoběžky a opět vytvoříme válcovou plochu, stanou se z přímek geodetiky na válcové ploše – spirály. Stále ale bude platit, že jejich vzájemná kolmá vzdálenost se nemění. Opět se zde dostáváme k rozdílu mezi vnější geometrií a vnitřní. Rovina a válcová plocha se zjevně liší svou vnější geometrií – každá z nich je jinak zakřivená v prostoru. Jejich vnitřní geometrie je ale stejná.
Zároveň jsme získali dobrý praktický návod jak poznat, že má nějaká plocha nulovou křivost. Pokud ji dokážeme zabalit do papíru, aniž by se papír potrhal či nějak jinak zpřehýbal (dovoleno je pouze jeho ohýbání), musí mít daná plocha nulovou křivost. Například je zaručeno, že se vám nikdy nepodaří zabalit kouli do papíru tak, abyste ho nemuseli stříhat či mačkat. Rozhodně si to zkuste. Vezměte například pomeranč nebo mandarinku a zkuste je zabalit do listu papíru bez jeho pomačkání či trhání. Případně zkuste ten pomeranč opatrně oloupat a slupku pak vyhladit do roviny, aniž by se potrhala. Mimochodem, tento problém nemožnosti zabalení koule do papíru, aniž by se nějak deformoval, má přímou souvislost s kartografickým problémem, jak věrně zobrazit povrch naší planety na rovný papír nebo monitor počítače. Mapy s malým měřítkem není prakticky nutné nějak upravovat, ale pokud si otevřete atlas s mapou celého zemského povrchu, je hned jasné, že tady už muselo dojít k velkému zkreslení a překroucení, abychom dostali zemský povrch do roviny. Rovinné mapy nám sice neukazují povrch Země potrhaný, ale při jejich vytváření jsou použity chytré matematické transformace, které na správných místech upraví skutečné rozměry tak, aby vše fungovalo. Příkladem toho mohou být čáry konstantní zeměpisné šířky (už zmíněné rovnoběžky), které se na obdélníkových mapách směrem na jih a na sever často zhušťují nebo mění svůj tvar.
Viděli jsme plochy s kladnou křivostí a s nulovou křivostí, nyní se podíváme na plochy se zápornou křivostí. Ty už nejsou tak blízké naší běžné zkušenosti. Často zmiňovaným příkladem je hyperbolický paraboloid zvaný také sedlová plocha – obrázek 4.17 (podobnost s koňským sedlem je zde vcelku zjevná). Přímou zkušenost s koňským sedlem má dnes již asi málokdo z nás, nicméně na tento zajímavý tvar můžeme narazit také u brambůrků značky Pringles. Ne, že bychom zde chtěli dělat reklamu nějaké konkrétní značce, ale ukazuje se, že jiné brambůrky prodávané v tubě nemají tvar hyperbolického paraboloidu, nýbrž pouze části válcové plochy (jinými slovy jsou prohnuty pouze v jednom směru na rozdíl od sedla, které je prohnuto ve dvou na sebe kolmých směrech) – ověření tohoto tvrzení necháme na čtenářově vlastním výzkumu.

Obrázek 4.17 Vlevo nahoře: Vykreslení sedlové plochy jako 3D grafu. Vpravo nahoře: 3D-vytištěná pomůcka demonstrující rozbíhání původně rovnoběžných geodetik a vlevo dole porovnána s kartonovým modelem. Vpravo dole: Obrázek pro změnu z počítačové animace demonstruje tři geodetiky tvořící na sedlové ploše trojúhelník. Součet jeho vnitřních úhlů je zjevně menší, než kdyby byl trojúhelník vytvořen v rovině.
Představme si sedlovou plochu opět jako 3D graf, tedy že každému bodu v rovině xy určíme konkrétní výšku jako souřadnici \(z\). Jednou možností této funkce \(z(x,y)\) je \begin{equation*}\label{4.6}\tag{4.6} z(x,y)=x^2-y^2. \end{equation*} Alternativně bychom mohli ve vzorci \eqref{4.6} prohodit znaménka u souřadnic, čímž plochu otočíme o \(90^°\) (můžete si to vyzkoušet například zde). Gaussovu křivost v tomto případě lze nalézt jako (opět podle Wolfram Mathworld, opět v našem případě oproti odkazu používáme \(a=b=1\)): \begin{equation*}\label{4.7}\tag{4.7} K(x,y)=-\frac{4}{(1+4x^2+4y^2)^2}. \end{equation*} Vidíme, že Gaussova křivost vychází v každém bodě opravdu záporná, nikoli však ve všech místech stejná. Abychom nyní mohli vyzkoušet vnitřní geometrii této plochy, tj. ověřit jak dopadnou geometrická tvrzení \eqref{4.2}, potřebujeme rozhodně větší a odolnější model než je bramborový lupínek. Zároveň naprostá většina z nás nemá snadný přístup ke koňským sedlům. Jeden snadný způsob, jak plochu vytvořit, je 3D tisk (samozřejmě snadný jen pokud máme k dispozici 3D tiskárnu; nemáme-li ji k dispozici, můžeme vytvořit alespoň dostatečně přibližný model z kartonu. Na obrázku 4.17 vlevo dole vidíme porovnání vytištěného parabolického hyperboloidu s kartonovým modelem. Oba také ukazují, že původně rovnoběžné geodetiky se rozbíhají (na rozdíl od kladně zakřivených ploch, kde se sbíhaly). Stejně tak je možné ukázat pomocí tří geodetik, že součet vnitřních úhlů v trojúhelníku je vždy menší než \(180^°\) (na obrázku vpravo dole vidíme obrázek z appletu, který si můžete vyzkoušet i vy). O něco náročnější, ale stále možné je ukázat, jak to bude se vztahem kružnice v ploše a jejího poloměru. Samozřejmě se zde musíme opřít o obecnou definici kružnice jako množiny bodů, jejichž vzdálenost od zvoleného středu je stejná. I zde by naše geometrická zkouška dopadla v jistém slova smyslu „opačně“ než u kladně zakřivených ploch, obvod kružnice bude větší než její poloměr vynásobený \(2π\).
Dalším příkladem záporně zakřivené plochy je například jednodílný hyperboloid, který známe jako typický tvar chladících věží v elektrárnách (obrázek 4.18 vlevo). Samozřejmě existují i plochy, které mají oba druhy křivosti. Jak jsme si říkali, křivost je bodová vlastnost, takže v různých bodech plochy může být různá, včetně svého znaménka). Existuje i vcelku jednoduchý trik, jak na první pohled odhadnout, zda je plocha v daném místě zakřivená kladně či záporně. Vytvořme v daném místě dvě navzájem kolmé geodetiky (pro praktickou zkoušku poslouží i například vaše ukazováčky). V místě s kladnou křivostí budou tyto křivky z našeho pohledu shora „zatáčet“ na stejnou stranu, například obě od nás nebo obě směrem k nám. U záporně zakřivené plochy budou „zatáčet“ na opačné strany (srovnání vidíme na obrázku 4.18 vpravo). Zkuste například pomocí tohoto testu určit typ křivosti na vnější a vnitřní straně banánu.

Obrázek 4.18 Vlevo: Jednodílný hyperboloid.
Vpravo: Navzájem kolmé geodetiky na záporně a kladně nabité ploše.
Existuje samozřejmě mnoho dalších způsobů jak zkoumat zakřivení a mnoho jiných příkladů zajímavých ploch. Účelem této podkapitoly bylo ale pouze poukázat na existenci různých druhů zakřivení a jejich účinků na vnitřní geometrii. Pojďme se proto nyní už posunout zase o kousek dál na naší cestě za obecnou relativitou. Chcete-li toho o zakřivení vyzkoušet více, podívejte se na Geometrické aktivity a modely.
Gravitace a geometrie
Jakkoli se naše geometrická odbočka může zdát zajímavá, jistě je na místě vysvětlit, proč k ní na naší cestě k základům obecné relativity muselo dojít. Způsob tohoto vysvětlení ale silně závisí na našich předchozích znalostech. Není v našich silách přednést rigorózní, ale matematicky komplikované argumenty, které bychom nalezli ve vysokoškolských učebnicích. Namísto toho půjdeme opět cestou připodobnění a odkazů na věci, které již známe. Berte tedy tuto kapitolu ne jako důkaz, že relativistický pohled na gravitaci je nutně geometrický, ale jako ukázku, že je popisovaný geometrický přístup možný a oprávněný. Vlastně tak vytváříme konkurenci newtonovskému pohledu na gravitaci a později tyto dvě teorie rozsoudíme, jak to má být - v reálném experimentu.
Představme si těleso, které se volně (tj. bez působení vnějších sil) pohybuje vesmírem. Jak už bylo řečeno dříve, takové těleso se pohybuje podle prvního Newtonova zákonu rovnoměrně přímočaře (tj. pořád stejně rychle po přímce). Pokud se pak těleso dostane do gravitačního pole například planety, jeho trajektorie se zakřiví (obrázek 4.19 vlevo nahoře). Podobně, pokud bychom v prázdném mezihvězdném prostoru vyslali dvě tělesa rovnoběžně stejnými rychlostmi, jejich trajektorie budou pochopitelně rovnoběžné přímky a vzdálenost mezi tělesy bude během pohybu prakticky stejná. Pokud ale stejný pokus uskutečníme například v dostatečné blízkosti nějaké planety, tělesa se k sobě začnou přibližovat či oddalovat podle toho, kterým směrem je vyšleme (obrázek 4.19 vlevo dole a vpravo ilustruje dvě takové situace). Klasická fyzika si tyto změny v chování těles vysvětluje jednoduše. V gravitačním poli na tělesa působí gravitační síla, takže už nejsou volná a jejich dráhy jsou tím pádem nutně zakřiveny.
Relativita se na celou věc dívá jinak. Gravitaci si nevysvětluje jako přitažlivou sílu způsobenou planetou, ale jako změnu geometrie v jejím okolí. Jistě vám neunikla podobnost mezi chováním trajektorií těles v gravitačním poli a geodetik na zakřivených plochách. Stejně jako na zakřivené ploše nelze nakreslit přímku, nemůže se těleso čistě pod vlivem gravitace obecně pohybovat v prostoru po přímce (musela by na těleso působit ještě nějaká jiná síla, například raketových motorů, která by musela velmi přesně kompenzovat působení gravitace). I původně rovnoběžné trajektorie se budou přibližovat či oddalovat podobně jako geodetiky na zakřivených plochách.
Na druhou stranu, jistě si vzpomenete na začátek kapitoly 4.1, kde jsme předem nastínili náš plán ukázat, že gravitace je zakřivení prostoročasu. V tom případě vám jistě připadá zvláštní, že tu najednou mluvíme o gravitaci jen v souvislosti se zakřivením prostoru. My zde ale zatím pouze poukazujeme na jistou podobnost. Brzy si ukážeme, že prostorové zakřivení samo o sobě nestačí a opravdu je třeba uvažovat o zakřivení prostoročasu. Snažíme se jen postupovat pomalu a pořádně.

Obrázek 4.19 Vlevo nahoře: Trajektorie volně se pohybujícího se tělesa je přímka. Za přítomnosti gravitace je ale trajektorie zakřivena.
Vlevo dole a vpravo: Dva příklady situace, kdy vypustíme v gravitačním poli dvě tělesa rovnoběžnými směry. Bez gravitace by jejich trajektorie byly rovnoběžné přímky, za přítomnosti gravitace se tyto zpočátku rovnoběžné trajektorie k sobě přibližují či oddalují, podle směru vypuštění. V obou případech pouze upozorňujeme na jistou podobnost se zakřivenou geometrií. Netvrdíme, že dané chování je přesně stejné.
No dobře, řeknete si. Jistá podobnost mezi neeukleidovskou geometrií a chováním těles v gravitačním poli by tu byla. Ale to není nijak zvlášť přesvědčivý argument, něco podobného bychom mohli tvrdit pro jakoukoli působící sílu, ne? Ve skutečnosti ale ne. V podkapitole o slabém principu ekvivalence jsme si ukázali jednu velmi důležitou vlastnost gravitace – její univerzálnost. S využitím Newtonova gravitačního zákona \eqref{4.1} a experimentálně potvrzované rovnosti gravitační a setrvačné hmotnosti jsme došli k závěru, že v daném místě bude gravitace (na rozdíl například od elektrické síly) na všechna tělesa působit stejně. Vezměme si jako názornou analogii geometrii terénu. Dává nám jistě smysl, že kopec je v nějakém daném místě stejně strmý pro každého a je jedno, zda jdete pěšky, jedete autem nebo na kole. Jak by bylo podivné, kdyby v analogii s elektrickou silou byl kopec ve stejném místě pro různé lidi různě strmý a pro některé by tam vůbec nebyl (jako když na neutrony elektrická síla nepůsobí). Na rozdíl od jiných přírodních sil, spojení geometrie prostoru (ale ve skutečnosti, jak ukážeme později, prostoročasu) a gravitace tedy dává přinejmenším smysl, i když se může zdát na první pohled jako zbytečné komplikování situace. (Mimochodem, ve vší otevřenosti přiznejme, že existuje i fyzikální teorie, která se snaží vysvětlit nejen gravitaci, ale i elektromagnetické působení geometrickým způsobem. Oproti OTR k tomu potřebuje ještě o jednu hypotetickou dimenzi více. Nazývá se Kaluzova-Kleinova teorie. Její platnost ale není obecně uznávána a ani my se jí zde nebudeme věnovat. Zájemci se o ní mohou dozvědět více například na příslušné stránce Wikipedie.)
Další argument podobnosti gravitačního působení a zakřivených ploch či prostorů vychází z principu ekvivalence(i když striktně vzato předchozí argument univerzálnosti gravitace je také jeho důsledkem). Podle něj jsme schopni v každém místě gravitačního pole vytvořit lokální inerciální systém (LIS). Ten má v podstatě jen dvě omezení, musí volně padat a nesmí být příliš rozlehlý. Splníme-li tyto dvě podmínky, účinky gravitace pro nás „zdánlivě“ zmizí. Slovo zdánlivě je zde trochu komplikované. Na jednu stranu pro nás uvnitř LISu doopravdy zmizí účinky gravitace (člověk ve volně padajícím výtahu či v ISS gravitaci doopravdy necítí a nenaměří). Na druhou stranu při pohledu ze zemského povrchu (což je pohled, který se nám jistě neustále vkrádá na mysl, protože jsme na něj tolik zvyklí) stále účinky gravitace na daný LIS vidíme – volným pádem se přibližuje k zemi, anebo je jeho trajektorie zakřivena při pohybu na oběžné dráze. Již jsme se o tomto zdánlivém rozporu způsobeném odlišnými vztažnými soustavami zmínili v poznámce u slabého principu ekvivalence. Pro nás je ale důležitý pohled člověka v LISu. Podstatné nyní je, že jsme teoreticky schopni takových LISů vytvořit v okolí naší planety celou spoustu a pozorovatelé uvnitř nich neucítí gravitaci. Protože jsou ale tyto soustavy lokální, pozorovatelé v jednom LISu nebudou souhlasit se závěry pozorovatelů v jiném. Na obrázku 4.20 vlevo vidíme dvě takové soustavy, které jsme ve stejný okamžik nechali volně padat. Pozorovatelé v obou z nich necítí účinky gravitace a jakékoli těleso (třeba kámen), které vypustí z klidu, vůči nim v klidu zůstane (protože z pohledu Země padají společně, vzpomeňme na princip ekvivalence), ale vůči vždy druhému z dvojice to pravda nebude. Například červený pozorovatel zjevně vidí, jak se kámen vypuštěný modrým pozorovatelem původně z klidu přibližuje. Červený pozorovatel ho tak nemůže zahrnout do své soustavy, protože pak by už nebyla inerciální. Symetrická úvaha platí i pro druhého pozorovatele.
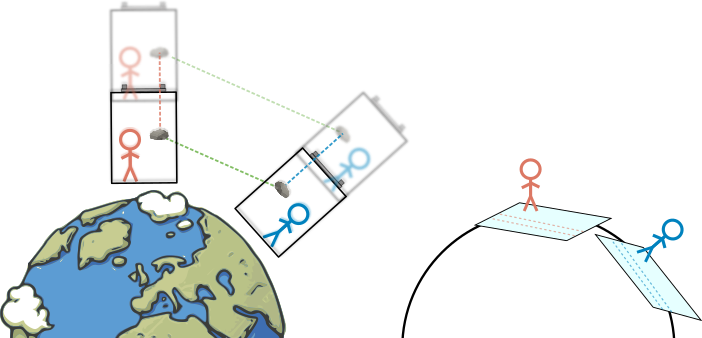
Obrázek 4.20 Pozorovatelé ve dvou lokálních inerciálních systémech v gravitačním poli mají mnoho společného s dvěma vzdálenými pozorovateli na zakřivené ploše, protože pro oba se v dostatečně malém měřítku neprojeví gravitace/zakřivení plochy. Jejich závěry jsou podobné, ale nejsou totožné.
Je to podobné jako když jsme na povrchu koule (obrázek 4.20 vpravo - ale tato úvaha by platila pro jakoukoli zakřivenou plochu, nemá to nic společného s tím, že planety a hvězdy jsou přibližně kulaté). Pokud se zaměříme na dostatečně malé území, budeme si připadat jako v rovině, a i všechna geometrie, kterou si na povrchu vymyslíme, bude fungovat nerozeznatelně od rovinné geometrie – rovnoběžky si udrží stále stejnou vzdálenost, nejkratší spojnice bodů bude úsečka apod. Nebude to zcela přesně pravda, ale odchylky budou tak malé, že to nepoznáme. Ve zcela stejné situaci bude někdo velmi daleko od nás (klidně třeba na opačné polokouli). Také jeho blízké body je možné spojit úsečkou a rovnoběžky zůstávají rovnoběžné, ale jeho rovnoběžky nebudou nikdy rovnoběžné s našimi, ať se snažíme jakkoli (leda, že by stál opravdu přesně na druhé straně sféry). Jinak řečeno, v každém místě sféry můžeme aproximovat povrch rovinou (v naší paralele bychom jí klidně mohli říkat lokální euklidovský systém, což má hezkou zkratku LES, ale těžko byste tento pojem hledali v nějaké odborné literatuře). V podkapitole o sférické geometrii jsme si ukázali, že na Zemi může náš LES být poměrně veliký, například jako velkoměsto, a sférická povaha Země se viditelně neprojeví. Například městští architekti v Berlíně a v Sydney tak mohou (odmyslíme-li si opět zvlnění terénu) klidně svá města považovat za ležící na rovině, ale jejich roviny nejsou vzájemně rovnoběžné. A chcete-li se dostat z Berlína do Sydney, sférická geometrie se už zákonitě projeví (vzpomeňte na obrázek 4.11). Vidíte tu podobnost s LISy a tedy s gravitací?
Připusťme nyní alespoň na chvilku, že na gravitaci se dá dívat jako na zakřivenou geometrii. Ale geometrii čeho vlastně?
Zakřivený...prostor?!
Nyní je třeba začít si zvykat na další velmi důležitou a silně abstraktní myšlenku. Myslíte si, že když může být zakřivená plocha, může být zakřivený i prostor?
Představit si skoro jakoukoli zakřivenou plochu nám nedělá problém, protože si ji prakticky vždy představujeme v prostoru. Je to pro nás naprosto přirozené, protože jsme se jako živočišný druh vyvinuli v trojrozměrném prostředí a naše mozky jsou skvěle uzpůsobeny pro prostorové vnímání světa. To je výborná vlastnost, pokud potřebujete přežít v přírodě či obecně normálně fungovat ve světě, ale v této chvíli je nám trochu překážkou. Jak si můžeme představit zakřivený prostor a je něco takového vůbec možné?
Je velmi pravděpodobné, že vám nedělalo problém alespoň přijmout existenci neeukleidovské geometrie na zakřivených plochách. Je vcelku zjevné, že nejkratší spojnice dvou bodů na sféře nemůže být přímka, protože jsme nuceni setrvávat na povrchu. Kdybychom se ale mohli provrtat dovnitř sféry, jistě bychom dokázali oba body spojit úsečkou, jak se patří, a byla by to nejkratší možná spojnice. Pokud bychom se nemuseli omezovat na nějakou plochu, můžeme v prostoru krásně identifikovat rovnoběžky, co se nikdy neprotnou, rýsovat trojúhelníky o tom správném součtu vnitřních úhlů, zkrátka eukleidovská geometrie zase funguje. Trojrozměrný prostor je samozřejmě eukleidovský, řekli bychom. Ale víme to jistě?
Vezměme opět příklad sféry. Pro dostatečně malou oblast jejího povrchu ji nedokážeme rozeznat od roviny. Zakřivené se zdá rovné. Běžně nám připadá směšné, když někdo tvrdí, že Země je placatá, ale jakmile se začneme bavit o geometrii prostoru, dostáváme se na výrazně nejistější půdu – o tvaru naší planety toho víme hodně, ale o celém vesmíru? Jen velmi málo. Mimochodem, tomu našemu známému „rovnému“ eukleidovskému prostoru se říká také plochý, ve smyslu ne zakřivený, což je vlastně trochu nešťastný překlad z anglického flat, protože plocha obecně může být zakřivená, ale vžité názvosloví už asi nezměníme. Plochost prostoru běžně předpokládáme a využíváme v každodenním životě – ve stavebnictví, letectví, kosmonautice, prakticky pořád. Nemáme ale zatím žádný pádný důkaz o tom, že by byl prostor plochý všude. Co když jsme ve stejné situaci jako na malém kousku sféry a skutečnost je jiná, než se zdá? Abychom dokázali rozlišit mezi rovinou a sférou v rámci vnitřní geometrie, musíme provádět měření přes dostatečně velké vzdálenosti, což už na Zemi umíme. Stejně tak bychom mohli časem provádět geometrická měření kolem naší planety nebo ještě později i napříč Sluneční soustavou. To je totiž jediný způsob, jak dostat odpověď na naši otázku. Na rozdíl od povrchu naší planety nedokážeme vystoupit mimo prostor, podívat se na něj z vyššího rozměru, plácnout se do čela a říct jednoznačné: „No jasně!“ Chceme-li odhalit skutečnou povahu prostoru, nezbývá nám než pečlivě proměřovat přes co největší vzdálenosti. Problém ovšem tkví v tom (pomineme-li náročnost takových měření), že i kdybychom s nějakou přesností dokázali platnost eukleidovské geometrie v naší soustavě, nic to nedokazuje o celém velkém vesmíru.
Vraťme se ale zase trochu zpět. Abychom pochopili obecnou teorii relativity, budeme si muset na myšlenku zakřivení prostoru zvykat. Dokonce to bude ještě horší, protože naším finálním cílem je zakřivení prostoročasu! Ale tam ještě nejsme. Nejprve vyřešme palčivou otázku, jak si takový zakřivený prostor představit. Na to existuje jednoduchá odpověď, která vás ale asi moc neuspokojí. Prostě si ho nepředstavujte. Respektive klidně to zkoušejte, ale nebuďte zklamaní, když vás z toho maximálně rozbolí hlava. Lidský mozek na něco takového není stavěný a představit si zakřivený prostor nedokáží často ani matematici, kteří se jím zabývají většinu svého života. Naštěstí velmi krásnou vlastností matematiky je, že ji můžeme zobecnit i do situací, které si už představit neumíme.
Když už si zakřivený prostor nepředstavíme, zkusme ho aspoň nějak popsat. A zde právě využijeme naše detailní úvahy o zakřivených plochách. Zakřivený prostor se bude od toho plochého lišit právě tak, jako se zakřivená plocha liší od roviny. Nebude zde fungovat eukleidovská geometrie. Dvě zpočátku rovnoběžné přímky se k sobě budou přibližovat či oddalovat. Součet vnitřních úhlů v trojúhelníku nebude rovný \(180^°\), vztah obvodu kruhu a jeho poloměru…, však už to dobře známe. Je asi zřejmé, že pokud bychom se ocitli v silně zakřiveném prostoru, naše běžné vnímání světa by bylo dost otřeseno. Podobné úvahy vypadají hodně jako vytažené z vědecko-fantastické literatury a určitě je nedokážeme dostatečně viditelně replikovat v našich podmínkách. To ale neznamená, že něco takového není možné. Matematikové jsou odborníci na popis silně abstraktního a těžko představitelného díky tomu, že matematika něčeho známého jde často zobecnit na něco neznámého. Nejen proto si v pozdější části této kapitoly prozradíme něco z matematického popisu zakřivených ploch a uvidíme, že jde velmi snadno zobecnit i na zakřivený prostor. Nemusíte se ale děsit. V našich fyzikálních příkladech se omezíme na situace, které dokážeme snadno vizualizovat. Naštěstí se jak v klasické mechanice, tak v relativitě ukazuje, že pokud nějaké těleso obíhá přibližně sféricky symetrický zdroj gravitace (jako třeba Země obíhá Slunce), bude dráha tohoto pohybu stále v jedné rovině. To se dá docela snadno pochopit. Představte si třeba satelit obíhající kulovou planetu. Dráha satelitu je stáčena gravitací, ale ta působí ve směru pomyslné spojnice satelitu a planety. Pokud tedy satelit vypustíme například v rovině rovníku, bude „zatáčet“ vždy jen směrem k planetě a nemá důvod uhnout ani nad severní ani nad jižní polokouli. Stejný argument můžeme uplatnit na jakoukoli jinou dvojici sféricky symetrického gravitujícího tělesa a jeho oběžnice a nemusí se nutně jednat ani o obíhání v rovníkové rovině. Proto pro nás bude těleso obíhající v rovině zásadně důležitým jednoduchým, ale přesto fyzikálně velmi relevantním příkladem.
Předveďme si to na té nejprimitivnější a přitom nejdůležitější vizualizaci základní myšlenky OTR. Budete k ní potřebovat jen tužku, papír a případně pravítko a nůžky, ale ty nejsou nutně potřeba. Celou situaci vidíme na obrázku 4.21. Vlevo máme připravenou kruhovou výseč, na kterou jsme narýsovali rovnou čáru procházející blízko středu ale ne přímo skrz něj. Rozložená výseč představuje plochý eukleidovský prostor, ve kterém platí zákony staré dobré eukleidovské geometrie. Fyzikálně to znamená, že není přítomno žádné gravitační pole a libovolné volné těleso se bude pohybovat rovnoměrně přímočaře (reprezentováno rovnou čarou). Nyní „zapneme“ gravitaci. Ve středu výseče se objeví například hvězda, která svou gravitací způsobí, že se prostor kolem ní zakřiví. Jak ale toto zakřivení zviditelnit? Stejně jako u zakřivených ploch, rovinu musíme „vytáhnout“ do třetího rozměru. ALE POZOR! Toto vytažení je jen pro naši lepší představu. Neznamená to, že se fyzikální pohyb bude najednou odehrávat i mimo původní rovinu. Když teď tedy zakřivíme kruhovou výseč tím, že z ní složíme plášť kužele (či chcete-li - čepičku), musíme se na trajektorii tělesa stále dívat, jako by byla v původní rovině – to znamená „shora“ (obr 4.21 vpravo).

Obrázek 4.21 Vlevo: Kruhová výseč reprezentující plochý eukleidovský prostor. Bez přítomnosti gravitace se pomyslné těleso pohybuje po přímce (vyznačená rovná čára).
Vpravo: „Zapnutím“ gravitace se prostor kolem gravitujícího tělesa zakřiví, což vizualizujeme složením výseče do pláště kuželu. Vidíme, že se zakřiví i trajektorie tělesa. Na celou situaci je ale třeba se dívat stále jako na dvourozměrnou (pohyb je pořád v původní rovině) – proto se na kužel musíme dívat shora.
Sami si můžete vyzkoušet, že čím víc papír zakřivíte, tím více se zakřiví i nakreslená trajektorie tělesa. Zároveň je úplně jedno, jestli špička pomyslného kužele míří k vám nebo od vás (tj. jestli papír prohnete k sobě nebo od sebe). V obou případech dostáváme stejný výsledek, protože nezáleží na orientaci této plochy, pouze její geometrii. Tato velmi jednoduchá ukázka demonstruje základní myšlenku obecné teorie relativity. Prostor je kolem hmotných těles zakřiven, což způsobuje zakřivení trajektorie pohybujících se těles.
Poznámka 4.5
Nutno dodat, že v této demonstraci s kuželem malinko podvádíme, či přinejmenším zatajujeme. Když jsme si představovali různé neeukleidovské geometrie, ukázali jsme si jednoduchý návod, jak poznat, zda má nějaká zakřivená plocha ve skutečnosti stejnou vnitřní geometrii jako rovina. Pokud na ni dokážeme přiložit papír, aniž by se potrhal nebo zmačkal, má daná plocha také nulovou křivost jako rovina. Jako příklad jsme si uvedli válcovou plochu a dalším příkladem je právě kuželová plocha – tedy plášť kužele. Snadno jej můžete obalit do papíru, až na jeden jediný bod – na jeho špičku. Tam neuspějete, protože papír byste museli všelijak komplikovaně zpřehýbat přes sebe. A to je i ten důvod, proč naše demonstrace s kuželem funguje. Libovolný ucelený kus pláště má stejnou vnitřní geometrii jako rovina (říkáme, že je lokálně plochý), ale na špičce je tzv. singulární bod – bod, kde náš popis geometrie moc dobře nefunguje. Schválně si zkuste představit čáru, která vede po plášti přímo na špičku. Kudy má čára pokračovat, až se tam dostane? Není to jasně dáno a i kdybychom si nějaký směr vybrali, čára bude zlomená a to komplikuje její matematický popis. Nechceme zde zbytečně zabíhat do technických detailů, ale podstata je, že kužel reprezentuje zakřivený „prostor“ jen díky své špičce. Můžete si sami vyzkoušet, jak se budou na kuželi chovat geodetiky (tj. třeba proužky papíru) vyslané rovnoběžnými směry. Pokud každou z nich namíříte z jedné strany singularity, protnou se podobně jako na kouli. Pokud je ale povedete obě na stejné straně od singularity, rovnoběžky, ač křivočaré, budou stále rovnoběžkami. Vyzkoušet si to můžete také v appletu.
Obecná relativita tedy popisuje gravitaci ne jako přitažlivou sílu působící mezi hmotnými tělesy (což je přístup klasické fyziky), ale právě jako toto zakřivení kolem hmotných těles. Představme si například planetu obíhající kolem hvězdy. Podle klasické fyziky je dráha planety zakřivována přitažlivou gravitační silou od hvězdy, což je našemu chápání docela blízké, ale na druhou stranu, jak jsme rozebírali na začátku kapitoly 4.1, má tento přístup své nedostatky. Podle OTR ve skutečnosti planeta opravdu letí stále „rovně“, ale protože hvězda ve svém okolí zakřivuje prostor, je celková trajektorie planety zakřivena podobně, jako kdybychom šli „stále rovně“ po povrchu koule. Proto se také v OTR i tělesa čistě pod účinkem gravitace nadále nazývají volná, protože jejich pohyb neovlivňuje žádné jiné než gravitační působení, ale to už v našem popisu není silou. Tuto představu ilustruje obrázek 4.22. Na podobné vizualizace můžeme narazit na internetu nebo v literatuře často. Pro lepší čitelnost je v nich prostor reprezentován pouze rovinou. V kapitole 4.3 se k tomuto modelu ještě vrátíme a ukážeme jeho přímou souvislost s relativistickými výpočty.
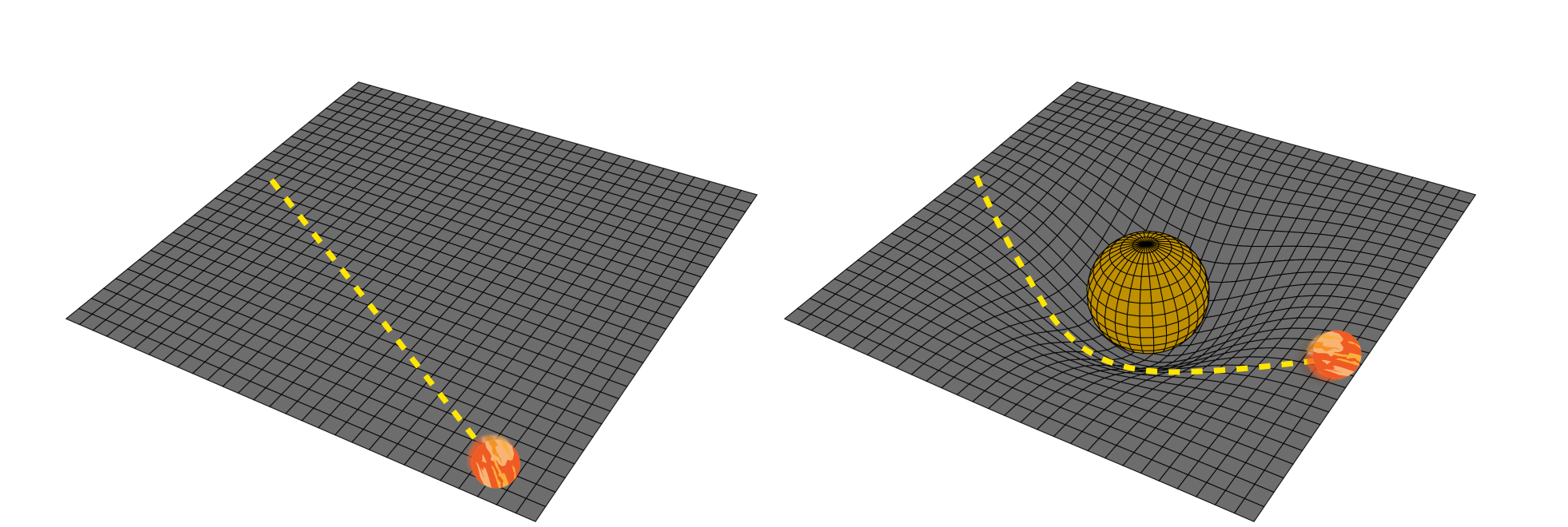
Obrázek 4.22 Vlevo: Podle OTR je prostor bez přítomnosti hmotných zdrojů nezakřivený (tzv. plochý) a všechna volná tělesa (dostatečně málo hmotná, abychom mohli zanedbat jejich vliv na zakřivení) se v něm budou pohybovat po přímkách.
Vpravo: V okolí gravitujících těles je prostor zakřivený, tj. jeho samotná geometrie není eukleidovská. Důsledkem toho se trajektorie volných těles (například planet v okolí hvězdy) zakřivuje, ačkoli se lokálně pohybují rovně.
Jistě se to zdá jako velký myšlenkový skok a je klidně možné, že si na tuto myšlenku budete muset chvíli zvykat. Na tom není nic špatného. Zakřivený prostor je fascinující představa, která se ale představuje velmi špatně. A bude to ještě zajímavější. Náš popis gravitace jako zakřivení prostoru totiž nevysvětluje zdaleka vše potřebné. Stačí si totiž vzít ten nejjednodušší druh pohybu v gravitačním poli – volný pád – a najednou jsme v úzkých. Na kuželu jsme totiž demonstrovali, že trajektorie pohybujícího se tělesa může být díky neeukleidovské geometrii prostoru zakřivena. Co když se ale těleso nehýbe? Když na kuželu uděláte tečku reprezentující těleso v klidu, nezačne se samo od sebe pohybovat. Nemá k tomu důvod! Nedokážeme tedy vysvětlit tu naši naprosto běžnou lidskou zkušenost, že pokud pustíme těleso z klidu, začne padat k zemi. A to by jistě nebyla dobrá teorie gravitace, kdyby nedokázala vysvětlit ani volný pád. Naštěstí to snadno napravíme. Už od začátku našeho povídání jsme mnohokrát zdůrazňovali, že relativita se zabývá prostorem i časem. A když už jsme nakousli podivné chování prostoru, je třeba dodat i čas.
Gravitační dilatace času
Vstřebat tak abstraktní pojem jako zakřivení prostoru jistě není jednoduché, nicméně se zakřivením prostoročasu je to ještě složitější. Ačkoli to z fyzikálního hlediska nedává tak dobrý smysl, pro lepší pochopení jsme si celou situaci rozdělili. Stejně jako jsme mluvili o zakřivení prostoru, zaměřme se nyní na zakřivení času. I když zakřivení… Ve spojitosti s časem, o kterém nemáme vůbec tendenci uvažovat geometricky, je toto slovo trochu neobratné. Vhodnější výraz je dilatace času. Tu už jsme vlastně potkali ve speciální relativitě. Patrně nejdůležitější a nepodivnější předpověď STR byla, že navzájem se pohybujícím inerciálním pozorovatelům nebude shodně plynout čas. OTR přidává další způsob, jak se vám i mně mohou rozejít i sebepečlivěji synchronizované hodinky, a samozřejmě bude nějak souviset s gravitací. Abychom tyto dvě dilatace času odlišili, nazvěme tu způsobenou vzájemným pohybem kinematická a tu, o níž se budeme bavit nyní, gravitační.
Začněme popisem reálného experimentu. V roce 1959 pánové Pound a Rebka na harvardské univerzitě provedli na první pohled velmi zvláštní pokus. U střechy své laboratoře umístili vysílač elektromagnetického záření (jednalo se konkrétně o gama záření vysílané radioaktivním izotopem železa \({}^{57}\text{Fe}\)) a pod něj ve svislé vzdálenosti \(22{,}5\:\text{m}\) umístili přijímač. Samozřejmě zde hodně zjednodušujeme, protože konkrétní detaily provedení experimentu nejsou pro naše povídání podstatné, rozhodně ale stojí za pročtení například na Wikipedii. Podstatné pro nás je, že umístění vysílače a přijímače v různé výšce nad zemí způsobilo, že přijímač zachytil jinou frekvenci elektromagnetického záření, než jaká vycházela z vysílače. Nejenom, že tuto změnu naměřili, ale ta i v rámci přesnosti měření odpovídala teoretické předpovědi obecné relativity. A tak abychom pochopili, co má společného gravitace, změna ve frekvenci elektromagnetického vlnění a podivné chování času, pojďme si celou situaci blíže rozebrat.

Obrázek 4.23 Ilustrace vysvětlení Poundova-Rebkova experimentu pomocí volně padajícího LISu. Detailní popis je uveden v textu.
Na obrázku 4.23 máme náčrtek situace. Využijeme opět pohled z lokální inerciální soustavy, kterou reprezentujeme volně padajícím výtahem. Abychom si situaci trochu zjednodušili, představme si, že LIS začíná volně padat v okamžiku \(t_1\), kdy vysílač vyšle EM vlnění o nějaké frekvenci \(f_1\). Jak už víme, uvnitř LISu nejsme pod vlivem gravitace, a proto se na experiment můžeme dívat očima speciální relativity. Podle jednoho z jejích základních postulátů se vůči nám EM záření pohybuje konstantní rychlostí c. O chvilku později, v čase \(t_2\), dopadá paprsek do přijímače u paty aparatury. Díváme-li se na situaci ze země, pohybuje se LIS podle fyziky volného pádu v okamžiku \(t_2\) rychlostí \(v(t_2)=g(t_2-t_1)=g\Delta t\) (obrázek 4.24 vlevo). Podle výsledku experimentu přijímač naměří jinou frekvenci přicházejícího EM vlnění, než byla vyslána, označme ji \(f_2\). Abychom ale pochopili proč tomu tak je, musíme se na situaci podívat právě z pohledu LISu (obrázek 4.24 vpravo). Protože pohyb je relativní, z padající soustavy pozorujeme, že je to země a s ní i přijímač, kdo se pohybuje směrem vzhůru rychlostí stejně velkou, ale opačnou, než je rychlost pádu výtahu vůči zemi. Jak už víme, EM vlnění se vůči nám v souladu se speciální relativitou pohybuje jednoduše rovnoměrně přímočaře svou stále stejnou rychlostí \(c\), ale vidíme, jak se přijímač pohybuje vlnění naproti. To je jeden z případů, kdy dochází k tzv. Dopplerovu jevu . Tak nazýváme měřitelnou změnu frekvence vlnění, pokud se pohybujeme vůči jeho zdroji či pokud se zdroj pohybuje vůči nám (případně obojí najednou). Nejčastěji zažíváme Dopplerův jev u zvuku kolem projíždějících aut (například u sirény ambulance je to dobře slyšet). Jak se k nám zdroj zvuku blíží, frekvence, kterou slyšíme (tj. kterou naměříme), se zvýší a jakmile auto projede kolem a začíná se vzdalovat, frekvence klesne (a je to právě ta prudká změna ze zvýšené na sníženou frekvenci, kterou nejvíce vnímáme). Podobně to funguje, i když bychom se vůči zdroji pohybovali my. Není to ale tak, že by například zmíněná siréna měnila výšku svého zvuku, rozdíl mezi vysílanou a naměřenou frekvencí je právě dán tím vzájemným pohybem, jak ilustruje například toto video. Proč k tomu dochází, je poměrně podrobně vysvětleno na odkazované stránce, takže se tím nyní nebudeme zdržovat. I když Dopplerův jev typicky známe právě ve spojení se zvukem, týká se každého druhu vlnění, tedy i toho elektromagnetického. Posun frekvence u světla a dalšího EM vlnění způsobený vzájemným pohybem je dobře znám například astronomům, kteří pomocí něj měří mimo jiné rotační rychlost hvězd nebo relativní rychlost vzdálených galaxií vůči Zemi.
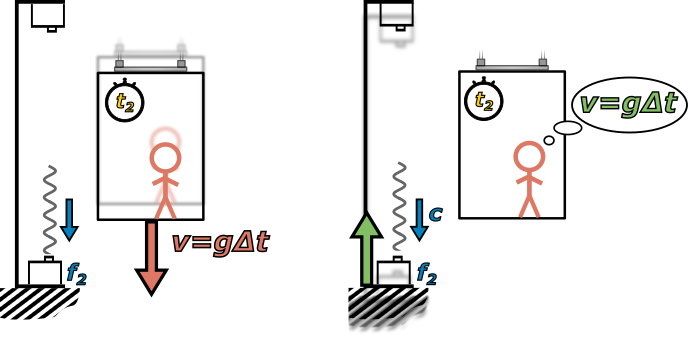
Obrázek 4.24 Vlevo: Z pohledu ze země padá výtah volným pádem kolem detektoru rychlostí \(v=g\Delta t\). Detektor v experimentu naměřil jinou frekvenci EM vlnění, než byla vyslána vysílačem, ale není jasné, proč tomu tak je.
Vpravo: Pohled na stejnou situaci zevnitř LISu. Odsud pozorujeme, že světlo se v souladu s postuláty STR pohybuje jednoduše konstantní rychlostí \(c\), a právě země spolu s přijímačem (s vysílačem samozřejmě taky, ale ten jsme už nechali za sebou) se pohybuje vzhůru rychlostí přesně opačnou, než s jakou se vůči zemi pohybuje výtah. Z fyziky vlnění plyne, že přístroj pak naměří vyšší frekvenci čistě díky tomuto vzájemnému pohybu, jak popisuje tzv. Dopplerův jev. Délka pohybu v obou případech je pro názornost silně přehnána.
Podle teorie Dopplerova jevu bude frekvence EM vlnění naměřená pozorovatelem/detektorem pohybujícím se rychlostí \(v\) \begin{equation*}\tag{4.8}\label{4.8} f_2=f_1\left(1+\frac{v}{c}\right), \end{equation*} kde \(c\) je naše stará známá rychlost EM vlnění a \(f_1\) je, jak už je řečeno výše, původní frekvence vyslaná zdrojem. Naměřená frekvence tedy bude větší než vyslaná, protože v závorce je znaménko plus. V případě EM vlnění se toto zvýšení frekvence nazývá modrý posuv (blue-shift), protože vzpomeneme-li si na obrázek elektromagnetického spektra na začátku třetí části, můžeme si všimnout, že zvýšení frekvence u světla vede ke změně barvy směrem k modrému okraji viditelného spektra (ve skutečnosti k fialovému okraji spektra, ale ustálilo se označení modrý posuv – pravděpodobně proto, že lidské oko není tolik citlivé na fialovou barvu a tak minimálně v historii nebývala při experimentech fialová část spektra tak dobře viditelná pouhým okem). Ale pozor, modrý posuv neznamená zbarvení do modra, například u zmíněného gama záření nemůže být o nějaké barvě řeč, je to prostě jen označení pro naměřené zvýšení frekvence EM vlnění způsobené vzájemným pohybem zdroje a pozorovatele (například světlo vzdálených hvězd, které se k nám přibližují, vykazuje modrý posuv). Anebo, jak jsme nyní viděli, ho může způsobit i gravitace. Jednoduše řečeno, „padá-li“ světlo v gravitačním poli, naměříme jeho frekvenci vyšší, než s jakou bylo vysláno zdrojem.
Celá situace funguje ale i obráceně. Pokud bychom v Poundově-Rebkově experimentu umístili vysílač dolů a nechali světlo „šplhat“ gravitačním polem vzhůru, zachytí detektor jeho frekvenci menší. V analogii s prvním případem se této situaci říká rudý posuv (red-shift). Například díky změřenému rudému posuvu světla přicházejícího z většiny vzdálených galaxií astronomové poprvé usoudili, že se od nás většina galaxií vzdaluje – jedná se tedy o rudý posuv způsobený vzájemným pohybem nás a dané galaxie. A protože se ukázalo, že typicky čím je od nás nějaká galaxie dále, tím rychleji se od nás vzdaluje (z naměřeného rudého posuvu se dá naše vzájemná rychlost vypočítat), vedla tato měření v první polovině dvacátého století k vyslovení hypotézy o rozpínání vesmíru. To už ale moc odbíháme.
Vzorec \eqref{4.8} můžeme dále pro náš případ upravit. Rychlost přijímače v okamžiku \(t_2\) je podle pozorovatele v padající soustavě \(v=g\Delta t\). Zároveň víme, že \(\Delta t\) je čas letu EM vlnění mezi vysílačem a přijímačem. Pokud jejich vzájemnou vzdálenost (tedy jejich výškový rozdíl) označíme jako \(h\), platí pro čas letu paprsku \(\Delta t=h/c\). Dohromady \begin{equation*}\tag{4.9}\label{4.9} f_2=f_1\left(1+\frac{gh}{c^2}\right). \end{equation*} Zkusme si rychlý odhad. V Poundově-Rebkově experimentu bylo \(h=22{,}5\:\text{m}\). Relativní změna frekvence podle \eqref{4.9} pak bude \begin{equation*} \frac{\Delta f}{f_1}=\frac{f_2-f_1}{f_1}=\frac{gh}{c^2}\dot{=}2{,}5\cdot10^{-15}, \end{equation*} neboli \(250\) biliardtin procenta. To je opravdu neuvěřitelně malá změna a ukazuje nejenom, jak jsou tyto změny v našich podmínkách pozemské gravitace miniaturní, ale hlavně jak precizně a chytře musel být celý experiment proveden, aby bylo možné něco takového naměřit.
Teď ale přichází ta zásadní úvaha. Jak souvisí podivné chování EM vlnění pod vlivem gravitace a běh času? Předně si musíme uvědomit, co to vlastně znamená frekvence vlnění. Není to ve své podstatě nic jiného než počet vrcholků vlny, které zachytíme za jednu sekundu. Když slyšíme zvuk o frekvenci \(100\:\text{Hz}\), znamená to, že na náš ušní bubínek naráží rozkmitaný vzduch stokrát za sekundu. Střídavé napětí v zásuvkách kmitá s frekvencí \(50\:\text{Hz}\), takže padesátkrát za sekundu dosáhne svého maxima. Když tedy říkáme, že vysílač vyšle signál o frekvenci \(f_1\), máme tím na mysli, že \(f_1\) krát za sekundu nastane „hřbet“ vyslané světelné vlny. Cestou k přijímači se ale tyto „hřbety“ nemají kam ztratit. Po cestě není žádná překážka, která by ovlivnila průběh vlny samotné. Jestliže přijímač naměří vyšší frekvenci, to znamená více vrcholů vlny za sekundu, znamená to, že má delší sekundu než vysílač. Jak jinak si tento úbytek frekvence vysvětlit. Delší sekunda znamená pomaleji plynoucí čas (zatímco někde jinde uplyne \(60\) sekund, zde uplyne třeba jen \(58\)). To je to, čemu říkáme gravitační dilatace času. Jedná se o čistě gravitační efekt, nikoli o nám již známou dilataci času ze speciální relativity způsobenou vzájemným pohybem. Tu jsme zde mimochodem pro snadnější pochopení situace zanedbali, protože vzájemná rychlost dvou uvažovaných soustav je po celou uvažovanou dobu experimentu velmi malá, což si čtenář jistě rychlým výpočtem s využitím vzorců výše dokáže ověřit sám.
Myšlenka, že například v různé výšce nad zemí plyne čas různě, se nepřijímá snadno. Bylo zapotřebí mnohem více experimentů, než byla obecně fyziky přijata. Mimochodem, v našem uvažování jsme nijak nemluvili o způsobu měření času, takže platí nezávisle na konstrukci našich měřících přístrojů, stejně tak pro mechanické hodiny jako biologické nebo fyzikální děje. Gravitace zpomaluje čas bez ohledu na to, jakým způsobem ho měříme. V místě s nižším gravitačním potenciálem (to znamená v menší výšce nad zemí, například u paty stožáru, kde byl přijímač) plyne čas pomaleji než v místě s vyšším potenciálem (vysílač na špičce stožáru). Dokonce dnes existují již tak přesné atomové hodiny, že gravitační dilatace času byla ověřena na atomech, jejichž rozdíl výšky byl pouhý \(1\:\text{mm}\)!
V další kapitole, až budeme umět i něco opravdu relativisticky spočítat, se k této problematice a k reálným experimentům ještě vrátíme. Prozatím si na tu představu jen tak pomalu zvykejme. I když zas tak pomalu vlastně ne, protože my jsme přece začali o gravitační dilataci času mluvit právě proto, aby náš popis gravitace byl úplný. Zakřivení prostoru kolem hmotných těles (jakkoli se může zdát na první pohled podivné a složité) dokáže sice vysvětlit mnoho o gravitaci, ale ne všechno. Nedokázali jsme jím vysvětlit volný pád. Nyní ale k našim úvahám můžeme přidat poznatek, že v přítomnosti gravitace neplyne čas všude stejně. A schválně to řekneme trochu jinak. Ve třetí části o STR jsme schválně strávili nějaký čas popisem, jak byl čas povýšen na rozměr rovný s prostorovými. Zavedli jsme prostoročas. Důvodem bylo, že pak dostávají rovnice a vlastně i celková filozofie STR krásný a ucelený nádech. Zavést prostoročas nebyla nutnost, ale pokud si na tuto myšlenku zvykneme, vše se ve výsledku zjednoduší. Podobné to bude i teď. Již jsme strávili pěknou řádku stran rozebíráním plošné a následně prostorové křivosti. Říkáme-li, že je prostor zakřiven, máme tím na mysli, že se geometrie – tedy samotný prostor – nechová v každém bodě stejně. A nyní jsme (zatím jen stručně) zjistili, že ani čas se nechová v přítomnosti gravitace všude stejně. Čas je tedy v okolí gravitujících těles také zakřiven. Ale neděste se, tím nutně netvrdíme, že čas je něco reálně geometrického, co může být křivé, máme tím na mysli právě přesně jen to, že čas neplyne v každém místě stejně. Abychom ale mohli propojit naše prostorové a časové úvahy, je výhodné o obojím mluvit ve stejné řeči. V našem případě je to právě v řeči geometrie.

Obrázek 4.25 Při „vypnuté“ gravitaci se výška kamene s časem nemění. Jejím grafem je tedy konstantní funkce.
Nyní se konečně dostáváme k tomu volnému pádu. Vezměme si velmi jednoduchou situaci, kdy máme kámen v klidu v nějaké počáteční výšce nad zemí. V rámci našeho myšlenkového experimentu prozatím vypneme gravitaci, takže kámen stojí nehybně ve vzduchu. Zkusme si nyní nakreslit graf závislosti výšky kamene nad zemí – označme ji \(h\) - na čase, tedy \(h(t)\). Jelikož se prozatím výška nijak nemění, mělo by se pochopitelně jednat o graf konstantní funkce (obrázek 4.25). Graf závislosti nějaké veličiny prostorového charakteru (v našem případě výšky) na čase pro nás snad není nic neobvyklého. Možná vás ale překvapí, že jsme právě načrtli jednoduchý případ tzv. prostoročasového diagramu (ten se sice v relativitě konvenčně kreslí s časovou osou svisle, ale to na věci nic nemění), kde jeden rozměr reprezentuje čas a druhý prostor (pro jednoduchost omezený jen na jednu prostorovou dimenzi, abychom nemuseli „kreslit“ tří- či čtyřrozměrné obrázky – i kdybychom to uměli). Takové diagramy se kreslí zejména už ve speciální relativitě, ale my jsme ho až dosud k ničemu nepotřebovali.
Pokud by měly obě osy v grafu prostorový význam, například souřadnice \(x\) a \(y\), tedy konvenčně vodorovná a svislá vzdálenost, křivka grafu by odpovídala trajektorii tělesa v prostoru. To jsme viděli například u vodorovného vrhu na obrázku 4.4. Analogicky odpovídá v případě prostoročasové diagramu zobrazená křivka trajektorii v prostoročasu, tzv. světočáře. Prakticky řečeno obsahuje informaci, jak se těleso pohybuje v prostoru a jak mu plyne čas (jinými a trochu návodnými slovy: jak se pohybuje v čase).
Poznámka 4.6
Zde je třeba říci, že samozřejmě čistý fyzikální význam má jen pohyb v prostoru. Trajektorie tělesa v prostoru je křivka spojující všechny body, kterými těleso prošlo, a tyto body existují nezávisle na tělesu. U trajektorie v prostoročase je tomu jinak. Jak už víme ze třetí části, prostoročas není tvořen jednotlivými body, ale tzv. událostmi (konkrétní místo a konkrétní čas). Světočára tělesa je tedy „spojnice“ všech událostí, kdy dané těleso bylo na daném místě v daný čas. O okamžik později je těleso o kousek jinde, což odpovídá jiné události. I kdyby stálo těleso na místě, nebude jeho světočára jeden bod, protože čas plyne pro těleso vždy. Mluvíme-li tedy o pohybu v prostoročase, jedná se o matematickou konstrukci, která nám pomáhá se lépe v situaci orientovat, a ne přímo reálný pohyb (ten je ale ve světočáře zahrnut také).
Světočára kamene na obrázku 4.25 je přímka, podobně jako je přímkou trajektorie volné částice v prostoru. Je to proto, že situace bez gravitace odpovídá plochému (tj. nezakřivenému) prostoročasu – přesně tomu, jaký jsme popisovali v části o speciální relativitě. Když nyní pomyslně „zapneme“ gravitaci, prostoročas se zakřiví. Celá situace je nyní analogická aktivitě na obrázku 4.21, kdy jsme účinek zakřivení na trajektorii tělesa demonstrovali složením papírové plochy do pláště kužele. Rozdíl je v tom, že nyní nezakřivujeme čistě prostor a tím prostorovou trajektorii tělesa, nýbrž prostoročas a tím pádem jeho světočáru. Abychom mohli tuto zásadní myšlenku celého našeho povídání demonstrovat, potřebujeme zakřivit i náš prostoročasový diagram. Můžeme ho tedy nakreslit na povrch, o kterém víme, že je jeho vnitřní geometrie odlišná od listu papíru.

Obrázek 4.26 Demonstrace zakřiveného prostoročasového diagramu. Světočára tělesa je geodetikou – tedy nejpřímější možnou "trajektorií" v zakřiveném prostoročase. Kámen se tím pádem nutně dostává na nižší výšku – padá.
To je například naše stará známá sféra, anebo, jak už víme, jakákoli sféře podobná plocha. Jeden konkrétní příklad vidíme na obrázku 4.26. Zde jsme na povrch nafouknutého balónku předkreslili osy prostoročasového diagramu. Na zakřiveném balónku samozřejmě nemůžeme realizovat souřadnicové osy jako vzájemně kolmé přímky, ale už víme, že zobecněním přímky je geodetika, kterou jsme na plochách napodobovali pomocí provázku nebo pruhu papíru. Osy pro nás tedy budou části dvou geodetik, které se v jednom místě potkávají pod pravým úhlem (na pomyslné zeměkouli by se mohlo například jednat o část rovníku a poledníku). Na svislé ose pak ještě vyznačíme počáteční výšku kamene. Jeho světočáru tělesa jsme našli také jako geodetiku na povrchu pomocí proužku papíru. Proč jako geodetiku? Protože vše, co jsme si říkali u zakřivení ploch a prostoru platí stále, jen se posouváme o dimenzi výše. Geodetiku jsme zavedli fyzikálně jako trajektorii tělesa na zakřivené ploše, pokud na těleso nepůsobí žádné vnější síly. To znamená, že se pohybuje stále „rovně“, a jakákoli změna jeho pohybu je dána čistě geometrií dané plochy. V zakřiveném prostoru byly naše úvahy naprosto stejné, jen jsme se místo dvourozměrné zabývali třírozměrnou situací. Přechod z prostoru na prostoročas je podobný. V nezakřiveném prostoročase je „trajektorií“ tělesa přímka. V zakřiveném prostoročase je to zakřivený ekvivalent přímky – tedy geodetika. Zakřivení prostoročasu tedy způsobilo i zakřivení světočáry kamene. Výsledkem je, že se kámen dostává na nižší výšku. Začal sám od sebe padat a to pouze díky svému zakřivenému „pohybu“ v prostoročase. Žádné těleso ani částice totiž nemůže v prostoročase "stát na místě" už jen díky tomu, že existuje, a tím pádem pro něj plyne čas. Takže i když pak třeba stojí v klidu v prostoru, v prostoročase má nějakou trajektorii vždy.
Nyní je tedy náš popis gravitace, alespoň po kvalitativní stránce, kompletní. Pojďme si to tedy shrnout. V STR jsme zavedli prostoročas jako hypotetické propojení prostoru a času. Hlavním problémem a cílem našeho povídání o OTR je propojení speciální relativity a gravitace. Dospěli jsme k tomu, že gravitaci můžeme vysvětlit, pokud se na prostoročas v přítomnosti gravitace budeme dívat jako zakřivený, tedy aplikujeme na něj stejný matematický popis, jaký se používá například u zakřivených ploch. Rozdíl je v tom, že u ploch máme dvě prostorové souřadnice a v prostoročasu máme souřadnice čtyři – tři prostorové a jednu časovou. A protože to je poměrně velký koncepční krok, vzali jsme to postupně, ze dvou souřadnic jsme přešli na tři – k zakřivenému prostoru. Ukázalo se ale, že to nestačí. Museli jsme přidat právě i časovou složku, aby byl náš popis úplný. Tím jsme dospěli k již avizované základní myšlence obecné relativity: „Gravitace je zakřivení prostoročasu.“
Povrch koule podruhé
Posledních několik podkapitol jsme se seznamovali s hlavní myšlenkou obecné relativity kvalitativně. Naše úvahy byly co nejnázornější, ale přesto se jednalo jen o takové rozjímání nad problematikou. Nastal čas si přidat také trochu matematiky. Pokud totiž chceme něco i relativisticky spočítat, budeme muset chtě nechtě nahlédnout do matematického popisu křivosti. Samozřejmě nepůjdeme cestou plného matematického aparátu, který spadá už čistě do vysokoškolské matematiky. Pro naše účely si opět vystačíme s popisem co nejjednodušším a znovu půjdeme stejnou cestou jako dosud. Pokusíme se ukázat základní matematické zákonitosti používané u zakřivených ploch, které pak zobecníme na zakřivené prostory a prostoročas. Rozhodně z toho ale nemějte obavy a nevěšte hlavu, pokud vám to místy bude připadat těžké. Nemusíte nutně chápat vše, co si zde budeme říkat. Přece jen se jedná o dost abstraktní matematické myšlenky, které dávají zpočátku zabrat i vysokoškolákům. Matematikové nám tedy jistě prominou, když se oprostíme od přesných matematických definic a místo toho se pokusíme vše pojmout pokud možno co nejnázorněji. Berte tak následující podkapitoly jako snahu balancovat na hranici mezi názorností a rigorózním matematickým popisem. Uvidíme různá matematická tvrzení, jejichž odvození jsou povětšinou schována v rozbalovacích oknech pro zájemce. Rozhodně ale není nutné, abyste je znali. Jistě vám bude k užitku, pokud už někdy narazili na pojmy jako derivace nebo integrál (na které stejně ale většinou vyjma výběrového semináře z matematiky na střední škole už moc nenarazíme), ale rozhodně to není nezbytné. Nyní tedy zpět ke sféře…
Na první pohled se nám sféra může zdát jako trojrozměrný objekt. Rozprostírá se přeci tak nějak do všech směrů v prostoru. Když si umístíme sféru do kartézské souřadné soustavy, můžeme každému bodu sféry přiřadit tři souřadnice \([x,y,z]\) (obrázek 4.27 vlevo). Ve skutečnosti nám ale k úplnému popisu sféry stačí souřadnice dvě, podobně jako tomu je v rovině. Z definice se tedy nutně jedná o dvourozměrný objekt – plochu. Je to dáno tím, že kartézské souřadnice bodů na sféře nemohou být libovolné, jsou svázány dohromady vazebnou podmínkou \begin{equation*}\label{4.10}\tag{4.10} x^2+y^2+z^2=R^2, \end{equation*} kde \(x,y,z\) jsou souřadnice jednoho konkrétního bodu a \(R\) je poloměr sféry. Pro odvození podmínky \eqref{4.10} stačí, abyste si připomněli definici kartézských souřadnic z první části a následně trojrozměrnou Pythagorovu větu. Výsledek se dostaví okamžitě. Znamená to tedy, že pro určení bodu na sféře nemáme tři nezávislé souřadnice, ale pouze dvě. Třetí pak (až na znaménko) plyne z rovnice \eqref{4.10}. Také je z ní vidět, proč nemůžeme kouli reprezentovat jako 3D graf podobně jako jsme to udělali u hyperbolického paraboloidu. Když bychom totiž chtěli vyjádřit například souřadnici \(z\) pomocí ostatních, jako se to konvenčně dělává, dostáváme po odmocnění \(z=\pm\sqrt{R^2-x^2-y^2}\). Pro libovolný bod \([x,y]\) se souřadnicemi v intervalu \(\langle-R;R\rangle\) tedy máme dvě řešení odpovídající bodu nad a pod rovinou \(xy\), což odporuje nutné podmínce pro funkce, podle které musíme mít pro daný vstup pouze jeden výstup. Sféra se tedy nedá reprezentovat jako jeden 3D graf.
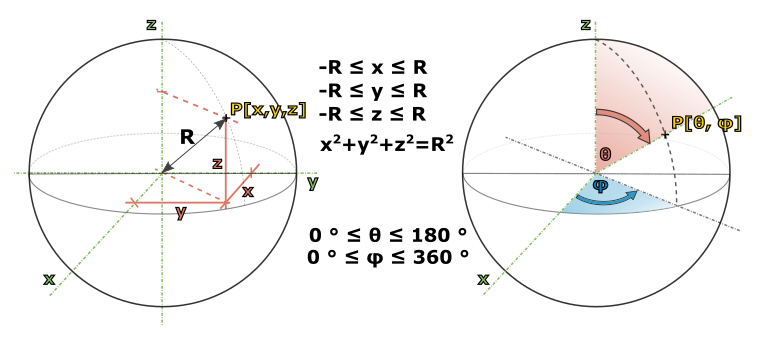
Obrázek 4.27 Vlevo: Tři kartézské souřadnice bodů na sféře nejsou nezávislé, jsou spojeny vazbou vyplývající z trojrozměrné Pythagorovy věty.
Vpravo: Ukázka zavedení úhlových souřadnic na sféře.
Jak už víme, geometrie na sféře a v rovině, byť obě vyžadují pro svůj popis dvě souřadnice, nejsou stejné. Již jsme se zmínili o komplikacích, které z toho plynou pro kartografy, a i my v dalším odvozování využijeme pro názornost naše zeměpisné znalosti, totiž zeměpisnou šířku a délku. Pomocí těchto dvou úhlů můžeme popsat polohu libovolného místa na Zemi (nadmořskou výšku v našich plošných úvahách vynecháme – bavíme se přeci jen o povrchu jednoduché sféry). Zeměpisná šířka má rozsah od \(90^°\) jižní zeměpisné šířky (jižní pól), přes \(0^°\) (rovník) až po \(90^°\) severní zeměpisné šířky (severní pól). Přesněji řečeno, jedná se o úhel mezi pomyslnou spojnicí popisovaného bodu se středem Země a rovníkem, kdy tento úhel bereme jako záporný pro jižní polokouli a kladný pro tu severní. Podobně zeměpisná délka jde od \(-180^°\) (západní směr) do \(180^°\) (východní směr), což je ve skutečnosti úhel odečítaný na rovníku mezi nultým poledníkem (který jak známo prochází anglickým Greenwichem) a poledníkem procházejícím bodem, který popisujeme. Například Praha se rozkládá přibližně na \(50^°5'14''\) severní šířky a \(14^°25'16''\) východní délky.
V matematice ale častěji zavádíme tyto sférické úhly trochu jinak. Nezabýváme-li se přímo geografií, jsou záporné hodnoty úhlů přece jen zbytečné. Usnadníme si tedy trochu život tím, že budeme měřit úhel \(\theta\) (zeměpisnou šířku) ne od rovníku, ale od severního pólu. Bude tak nabývat hodnot \(0^°\) až \(180^°\). Podobně budeme u zeměpisné šířky, tedy úhlu \(\varphi\), uvažovat rozsah \(0^°\) až \(360^°\) (obrázek 4.27 vpravo). Prakticky se pro nás téměř nic nezmění, stále si můžeme úhly představovat jako zeměpisnou šířku a délku, tuto informaci v sobě stále obsahují. Ale vzorce a odvození, která ještě potkáme, budou díky této volbě odpovídat vzorcům, které častěji potkáte i jinde v matematice. Většinou se prostě vyplatí držet se rozšířených (nejen matematických) konvencí.
Máme tedy dvě úhlové souřadnice pro popis polohy na této konkrétní zakřivené ploše. To, co ale typicky potřebujeme nejvíce, je umět určovat vzdálenosti. Jenže jak se to dělá u úhlových souřadnic?
Chceme-li v rovině určit vzdálenost dvou bodů pomocí jejich souřadnic, pomůže nám stará známá Pythagorova věta, jako jsme to viděli v první části. Ani s prostorovou vzdáleností nemáme problém, protože tam stačí do Pythagorovy věty přidat třetí souřadnici: \begin{equation*}\label{4.11}\tag{4.11} (\Delta{}s_\text{k})^2=(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2 . \end{equation*} V rovnici \eqref{4.11} jsme označili \(Δs_\text{k}\) jako kartézskou vzdálenost (někdy se nazývá také eukleidovská, protože Pythagorova věta, jak ji typicky známe, je platná jen v eukleidovské rovině, potažmo prostoru). Na sféře nám ale tato rovnice nepomůže, protože automaticky určuje vzdálenost v prostoru – tedy skrz kouli. A to, jak už víme, je pro nás nedovolený postup. Musíme tedy využít souřadnice, které respektují povrch koule, což jsou právě například úhlové souřadnice \(\theta\) a \(\varphi\).
Předně si musíme vzpomenout, jak měříme vzdálenost v kartézské rovině. Tradičně volíme dvě na sebe kolmé osy a každá rovnoběžka s osou je poté přímka o konstantní souřadnici (například libovolná rovnoběžka s osou x vyznačuje konkrétní neměnící se hodnotu souřadnice y kdekoli na této přímce). Jednotlivé body jsou pak průsečíky rovnoběžek odpovídajících konkrétním souřadnicím (obrázek 4.28 vlevo), a vzdálenost mezi nimi určujeme pomocí příslušných rozdílů souřadnic a Pythagorovy věty (vizte obrázek 1.6 v první části). Podobně i na povrchu koule můžeme určit křivky o konstantní hodnotě jedné souřadnice (obrázek uprostřed a vpravo), které jsou na sebe kolmé v každém bodě. Jsou to samozřejmě naše staré známé poledníky a rovnoběžky.
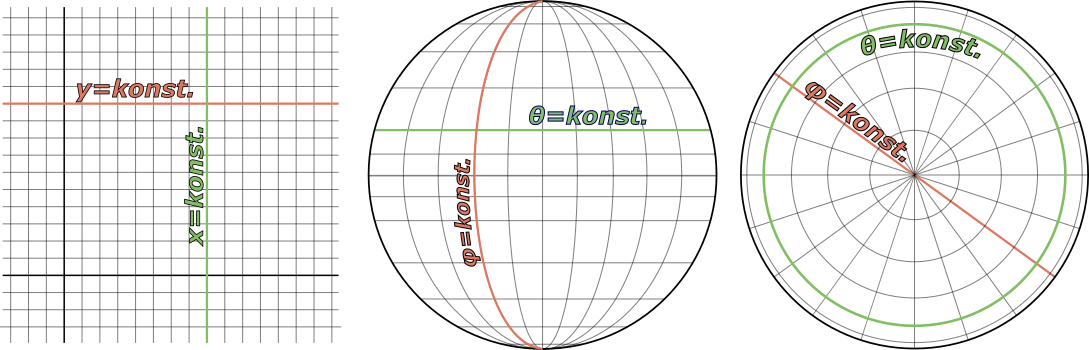
Obrázek 4.28 Vlevo:V kartézské souřadné soustavě je každý bod určen jako průsečík rovnoběžek s osami o příslušné konstantní souřadnici.
Uprostřed a vpravo: Křivky konstantní hodnoty souřadnic \(\theta\) a \(\varphi\) protínající se pod pravým úhlem, pohled „zboku a shora“. Kdekoli mimo póly jsou tyto křivky analogií ke kartézským osám a rovnoběžným přímkám, pomocí kterých určujeme vzdálenosti. Na pólech jsou tyto úhlové souřadnice singulární, tedy neurčují daný bod jednoznačně (jaký úhel \(\varphi\) odpovídá pólům?).
Na obrázku 4.29 vlevo vidíme jednoduchý příklad dvou bodů na stejné souřadnici \(\varphi\). Pro sférickou vzdálenost mezi body, což je délka příslušného oblouku, který je spojuje, platí \(\Delta{}s_{sf}=\Delta\theta R\). Platnost tohoto vzorečku si uvědomíme snadno, protože obvod celé příslušné kružnice by byl \(2\pi R\), polovina kružnice by byla \(\pi R\) apod. Délka oblouku je tedy vždy jeho poloměr vynásobený úhlem, který oblouk vytýká. Samozřejmě úhel musí být v radiánech, aby výpočet fungoval. Se stupni bychom zde nepochodili. Například už proto, že kružnice o poloměru \(1\:\text{m}\) zcela jistě nemá obvod \(360\:\text{m}\). Příslušný úhel oblouku v tomto případě najdeme snadno jako rozdíl "zeměpisných šířek" bodů \(A\) a \(B\), tj. \(\Delta\theta=|\theta_A-\theta_B|\) (absolutní hodnotu jsme přidali, bychom se nemuseli starat o to, která ze souřadnic je větší).
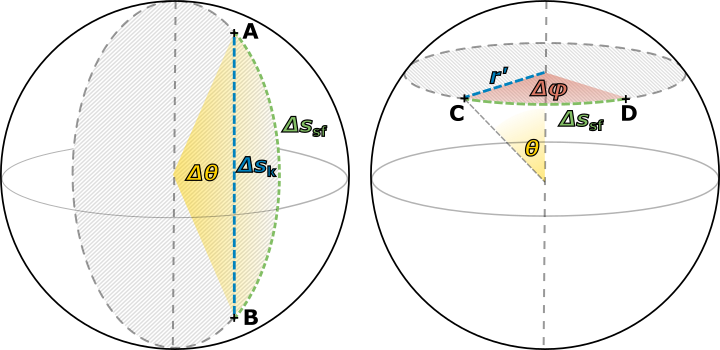
Obrázek 4.29 Trojrozměrná kartézská vzdálenost dvou bodů umístěných na sféře \(\Delta{}s_\text{k}\) vypočítaná vzorcem \eqref{4.11} nerespektuje zadanou plochu. Při pohybu na povrchu koule se nemůžeme provrtat napříč jejím povrchem, proto musíme najít způsob, jak spočítat sférickou vzdálenost \(\Delta{}s_{\text{sf}}\). Na obrázku vidíme sférickou vzdálenost pro dva body na stejném poledníku (vlevo) a pro dva body na stejné rovnoběžce (vpravo).
V případě vzdálenosti mezi dvěma body na stejné rovnoběžce je situace o trochu složitější. Body mají tentokrát stejnou úhlovou souřadnici \(\theta\) a liší se ve \(\varphi\) (obrázek 4.29 vpravo). Opět využijeme souřadnicového rozdílu \(\Delta\varphi=|\varphi_C-\varphi_D|\), nicméně poloměr příslušné rovnoběžky spojující body \(C\) a \(D\) není totožný s poloměrem sféry. Podle odvození vzorce \eqref{4.3} (a zejména přiloženého obrázku) můžeme ale tento poloměr spočítat jednoduše jako \(r^\prime=R\sin{\theta}\), kde \(\theta\) je samozřejmě úhel odpovídající dané rovnoběžce. Délka oblouku mezi body \(C\) a \(D\) tedy bude \(\Delta{}s_{\text{sf}}=r^\prime\Delta\varphi=R\sin{\theta}\Delta{\varphi}\) (připomeňme ale, že zatímco u části poledníku se jednalo o skutečnou vzdálenost mezi body \(A\) a \(B\), část rovnoběžky není nejkratší vzdálenost mezi body \(C\) a \(D\), protože není částí hlavní kružnice, pouze délkou oblouku podél osy konstantní souřadnice, kterou dokážeme snadno najít). V situaci, kdy oba body leží na jednom poledníku či rovnoběžce, nám k výpočtu oblouku stačila jednoduchá úvaha. Jak to ale bude v obecném případě, tedy jako na obrázku 4.30?
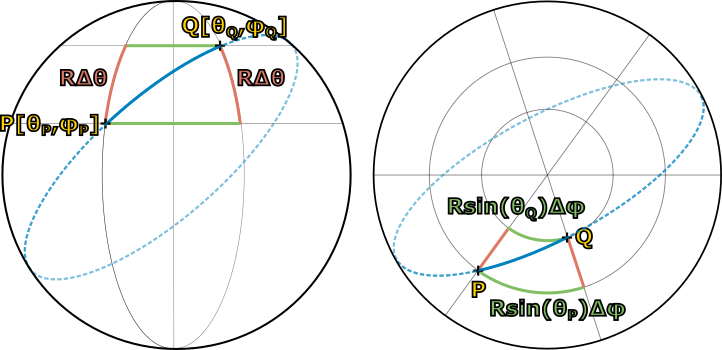
Obrázek 4.30 Dva vybrané body na sféře, jejich vzájemná vzdálenost a příslušné oblouky odpovídající rozdílům v úhlových souřadnicích. Zjevně „poledníková“ vzdálenost nezávisí na volbě poledníku, ale u rovnoběžek to už neplatí.
Obrázek 4.31 Měření vzdáleností na nafukovacím míči.
Po všem, co jsme si řekli o sférické geometrii, nás asi nepřekvapí, že s přímou aplikací Pythagorovy věty na příslušné oblouky (byť tvořící pravý úhel) moc daleko nedojdeme. Koneckonců, platnost Pythagorovy věty je přímým důsledkem axiomů eukleidovské geometrie, která na sféře neplatí. Můžeme si to dokonce vyzkoušet přímo pomocí reálného modelu. Vezměme si k ruce míč či jiný model koule, který jsme využívali v podkapitole „Povrch koule poprvé“. Velmi výhodné je použít glóbus, protože jsou na něm rovnoběžky a poledníky rovnou nakresleny (obrázek 4.31). Pokud glóbus k dispozici nemáme, nemusíme nutně črtat celou souřadnicovou síť, stačí jen její část. Na našem modelu si vždy vybereme dva body a přímo změříme jejich vzdálenost například pomocí provázku. Zároveň změříme délky příslušných oblouků na konstantní zeměpisné šířce a délce, jako je vyznačeno na obrázku. Pro jednoduchost jsme vybrali vždy dvojice bodů, kdy jeden leží na rovníku (\(\theta=90^°\)) a druhý na nultém poledníku (\(\varphi=0^°\)). Abychom byli precizní, budeme měřit příslušné vzdálenosti na obou rovnoběžkách, jak je vyznačeno v obrázku. V tabulce 4.1 máme shrnutí, jak se skutečná naměřená vzdálenost mezi body \(\Delta s_{\text{měř}}\) liší od té, kterou dostaneme (samozřejmě neoprávněným) přímým použitím Pythagorovy věty:
| Tabulka 4.1 Shrnutí výsledků měření vzdáleností na míči. | ||||
|---|---|---|---|---|
| \(\boldsymbol{[\theta_A,\varphi_A]}\) | \(\boldsymbol{[\theta_B,\varphi_B]}\) | \(\boldsymbol{\epsilon_{r1}/\%}\) | \(\boldsymbol{\epsilon_{r2}/\%}\) | |
| 1. | \([90^°,10^°]\) | \([80^°,0^°]\) | \(0{,}76\) | \(1{,}99\) |
| 2. | \([90^°,20^°]\) | \([70^°,0^°]\) | \(1{,}72\) | \(1{,}33\) |
| 3. | \([90^°,30^°]\) | \([60^°,0^°]\) | \(2{,}37\) | \(1{,}25\) |
| 4. | \([90^°,40^°]\) | \([50^°,0^°]\) | \(3{,}91\) | \(3{,}41\) |
| 5. | \([90^°,50^°]\) | \([40^°,0^°]\) | \(5{,}57\) | \(7{,}95\) |
| 6. | \([90^°,60^°]\) | \([30^°,0^°]\) | \(10{,}02\) | \(14{,}10\) |
Detailnější popis měření a naměřených hodnot si můžete rozbalit níže. Pro nás jsou nyní důležité poslední dva sloupce tabulky. Ukazují relativní odchylku skutečné naměřené vzdálenosti od použití Pythagorovy věty pro severnější a jižnější cestu (blíže komentováno v rozbalovacím popisu níže). Z uvedených čísel vidíme, že čím jsou vybrané body blíže k sobě, tím se relativní chyba zmenšuje. Naše zjištění samozřejmě není tak moc překvapivé, když si uvědomíme, že ačkoli je například povrch naší planety přibližně sférický, přesto na něm Pythagorovu větu (či obecně eukleidovskou geometrii) běžně používáme. Například ve stavebnictví tvoří naprosto zásadní pomůcku, jak vytvářet pravé úhly. Souvisí to samozřejmě s velikostí naší planety. Pokud se oprostíme od nerovností zemského povrchu, je sice, jak už víme, jakákoli „rovná“ čára na povrchu Země ve skutečnosti částí kružnice, ale pro dostatečně malé vzdálenosti ji jen velmi stěží odlišíme od úsečky. Jak malé? Jednoduchým výpočtem bychom zjistili, že pokud bychom si jako hranici přesnosti stanovili \(0{,}1\%\), mohli bychom za rovné považovat čáry dlouhé téměř \(740\:\text{km}\)! Pro srovnání, tato hodnota odpovídá silniční vzdálenosti z Prahy do Lucemburska. A i v tomto případě bychom se dopustili chyby jen necelý km. Tohle je přesně ten důvod, proč se nám Země zdá placatá a proč si to bohužel i v dnešní době někteří lidé stále myslí. Každá koule, pokud budeme pracovat s dostatečně malým úsekem, se bude jevit jako placatá a naše planeta je v lidských měřítkách opravdu velká.
Princip měření je následující. Pro vybrané dvojice bodů změříme vždy délky příslušných oblouků \(\Delta s_{\text{pol}}\) a \(\Delta s_{\text{rov}}\), které oddělují body na jedné konstantní souřadnici. Pro rovnoběžkovou vzdálenost máme dvě možnosti – „severnější“ \(\Delta s_{\text{rov1}}\) a „jižnější“ \(\Delta s_{\text{rov2}}\). V tabulce 4.1a máme shrnutí, jak se skutečná naměřená vzdálenost mezi body \(\Delta s_{\text{měř}}\) liší od té, kterou dostaneme (samozřejmě neoprávněným) přímým použitím Pythagorovy věty na naměřené délky oblouků podle \begin{equation*} \Delta s_{Pyt1,2}=\sqrt{(\Delta s_{pol})^2+(\Delta s_{rov1,2})^2}. \end{equation*} Ve vztahu si vždy vybíráme jen jednu hodnotu indexů, takže \(\Delta s_{\text{Pyt1}}\) se počítá pomocí \(\Delta s_{\text{rov1}}\) atd. Na konci tabulky 4.1a je spočítána také relativní odchylka pro oba případy. Nejdůležitější na celém tomto pokusu je, že čím blíže sobě dva zvolené body jsou, tím jsou výsledky získané prostým dosazením do Pythagorovy věty přesnější.
| Tabulka 4.1a Měření vzdálenosti bezi vybranými body na nafukovacím míči z obrázku 4.30. Významy veličin \(\Delta{}s_{pol}\),\(\Delta{}s_{rov}\) a \(\Delta{}s_{měř}\) jsou patrné z obrázku. Všechny naměřené délky a výsledky byly zaokrouhleny na celé mm. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(\boldsymbol{[\theta_A,\varphi_A]}\) | \(\boldsymbol{[\theta_B,\varphi_B]}\) | \(\boldsymbol{\Delta{}s_{pol}}\) | \(\boldsymbol{\Delta{}s_{rov1}}\) | \(\boldsymbol{\Delta{}s_{rov2}}\) | \(\boldsymbol{\Delta{}s_{Pyt1}}\) | \(\boldsymbol{\Delta{}s_{Pyt2}}\) | \(\boldsymbol{\Delta{}s_{měř}}\) | \(\boldsymbol{\epsilon_{r1}/\%}\) | \(\boldsymbol{\epsilon_{r2}/\%}\) | |
| 1. | \([90^°,10^°]\) | \([80^°,0^°]\) | \(40\) | \(40\) | \(39\) | \(57\) | \(56\) | \(57\) | \(0{,}76^*\) | \(1{,}99\) |
| 2. | \([90^°,20^°]\) | \([70^°,0^°]\) | \(82\) | \(82\) | \(77\) | \(116\) | \(112\) | \(114\) | \(1{,}72\) | \(1{,}33\) |
| 3. | \([90^°,30^°]\) | \([60^°,0^°]\) | \(124\) | \(125\) | \(115\) | \(176\) | \(170\) | \(112\) | \(2{,}37\) | \(1{,}25\) |
| 4. | \([90^°,40^°]\) | \([50^°,0^°]\) | \(165\) | \(170\) | \(140\) | \(237\) | \(220\) | \(228\) | \(3{,}91\) | \(3{,}41\) |
| 5. | \([90^°,50^°]\) | \([40^°,0^°]\) | \(207\) | \(211\) | \(148\) | \(296\) | \(258\) | \(280\) | \(5{,}57\) | \(7{,}95\) |
| 6. | \([90^°,60^°]\) | \([30^°,0^°]\) | \(249\) | \(252\) | \(114\) | \(354\) | \(277\) | \(322\) | \(10{,}02\) | \(14{,}10\) |
Připusťme tedy nyní, že pro dostatečně blízké body můžeme na sféře Pythagorovu větu opravdu použít. S použitím délek oblouků vytyčených na rovnoběžkách a polednících tak dostáváme pro vzdálenost dvou blízkých bodů na sféře o poloměru \(R\) \begin{equation*}\label{4.12}\tag{4.12} (\Delta{}s)^2 \dot{=}(R\Delta\theta)^2+(R\sin{\theta}\Delta\varphi)^2 \qquad \text{(blízké body).} \end{equation*} Tento vztah je, striktně vzato, nejednoznačný, protože zde neurčujeme, které θ se používá. Protože jsme ale viděli, že se zmenšující se vzdáleností bodů se k sobě délky „horní“ a „dolní“ cesty blížily, můžeme v našem přiblížení blízkých bodů vzít kteroukoli ze dvou hodnot, případně jejich průměrnou hodnotu, tj. \(\theta=(\theta_P+\theta_Q)/2\). Abychom nemuseli neustále používat znaménka přibližně, zaveďme si konvenci značení pro „dostatečně malé rozdíly“. Namísto konečné změny \(\Delta\) budeme psát \(\text{d}\), tedy například \(\text{d}s\). Máme tím na mysli, že daná změna je dostatečně malá na to, abychom mohli na dané křivé ploše použít jednoduchou Pythagorovu větu. Rovnice \eqref{4.12} pak bude vypadat \begin{equation*}\label{4.13}\tag{4.13} (\text{d}s)^2=R^2(\text{d}θ)^2+R^2\sin^2{\theta}(d\varphi)^2. \end{equation*}
Poznámka 4.7
V matematice se taková „dostatečně malá“ změna nazývá diferenciál a mluví se o ní jako o nekonečně malé nebo také infinitezimální. To je na první pohled samozřejmě velmi matoucí a vágní označení. Jak by mohla být vzájemná vzdálenost dvou nekonečně blízkých bodů něco jiného než… co vlastně? Nula? Nekonečně málo? Podobné otázky nás jen matou. Vězte, že existují přesné definice a matematické operace zabývající se nekonečně malými veličinami, ale my je zde zavádět nebudeme. A i když budeme často pro stručnost mluvit o například nekonečně malé vzdálenosti, doporučujeme se vždy přidržet praktické představy - nekonečně malé znamená dostatečně malé na to, aby nějaké naše dané zjednodušení fungovalo.
Možná se vám tento postup zdá jako podvod, případně, že má silně omezenou platností. Na jednu stranu jsme získali velmi jednoduchý vztah, na druhou ho nemůžeme použít na libovolně velké vzdálenosti. Spočítat na sféře konečnou vzdálenost mezi dvěma obecně umístěnými body přesně je poměrně komplikované (a u složitějších ploch už to nemusí jít vůbec). Co bychom mohli udělat, je rozdělit si daný oblouk na řadu krátkých úseků a na každý použít vzorec \eqref{4.13}. Samozřejmě čím více úseků použijeme, tím menší každý z nich bude a tím přesnější bude i náš výsledek. Je to podobné, jako bychom u pravidelného mnohoúhelníku zvětšovali počet vrcholů. Od určitého počtu bychom již nedokázali rozeznat mnohoúhelník od kružnice. Názorně to vidíme na obrázku 4.32, kde pro jednoduchost a názornost nahrazujeme čtvrtinu kružnice o jednotkovém poloměru lomenou čarou s různými počty segmentů. Vlevo vidíme, že pro deset úseků již v tomto případě skoro nerozeznáme zelenou lomenou čáru od čárkovaného oblouku. Vpravo pak máme srovnání délky lomené čáry pro různé počty segmentů s očekávanou hodnotou délky čtvrtiny kružnice o jednotkovém poloměru \(\pi/2\). Zjevně vidíme nepřekvapivý výsledek, že s vyšším počtem úseků se blížíme k přesnému výsledku, nicméně pro žádné konečné N ho nemůžeme dosáhnout. Tímto postupem můžeme maximálně chybu tohoto postupu libovolně snížit (například zajímá-li nás délka s přesností na celé metry, lze vždy nalézt takové dělení, aby chyba byla menší než půl metru).
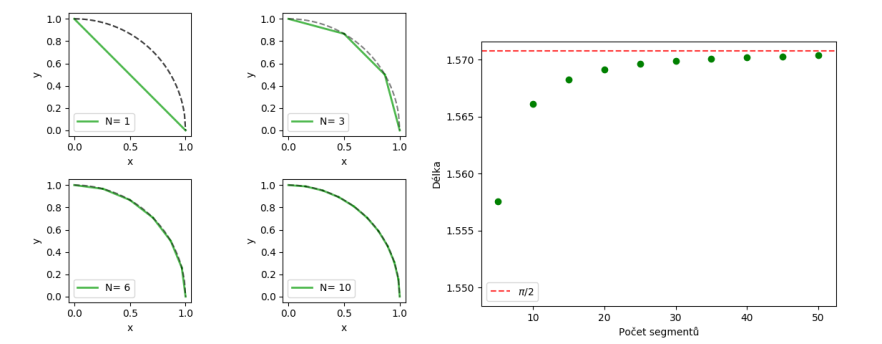
Obrázek 4.32 Vlevo: Vybrané ukázky nahrazení čtvrtkružnice o jednotkovém poloměru lomenou čárou o daném počtu segmentů.
Vpravo: Graf závislosti délky lomené čáry na počtu segmentů \((N=5,10,15,\dots,50)\) porovnaný se správnou hodnotou \(\pi/2=1,57079\dots\)
Aby byl náš výpočet zcela přesný, museli bychom oblouk rozdělit teoreticky na nekonečně mnoho dílů, které budou tím pádem nekonečně malé. A zde se dostáváme k základní myšlence části matematiky nazývané diferenciální a integrální počet, se kterou se setkáváme pořádně až na technicky či přírodovědně zaměřených vysokých školách (případně, jak už bylo řečeno, první setkání může proběhnout na výběrových matematických seminářích na střední škole). Na první pohled může být překvapivé, že je něco takového možné, a že to ještě ke všemu funguje, pracovat s nekonečně malými veličinami a pak ještě nekonečně mnoho těch nekonečně malých kousků posčítat. V tuto chvíli by pro nás bylo příliš zdlouhavé vybudovat potřebnou matematiku derivací a integrálů od začátku, takže (přesně v duchu tohoto textu) ti z vás, kteří už o podobné pojmy někdy zavadili, se mohou na konkrétní příklad výpočtu podívat níže. Pokud vám tyto pojmy nic neříkají, můžete se ze zájmu podívat taky, ale pokud něčemu nebudete rozumět, neklesejte na mysli, jsou to jenom technické detaily. Soustřeďte se místo toho na podstatu věci. Geometrie zakřivených ploch je z matematického hlediska lokální. To znamená, že odvozuje jednoduché vztahy platné jen na nekonečně malé části plochy (prakticky řečeno, libovolně zakřivená plocha je podobná rovině, pokud se soustředíme na dostatečně malou oblast). Zde totiž můžeme použít starou známou eukleidovskou geometrii, například a zejména Pythagorovu větu. Cenou za toto zjednodušení ale je, že následně musíme tyto nekonečně malé kousky „lepit“ dohromady pomocí pokročilejší matematiky.
V našem příkladu nahrazujeme čtvrtkružnici lomenou čarou, jejíž délku spočítáme jednoduše jako součet délek jednotlivých částí. Známe-li souřadnice jednotlivých bodů, můžeme snadno najít jejich vzdálenost pomocí rozdílů souřadnic a Pythagorovy věty, jak je patrné z obrázku. Délka lomené čáry tedy pak bude \begin{equation*} \sum_{i=1}^N\sqrt{(\Delta{}x_i)^2+(\Delta{}y_i)^2}, \end{equation*} kde sčítáme přes všechny dílky. Jak jsme viděli, čím bude \(N\) větší číslo, tím bude hledaná délka blíže přesné hodnotě \(\pi/2\). Abychom ale dostali zcela přesný výsledek, musíme teoreticky použít nekonečně mnoho úseků, které se tím pádem stávají nekonečně malými. V takovém případě místo sumy (tj. konečného součtu) musíme použít nekonečný součet neboli integrál. Upravíme-li sumu vytknutím \(\Delta{}x\), můžeme následně přejít limitně k integraci \begin{equation*} \sum_{i=1}^N\sqrt{(\Delta{}x_i)^2+(\Delta{}y_i)^2}=\sum_{i=1}^N\sqrt{1+\left(\frac{\Delta{}y_i}{\Delta{}x_i}\right)^2}\Delta x_i\xrightarrow{N\to\infty}\int^{x_2}_{x_1}\sqrt{1+(y^\prime)^2}\text{d}x, \end{equation*} kde jsme využili definice derivace jako právě limity podílu souřadnic \begin{equation*} y^\prime(x)=\lim_{\Delta{}x\to 0}\frac{\Delta y}{\Delta x}. \end{equation*} Z podstaty věci by mělo být zřejmé, že jak jdeme s počtem úseků \(N\) do nekonečna, tak se nutně zmenšuje rozdíl souřadnic vedlejších bodů k nule. Vlastně jsme právě odvodili vzorec pro výpočet délky libovolné křivky, která je grafem nějaké funkce \(y(x)\). Snadno si můžete ověřit, že v našem případě jednotkové kružnice je takovou funkcí \(y(x)=\sqrt{1-x^2}\) a pohybujeme se na intervalu \(x\in\langle0;1\rangle\). K výpočtu potřebujeme znát derivaci této funkce, což je \begin{equation*} y^\prime(x)=\left(\sqrt{1-x^2}\right)^\prime=\frac{\frac{1}{2}}{\sqrt{1-x^2}}\left(1-x^2\right)^\prime=\frac{\frac{1}{2}}{\sqrt{1-x^2}}\left(-2x\right)=\frac{-x}{\sqrt{1-x^2}}. \end{equation*} Ve výpočtu jsme využili pravidlo pro derivaci složené funkce. Přesnou délku oblouku pak dostaneme jako \begin{equation*} \int_0^1\sqrt{1+(y^\prime)^2}\text{d}x=\int_0^1\sqrt{1+\frac{x^2}{1-x^2}}\text{d}x=\int_0^1\sqrt{\frac{1}{1-x^2}}\text{d}x=\left[\operatorname{arsin}(x)\right]_0^1=\frac{\pi}{2}-0=\frac{π}{2}. \end{equation*} Ještě jednou připomeňme, že pokud vám nějaký krok nebo i celý tento výpočet nedává smysl, netrapte se tím. Nebudeme tyto znalosti nutně potřebovat.
Metrika je základ
Vztah \eqref{4.12} nám prakticky říká dvě věci. Za prvé, což nás vcelku nepřekvapuje, že Pythagorova věta ve své klasické formě na sféře nefunguje. Za druhé, že její „funkčnost“ můžeme zachránit, pokud se budeme věnovat dostatečně malým situacím (vzpomínáte na lokální inerciální systémy?) a zároveň pokud budeme používat souřadnice správně popisující danou plochu. Druhý požadavek je neméně důležitý; viděli jsme, že kartézské souřadnice by na celé sféře nefungovaly. Důsledkem ale je, že se nám v této „zobecněné Pythagorově větě“ objevily koeficienty u přírůstků souřadnic. A podobně, jako jsme rovnici \eqref{4.12} odvodili pro sféru, bychom to mohli udělat pro libovolnou jinou plochu (a níže si ukážeme několik dalších příkladů). Ukazuje se, že tvar tohoto vztahu v sobě obsahuje v podstatě vše důležité o vnitřní geometrii dané plochy. Má proto taky svůj vlastní název – metrika. Jedná se v podstatě o předpis, jak spočítat v daných souřadnicích respektujících geometrii plochy vzdálenost dvou nekonečně blízkých bodů. Nezapomínejme ale, že prakticky vždy je pro nás důležitá konečná vzdálenost, kterou počítáme „slepením“ těchto nekonečně malých kousků dohromady (tj. integrací). A ačkoli se jedná o technicky komplikovaný matematický proces, kterému se zde nevěnujeme, je snad vcelku jasné, že konkrétní forma těchto „malých kousků“, tzn. tvar metriky, je důležitá, protože ovlivní celkový výsledek.
| Tabulka 4.2 Vzájemné vzdálenosti čtyř bodů v milimetrech. | ||||
|---|---|---|---|---|
| \(\boldsymbol{K}\) | \(\boldsymbol{L}\) | \(\boldsymbol{M}\) | \(\boldsymbol{N}\) | |
| \(\boldsymbol{K}\) | \(-\) | \(40\) | \(25\) | \(35\) |
| \(\boldsymbol{L}\) | \(-\) | \(30\) | \(50\) | |
| \(\boldsymbol{M}\) | \(-\) | \(30\) | ||
| \(\boldsymbol{N}\) | \(-\) | |||
Není jednoduché ukázat, že metrika v sobě opravdu obsahuje vše důležité o vnitřní geometrii plochy. Zkusme si to alespoň, jak je naším zvykem, rozmyslet na jednoduchém příkladu. Metrika nám umožňuje počítat vzdálenosti v dané ploše mezi libovolnými dvěma body. Pokud bychom chtěli například zreprodukovat tvar nějaké komplikované plochy, mohli bychom si na ploše vyznačit zvolené množství bodů a změřit jejich vzájemné vzdálenosti. Výsledkem by byla tabulka vzdáleností pro každou dvojici. Je asi zřejmé, že čím přesněji chceme danou plochu zreprodukovat, tím více bodů na to potřebujeme, ale o to zdlouhavější celý proces bude. Abychom se zbytečně nezahlcovali, ukažme si příklad čtyř bodů \(K,L,M,N\), jejichž vzájemné vzdálenosti jsou v tabulce 4.2.
Diagonála je pochopitelně prázdná, protože neuvažujeme vzdálenosti bodu od sebe samotného, respektive psát tam nuly by bylo zbytečné. Zároveň nepotřebujeme vyplňovat políčka pod diagonálou, protože se jedná o stejné hodnoty jako nad ní. Pro čtyři body tedy máme šest hodnot vzájemných vzdáleností. Sami si můžete rozmyslet, že pro \(n\) bodů bychom měli \((n^2-n)/2\) hodnot (stačí se zadívat na tabulku). Nyní si zkusme odpovědět na otázku: jsou všechny čtyři body v jedné rovině? Určitě existují různé způsoby, jak to zjistit. Nejsnazší to ale bude prostě vyzkoušet, tj. postupně umisťovat body v souladu se zadanými vzdálenostmi, jak to vidíme na obrázku 4.33.
Obrázek 4.33 Postupné vykreslování bodů podle jejich zadaných vzájemných vzdáleností.
- Začneme bodem \(K\), který umístíme naprosto libovolně v naší rovině (papíru). Bod \(L\) můžeme umístit libovolně na kružnici se středem v bodě \(K\) a poloměrem \(40\:\text{mm}\), tím splníme podmínku vzdálenosti \(|KL|=40\:\text{mm}\).
- Abychom našli bod \(M\), postup zopakujeme pro dvě kružnice se středy v bodech \(K\) a \(L\) a příslušných poloměrech. Kružnice se protínají ve dvou bodech. My si vybereme jeden z nich a je jedno který, protože dvě příslušná řešení jsou navzájem osově symetrická, takže se z našeho pohledu prakticky neliší. Zatím jsme nemuseli pracovat prostorově (tj. místo kružnic použít sféry), protože už ze středoškolské geometrie víme, že libovolnými třemi body v prostoru, neleží-li na stejné přímce, lze jednoznačně proložit rovinu.
- Když ale zkusíme do roviny umístit bod \(N\), najednou zjistíme, že není možné najít v dané rovině bod, který by byl vzdálený \(35\:\text{mm}\) od bodu \(K\) a zároveň \(50\:\text{mm}\) od bodu \(L\) a zároveň \(30\:\text{mm}\) od bodu \(M\). Kružnice se neprotnou v žádném bodě všechny najednou. Bod \(N\) tedy nutně leží mimo rovinu určenou body \(K,L,M\).
- Abychom našli bod \(N\), musíme tedy místo kružnic použít sféry (které na obrázku pro přehlednost nevykreslujeme), princip je ale podobný jako u kružnic. Sféry by se nám protnuly opět ve dvou bodech, „nad“ a „pod“ rovinou, stačí si vybrat jeden z nich, podobně jako u bodu \(M\).
Ať už tedy body \(K,L,M\) a \(N\) leží na jakékoli ploše, rozhodně to není rovina. Samozřejmě, pokud bychom tuto plochu chtěli nějak přesněji zreprodukovat, potřebovali bychom více informací, tzn. více bodů. To už dělat nebudeme. Chtěli jsme pouze ukázat, že ze znalosti vzájemných vzdáleností bodů je v principu možné zreprodukovat jakoukoli plochu libovolně přesně. A protože metrika dané plochy je obecně nástrojem pro výpočet vzdáleností mezi body na této ploše, obsahuje tedy v sobě všechny potřebné informace o její vnitřní geometrii.
Podívejme se nyní na několik důležitých příkladů metrik. Například metriku roviny již vlastně známe. Máme-li rovinu popsanou dvěma na sebe kolmými souřadnicemi \(x\) a \(y\), bude kvadrát vzdálenosti libovolných dvou bodů jednoduše \((\Delta s)^2=(\Delta x)^2+(\Delta y)^2\) a protože jsme v rovině, tento vzorec platí i pro libovolně blízké body (jinak řečeno Pythagorova věta platí v rovině bez ohledu na vzdálenost dané dvojice bodů). Dostáváme tedy metriku roviny jako \begin{equation*}\label{4.14}\tag{4.14} (\text{d} s)^2=(\text{d} x)^2+(\text{d} y)^2, \end{equation*} tj. druhou mocninu vzdálenosti dvou nekonečně blízkých bodů na druhou je malý kousek ve směru \(x\) na druhou plus malý kousek ve směru \(y\) na druhou. Zde žádné koeficienty u přírůstků souřadnice nemáme, respektive příslušné koeficienty jsou jedničky, tedy všude stejné konstanty. Na sféře tomu tak nebylo: \((\text{d} s)^2=R^2(\text{d}\theta)^2+R^2\sin^2{\theta}(\text{d}\varphi)^2\) v sobě obsahuje \(\sin^2\theta\), který je v různých bodech sféry různý. V případě sféry bychom nemohli použít například \((\text{d} s)^2=(\text{d}\theta)^2+(\text{d}\varphi)^2\), zejména proto, že na levé straně máme druhou mocninu vzdálenosti a na pravé druhé mocniny úhlu, nesedí nám zde jednotky. Ale ani kdybychom ponechali \((\text{d} s)^2=R^2(\text{d}\theta)^2+R^2 (\text{d}\varphi)^2\), což už sedí jednotkově, tak by to nefungovalo, protože bychom dostávali nesprávné výsledky, například už jen v případě, kdy budou dva body ležet na stejné rovnoběžce (jako na obrázku 4.29 vpravo).
Obrázek 4.34 Vzdálenost dvou velmi blízkých bodů v rovině popsané souřadnicemi, jejichž osy svírají úhel menší než \(90°\).
Viděli jsme, že pro různě zakřivené plochy dostáváme různé tvary metriky. Naopak to ale platit nemusí. Je možné, že dvě na první pohled různé metriky mohou popisovat stejnou plochu. Podívejme se na příklad roviny, kterou popíšeme ne pomocí dvou kolmých os, ale necháme je svírat nějaký daný úhel \(\alpha\) (obrázek 4.34). Označme tyto souřadnice \(x^\prime\) a \(y^\prime\). Vybereme-li si libovolné dva body \(A\) a \(B\), můžeme najít jejich vzdálenost vyjádřenou rozdíly obou souřadnic. Připomeňme, že například příslušnou souřadnici \(x^\prime\) bodu \(A\) najdeme vedením rovnoběžky s osou \(y^\prime\) tímto bodem a odečtením souřadnice průsečíku s osou \(x^\prime\). Rozdíly souřadnic jsou potom vzdálenosti příslušných průsečíků na osách. Protože se nacházíme v rovině, je prakticky jedno, jestli pracujeme s konečnými vzdálenostmi \(\Delta s\) nebo s nekonečně malými \(\text{d}s\). Aby ale byly naše vzorce v souladu s \eqref{4.14}, budeme uvažovat infinitezimálně blízké body. Podle obrázku 4.34 najdeme kvadrát \(\text{d}s\) pomocí kosinové věty (jejímž speciálním případem je i Pythagorova věta pro \(\beta=90°\)). Podle ní platí \begin{equation*} (\text{d}s)^2=(\text{d}x^\prime)^2+(\text{d}y^\prime)^2-2\text{d}x^\prime\text{d}y^\prime\cos\beta. \end{equation*} Protože se součet vnitřních úhlů ve čtyřúhelníku musí rovnat \(360°\), platí \(2\alpha+2\beta=360°\), z čehož plyne \(\beta=180°-\alpha\). Nakonec si stačí uvědomit, že \(\cos(180°-\alpha)=-\cos(-\alpha)=-\cos(\alpha)\) (ponecháme na čtenáři, aby si tuto poslední úpravu dokázal sám, buďto pomocí známých vzorců pro kosinus součtu úhlů nebo vykreslením funkcí v grafu). Celkem tedy dostáváme \begin{equation*}\label{4.15}\tag{4.15} (\text{d}s)^2=(\text{d}x^\prime)^2+(\text{d}y^\prime)^2+2\text{d}x^\prime\text{d}y^\prime\cos\alpha. \end{equation*} Takže pro stejnou rovinu jsme v nových souřadnicích dostali trochu odlišnou metriku. Koeficienty u kvadrátů přírůstků souřadnice jsou sice stále jedničky, ale vyšel nám nový člen obsahující už ne kvadráty, ale součin přírůstků dvou různých souřadnic. Tento tzv. křížový člen se typicky vyskytuje u souřadnic, které na sebe nejsou kolmé, což je přesně náš případ. Klasické kartézské souřadnice \(x\) a \(y\) v rovině nebo i úhlové souřadnice \(\theta\) a \(\varphi\) na kouli na sebe kolmé jsou, proto jsme zatím žádné křížové členy nepotkali.
Dvě různé metriky tedy mohou popisovat stejnou plochu. Je to dáno tím, že je na naší volbě, jaké souřadnice k popisu plochy použijeme. Už v první části tohoto textu jsme zdůrazňovali, že použité souřadnice nijak neovlivňují fyzikální podstatu toho, co popisují. Vždy lze najít nepřeberné množství různých souřadnic a tím pádem i metrik, kterými lze danou plochu vhodně popsat. Samozřejmě jsou vždy některé popisy výrazně jednodušší, lépe představitelné, snadněji se v nich počítá atd. Jak ale poznat, že různé metriky popisují stejnou plochu? Pokud tomu tak skutečně je, tak musí existovat způsob, jak z jedné sady souřadnic přejít ke druhé. I to jsme již viděli několikrát v předchozích částech. Říkáme tomu transformace souřadnic. Je to trochu zdlouhavé odvozování a není nutné se jím teď zabývat, ale zájemci si mohou níže rozkliknout ukázku, jak pomocí vhodné transformace převedeme tvar metriky \eqref{4.15} na tvar \eqref{4.14}.
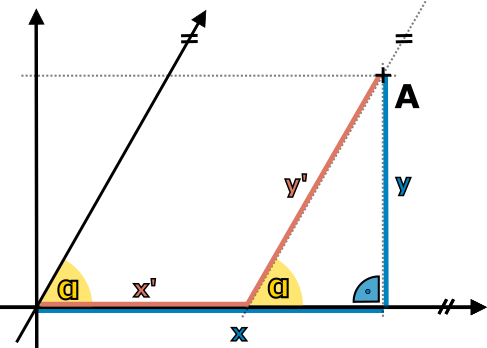
Náčrtek ukazující vztah mezi kartézskými souřadnicemi \((x,y)\) a nekolmými \((x^\prime,y^\prime)\).
Předně potřebujeme tu správnou transformaci souřadnic. Tu vyčteme z obrázku 4.34a, kde jsou naznačeny jednotlivé souřadnice pro bod A. Vztah mezi \(y^\prime\) a \(y\) najdeme pomocí pravoúhlého trojúhelníku v pravé části obrázku, plyne z něj \(y=y^\prime\sin\alpha\). I když jsme si pro jednoduchost zvolili osy souřadnic \(x\) a \(x^\prime\) totožné, samotné hodnoty souřadnic totožné nejsou, jak ukazuje obrázek. Opět s pomocí pravoúhlého trojúhelníku můžeme odvodit, že \(x=x^\prime+y^\prime\cos\alpha\).
Protože transformace je lineární (tj. souřadnice se v ní vyskytují pouze v první mocnině), budou stejné vztahy platit i pro změny souřadnic, jako jsme to už také viděli například u Lorentzovy transformace. A protože jsme v rovině, můžeme namísto konečných rozdílů \(\Delta\) opět rovnou psát nekonečně malé změny \(\text{d}x\) apod. Celkem tedy \begin{equation*} \text{d}x=\text{d}x^\prime+\text{d}y^\prime\cos\alpha, \qquad \text{d}y=\text{d}y^\prime\sin\alpha. \end{equation*} Nyní už zbývá jen tyto výrazy dosadit do \eqref{4.14}: \begin{align*} (\text{d}s)^2&=(\text{d}x)^2+(\text{d}y)^2=(\text{d}x^\prime+\text{d}y^\prime\cos\alpha )^2+(\text{d}y^\prime\sin\alpha)^2 \\ &=(\text{d}x^\prime)^2+2\text{d}x^\prime\text{d}y^\prime\cos\alpha+(\text{d}y^\prime)^2\cos^2\alpha+(\text{d}y^\prime)^2\sin^2\alpha \\ &=(\text{d}x^\prime)^2+2\text{d}x^\prime\text{d}y^\prime\cos\alpha+(\cos^2\alpha+\sin^2\alpha)(\text{d}y^\prime)^2 \\ &=(\text{d}x^\prime)^2+(\text{d}y^\prime)^2+2\text{d}x^\prime\text{d}y^\prime\cos\alpha.\\ \end{align*} V předposledním řádku jsme využili známou identitu \(\cos^2\alpha+\sin^2\alpha=1\). Vidíme tedy, že s pomocí vhodné transformace souřadnic přešla kartézská metrika na metriku zkosených souřadnic.Souřadnice se zkosenými osami jsme si ukázali ze dvou důvodů. Za prvé, jak už jsme viděli, souřadnice, které na sebe nejsou kolmé, vedou v metrice ke smíšeným členům. Za druhé, různé metriky mohou popisovat stejnou plochu, pokud mezi nimi dokážeme přejít pomocí vhodné transformace souřadnic. Popisovaná situace totiž samozřejmě nemůže být závislá na použitých souřadnicích. Například by se nám ale tento postup nepovedl, pokud bychom chtěli rovinnou metriku \eqref{4.14} převést na metriku sféry \eqref{4.13}. Můžete to zkoušet, jak chcete, ale žádnou takovou transformaci souřadnic nenajdete. Rovina a sféra se liší svojí křivostí, a proto souřadnice fungující na jedné z ploch nebudou fungovat na té druhé (na druhou stranu je dobré zdůraznit, že křivost plochy nemůže záviset na použitých souřadnicích – je invariantní podobně jako vzdálenosti). Alespoň tedy ne globálně, tj. v každém bodě. Jak už víme, pokud bychom se omezili na dostatečně malý kousek sféry, mohli bychom s k ní chovat jako k části roviny a použít tak kartézské souřadnice. Ale dřív nebo později, pro dostatečně velké vzdálenosti, by se náš popis už příliš vzdálil realitě.
Když už jsme u té roviny, ukažme si ještě, že pro určité souřadnice nemusí být v metrice dokonce ani konstantní koeficienty a přesto se jedná o rovinu. Takovým příkladem jsou polární souřadnice, kdy každý bod roviny popisujeme místo dvou kolmých vzdáleností \((x,y)\) pomocí vzdálenosti od počátku \(r\) a úhlu \(\varphi\) mezi osou \(x\) a příslušnou spojnicí bodu s počátkem (jak vidíme na obrázku 4.35 vlevo). Z obrázku je také vidět vztah mezi jednotlivými souřadnicemi (tj. daná transformace): \begin{align*}\tag{4.16}\label{4.16} x(r,\varphi)=r\cos{\varphi}, \qquad y(r,\varphi)=r\sin{\varphi}. \end{align*}
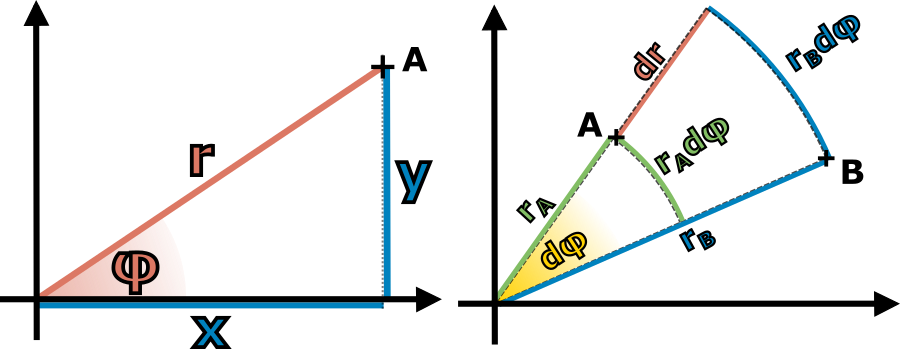
Obrázek 4.35 Vlevo: Porovnání kartézských souřadnic \((x,y)\) a polárních souřadnic \((r,\varphi)\).
Vpravo: K odvození vzdálenosti dvou blízkých bodů pomocí rozdílů polárních souřadnic.
Příslušnou metriku můžeme uhádnout opět přibližnou aplikací Pythagorovy věty na dva dostatečně blízké body. Celý postup je analogický k odvození metriky na sféře. Blízké body dělí radiální vzdálenost \(\text{d}r=r_B-r_A\) a úhel \(\text{d}\varphi=\varphi_A-\varphi_B\). Stejně jako na sféře nám nestačí úhel, ale potřebujeme délku příslušného oblouku, a ten dostaneme vynásobením úhlu \(\text{d}\varphi\) příslušným poloměrem, přičemž je jedno, kterou ze souřadnic \(r\) použijeme, protože pro dostatečně blízké body dostáváme stejný výsledek (vzpomeňte na tabulku 4.1). Celkem bude tedy metrika roviny v polárních souřadnicích \begin{equation*}\tag{4.17}\label{4.17} (\text{d}s)^2=(\text{d}r)^2+r^2(\text{d}\varphi)^2. \end{equation*} Ani zde nám nevyšel žádný smíšený člen, protože souřadnice \(r\) a \(\varphi\) jsou na sebe kolmé, respektive kolmé jsou křivky konstantních souřadnic (kružnice pro \(r=konst\) a polopřímka vycházející z počátku pro \(\varphi=konst\)). Na rozdíl od kartézské metriky \eqref{4.14} máme u jednoho z kvadrátů nekonstantní koeficient, což jsme už viděli u metriky na sféře a je to typický znak zakřivené plochy. Na druhou stranu, jak můžeme vidět v tomto případě, nemusí to být pravda vždy. Může se jednat jen o důsledek definice daných křivočarých souřadnic. Připomeňme, že pravou zkouškou, jak poznat, že daná metrika patří rovině je, dá-li se vhodnou transformací souřadnic převést na tvar \eqref{4.14}. Pomocí \eqref{4.16} skutečně jde metriku \eqref{4.17} transformovat, ale protože je k tomu potřeba znalost derivací, mohou si zájemci rozbalit toto odvození níže.
Naším cílem je ukázat ekvivalenci metrik \eqref{4.14} a \eqref{4.17}. Začneme tím jednodušším, tj. přechodem z kartézské metriky na polární. K tomu již známe správnou transformaci \eqref{4.16}. Tato transformace nám udává vztahy mezi souřadnicemi konkrétního bodu, ale my potřebujeme vztahy mezi rozdíly souřadnic. Situace zde již není tak jednoduchá jako u přechodu mezi kartézskými a kosými souřadnicemi, protože transformace \eqref{4.16} není lineární ve \(\varphi\) a proto se zde už budeme muset zabývat nekonečně malými přírůstky. Pro lepší názornost zkusíme tyto vztahy nejdříve odhadnout z obrázku níže a následně si ukážeme, jak se počítají pořádněji. Na obrázku vidíme dvě zjednodušené situace. Vlevo dva body lišící se pouze radiální souřadnicí a vpravo dva lišící se pouze úhlovou souřadnicí. Na levém obrázku vidíme hned v pravoúhlém trojúhelníku vztahy mezi přírůstky souřadnic \(\Delta x=\Delta r\cos{\varphi}\) a \(\Delta y=\Delta r\sin{\varphi}\) (které bychom dostali přímo z transformace \eqref{4.15} právě za předpokladu \(\varphi=konst\)). A tyto vztahy zůstanou v platnosti i když se budeme s body k sobě libovolně přibližovat, takže pro infinitezimálně blízké body máme jednoduše \(\text{d}x=\text{d}r\cos{\varphi}\) a \(\text{d}y=\text{d}r\sin{\varphi}\). Na pravém obrázku už je situace složitější, nějaký jasný vztah mezi přírůstky souřadnic jen tak snadno nenajdeme. Tak si ho budeme muset vytvořit. S využitím transformace \eqref{4.15} můžeme psát například \(\Delta x=r(\cos{\varphi_2}-\cos{\varphi_1})\), což nám zatím moc nepomůže. Pravou stranu ale můžeme dále rozšířit pomocí výrazu \(\Delta\varphi=\varphi_2-\varphi_1\) na následující tvar: \begin{equation*} \Delta x=r\frac{\cos{\varphi_1}-\cos{\varphi_2}}{\Delta\varphi}\Delta\varphi. \end{equation*} Pokud nyní přejdeme pomocí limity k infinitezimálnímu posunutí o \(\text{d}\varphi\) místo o konečně velké \(\Delta\varphi\), ze zlomku se stane podle definice derivace: \begin{equation*} \text{d}x=\lim_{\Delta\varphi\rightarrow 0}\Delta x=\lim_{\Delta\varphi\rightarrow 0}r\frac{\cos{\varphi_1}-\cos{\varphi_2}}{\Delta\varphi}\Delta\varphi=r\frac{\text{d}(\cos{\varphi})}{\text{d}\varphi}\text{d}\varphi=-r\sin{\varphi}\:\text{d}\varphi, \end{equation*} kde jsme využili známý fakt, že derivace funkce kosinus je mínus sinus. Přiblížením bodů k sobě se jejich původní úhlové souřadnice \(\varphi_1\) a \(\varphi_2\) přibližující k jedné společné \(\varphi\), takže mezi nimi nemusíme rozlišovat. Stejným způsobem bychom dostali \(\text{d}y=r\cos{\varphi}\:\text{d}\varphi\).
Obrázek 4.34a Vlevo: Vztah rozdílů kartézských a polárních souřadnic dvojice bodů o stejné úhlové souřadnici \(\varphi\).
Vpravo: Podobně pro dvojici bodů na stejné radiální souřadnici \(r\).
Tyto vztahy ale platí jen pro speciální případy, kdy mají oba body jednu polární souřadnici společnou. Obecně tomu tak samozřejmě být nemusí. Správný obecný výsledek dostaneme na první pohled poněkud naivním způsobem, kdy změny souřadnic prostě sečteme. Například souřadnice \(x\) se o kousek změní díky změně radiální souřadnice a o kousek také změnou úhlové souřadnice. Celkem dostáváme \(\text{d}x=\cos{\varphi}\:\text{d}r-r\sin{\varphi}\:\text{d}\varphi\) a \(\text{d}y=\sin{\varphi}\:\text{d}r+r\cos{\varphi}\:\text{d}\varphi\). Protože vám dosavadní postup může připadat neuspokojivý, ukažme si, jak se postupuje obecně. Již víme, že se ve vztazích objeví derivace. Derivace právě vystihuje, jak se hodnota nějaké funkce mění, když trochu změníme hodnotu její proměnné. Zde ale máme funkce dvou proměnných, \(x\) i \(y\) závisí na \(r\) i \(\varphi\). Musíme tedy využít pravidlo pro výpočet tzv. totálního diferenciálu (tj. malého posunutí) funkce o více proměnných, kdy derivujeme nejprve podle jedné proměnné a potom podle druhé: \begin{equation*} \text{d}x=\frac{\partial x}{\partial r} \text{d}r+\frac{\partial x}{\partial \varphi}\text{d}\varphi,\qquad \text{d}y=\frac{\partial y}{\partial r}\text{d}r+\frac{\partial y}{\partial \varphi}\text{d}\varphi. \end{equation*} Výraz typu \(\partial x/\partial r\) značí tzv. parciální derivaci, což je nástroj, který se objevuje u funkcí více proměnných a znamená pro nás, že zde derivujeme čistě podle vyznačené proměnné, a ostatní považujeme za konstanty. Spočítejme si tedy nejdříve všechny příslušné derivace: \begin{array}{ll} \frac{\partial x}{\partial r}=\frac{\partial (r\cos{\varphi})}{\partial r}=\cos{\varphi}, & \frac{\partial x}{\partial \varphi}=\frac{\partial (r\cos{\varphi})}{\partial \varphi}=-r\sin{\varphi}, \\ \frac{\partial y}{\partial r}=\frac{\partial (r \sin{\varphi})}{\partial r}=\sin{\varphi},& \frac{\partial y}{\partial \varphi}=\frac{\partial (r\sin{\varphi})}{\partial \varphi}=r\cos{\varphi}. \\ \end{array} Pro přírůstky souřadnic tedy platí stejné vztahy, jaké jsme již dříve částečně odhadli: \begin{equation*} \text{d}x=\cos{\varphi}\:\text{d}r-r\sin{\varphi}\:\text{d}\varphi, \qquad \text{d}y=\sin{\varphi}\:\text{d}r+r\cos{\varphi}\:\text{d}\varphi. \end{equation*} Po dosazení do kartézské metriky roviny dostáváme \begin{align*} (\text{d}s)^2& =(\text{d}x)^2+(\text{d}y)^2=(\cos{\varphi}\:\text{d}r-r\sin{\varphi}\:\text{d}\varphi)^2+(\sin{\varphi}\:\text{d}r+r\cos{\varphi}\:\text{d}\varphi)^2 \\ & =(\cos^2{\varphi}\:(\text{d}r)^2-2r\sin{\varphi}\cos{\varphi}\:\text{d}r\:\text{d}\varphi + r^2\sin^2{\varphi}\:(\text{d}\varphi)^2 ) + \\ &+(\sin^2{\varphi}\:(\text{d}r)^2+2r\sin{\varphi}\cos{\varphi}\:\text{d}r\:\text{d}\varphi + r^2\cos^2{\varphi}\:(\text{d}\varphi)^2 \\ & =[\cos^2{\varphi}+\sin^2{\varphi}](\text{d}r)^2+[\sin^2{\varphi}+\cos^2{\varphi}]r^2(\text{d}\varphi)^2=(\text{d}r)^2+r^2(\text{d}\varphi)^2. \end{align*}
Podobně můžeme dokázat i přechod opačným směrem. K tomu potřebujeme opačnou transformaci, tedy z kartézských do polárních souřadnic, tu můžeme vyjádřit například z \eqref{4.15} jako \begin{equation*} r(x,y)=\sqrt{x^2+y^2}, \qquad \varphi(x,y)=\arctan{\left(\frac{y}{x}\right)}. \end{equation*} Připomeňme, že \(\arctan{(...)}\) je inverzní (jinak řečeno opačná) funkce k funkci tangens. Analogicky k předchozímu platí \begin{equation*} \text{d}r=\frac{\partial r}{\partial x}\text{d}x+\frac{\partial r}{\partial y}\text{d}y, \qquad \text{d}\varphi=\frac{\partial\varphi}{\partial x}\text{d}x+\frac{\partial\varphi}{\partial y}\text{d}y. \end{equation*} Spočítejme si opět nejdříve příslušné derivace: \begin{array}{l} \frac{∂r}{∂x}=\frac{∂(\sqrt{x^2+y^2})}{∂x}=\frac{x}{\sqrt{x^2+y^2}}, \qquad \frac{∂r}{∂y}=\frac{∂(\sqrt{x^2+y^2})}{∂y}=\frac{y}{\sqrt{x^2+y^2}}, \\ \frac{∂\varphi}{∂x}=\frac{∂\left(\arctan{\left(\frac{y}{x}\right)}\right)}{∂x}=\frac{1}{1+\frac{y^2}{x^2}}\left(-\frac{y}{x^2}\right)=\frac{-y}{x^2+y^2}, \\ \frac{∂\varphi}{∂y}=\frac{∂\left(\arctan{\left(\frac{y}{x}\right)}\right)}{∂y}=\frac{1}{1+\frac{y^2}{x^2}}\left(\frac{1}{x}\right)=\frac{x}{x}\frac{1}{x+\frac{y^2}{x}}=\frac{x}{x^2+y^2}. \\ \end{array} V poslední úpravě jsme rozšířili zlomek, abychom dostali tvar podobný předchozí derivaci, protože se s ním bude lépe pracovat. Při odvozování jsme také využili tzv. řetízkové pravidlo o derivaci složené funkce a derivaci funkce \(\arctan{x}\), kterou můžeme dohledat například na internetu jako \((\arctan{x})^\prime=1/(1+x^2)\). Po dosazení do přírůstků souřadnic dostáváme \begin{equation*} \text{d}r=\frac{x\:\text{d}x}{\sqrt{x^2+y^2}}+\frac{y\:\text{d}y}{\sqrt{x^2+y^2}}=\frac{1}{r}(x\:\text{d}x+y\:\text{d}y), \qquad \text{d}\varphi=\frac{-y\:\text{d}x}{x^2+y^2}+\frac{x\:\text{d}y}{x^2+y^2}=\frac{1}{r^2}(-y\:\text{d}x+x\:\text{d}y), \end{equation*} kde jsme využili, že \(\sqrt{x^2+y^2}=r\). Toto je trochu nekonzistentní označení, protože v matematice bychom správně měli vyjadřovat přírůstky jedné sady souřadnic, v tomto případě \(r\) a \(\varphi\), pouze pomocí druhé sady souřadnic, tedy \(x\) a \(y\), ale jak uvidíme, usnadní nám to hodně opisování.
Nyní už zbývá jen dosadit do polární metriky: \begin{array}{l} (\text{d}s)^2 & =(\text{d}r)^2+r^2(\text{d}\varphi)^2=\frac{1}{r^2}(x\:\text{d}x+y\:\text{d}y)^2+r^2\frac{1}{r^4}(-y\:\text{d}x+x\:\text{d}y)^2 \\ & =\frac{1}{r^2}\left(x^2(\text{d}x)^2+2xy\:\text{d}x\:\text{d}y+x^2(\text{d}y)^2\right)+\frac{1}{r^2}\left(y^2(\text{d}x)^2-2xy\:\text{d}x\:\text{d}y+x^2(\text{d}y)^2\right) \\ & =\frac{1}{r^2}\left[(x^2+y^2)(\text{d}x)^2+(x^2+y^2)(\text{d}y)^2\right]=\frac{1}{r^2}\left[r^2(\text{d}x)^2+r^2(\text{d}y)^2\right]=(\text{d}x)^2+(\text{d}y)^2. \\ \end{array}
Pojďme si udělat takové malé obecné shrnutí. Každou plochu, ať už zakřivenou či nikoli, popisujeme pomocí dvou souřadnic. Pojďme si je označit zcela obecně \(x^1\) a \(x^2\). Toto označení nemá nic společného s mocninou, je to běžný způsob, jak se v relativitě značí souřadnice, tj. s indexem nahoře. Není to ani tak zmatečné, jak se může na první pohled zdát, protože málokdy narazíme na mocniny souřadnic, a toto označení má i své rozumné matematické důvody, které by nás ale nyní jen zbytečně zdržovaly. Již jsme například potkali \((x^1,x^2)=(x,y)\), tj. kartézské souřadnice. Pro rovinu jsme si ale představili i kosé (tj. nekolmé) souřadnice \((x^1,x^2 )=(x^\prime,y^\prime)\) a také polární \((x^1,x^2)=(r,\varphi)\). V případě sféry jsme si zase zavedli úhlové souřadnice \((x^1,x^2)=(\theta,\varphi)\).
Dále jsme viděli, že pro každou plochu, respektive pro dané zvolené souřadnice na ploše, jsme dokázali odvodit tzv. metriku, neboli předpis, jak počítat vzdálenost dvou nekonečně blízkých bodů. Ta má obecně tvar \begin{equation*}\label{4.18}\tag{4.18} (\text{d}s)^2=g_{11}(x^1,x^2)(\text{d}x^1)^2+g_{22}(x^1,x^2)(\text{d}x^2 )^2+2g_{12}(x^1,x^2)\text{d}x^1\text{d}x^2, \end{equation*} kde \(g_{11}\), \(g_{22}\) a \(g_{12}\) jsou tzv. metrické koeficienty obecně závislé na souřadnicích – jak je zdůrazněno v závorkách, ale dále to pro stručnost zápisu budeme vynechávat. Dvojka u smíšeného členu je z toho důvodu, že metrika může teoreticky vzato obsahovat dva smíšené členy \(g_{12}\text{d}x^1\text{d}x^2\) a \(g_{21}\text{d}x^2\text{d}x^1\), ale ty jsou vždy stejné, takže je píšeme dohromady (příklad vidíme v metrice \eqref{4.15}). Pokud jsou dané souřadnice na sebe kolmé, smíšený člen v metrice není. Metrické koeficienty hrají zásadní roli v matematickém popisu zakřivení a následně i obecné relativity. Více se o jejich významu můžete dozvědět níže.
Neprve malé připomenutí. Matematicky vzato nám metrické koeficienty umožňují spočítat reálnou vzdálenost mezi dvěma body na ploše či v prostoru pomocí použitých souřadnic. Při používání kartézských souřadnic v rovině či prostoru jsme zvyklí na to, že rozdíly souřadnic jsou přímo vzdálenosti, které dané body dělí ve dvou (či třech) na sebe kolmých směrech a přímou vzdálenost pak jen vypočítáme pomocí Pythagorovy věty. Důsledkem tohoto přímého vztahu vzdáleností a kartézských souřadnic je, že metrické koeficienty u kvadrátů souřadnic v kartézské metrice jsou jedničky a smíšené členy jsou nulové \eqref{4.14}. Viděli jsme ale například kosé souřadnice \((x^\prime,y^\prime)\), kde se nám už situace komplikuje o křížový člen (metrika \eqref{4.15}) anebo polární souřadnice \eqref{4.17}, kde se objeví metrický koeficient \(r^2\) díky úhlové povaze souřadnice \(\varphi\).
U přímočarých souřadnic (tedy takových, kde křivky konstantní souřadnice jsou přímky – to byly právě např. kartézské a kosé) jsou metrické koeficienty neměnící se konstanty, takže metrické vztahy platí na jakoukoli vzdálenost. Proto můžeme metriku v těchto případech používat pro konečné vzdálenosti \(\Delta s\) stejně jako infinitezimální \(\text{d}s\) a její tvar zůstává stejný, protože u přímočarých souřadnic je použitá geometrie nezávislá na měřítku (jak ilustruje obrázek níže). Použijeme-li ale v rovině křivočaré souřadnice (například polární \((r,\varphi)\), takže stačí, aby byla křivočará jen jedna) je již velmi obtížné ba třeba i nemožné najít obecný vztah mezi vzdáleností dvou bodů a rozdíly jejich souřadnic. Řešením je pracovat s nekonečně malými změnami souřadnic a vzdáleností, protože pak prakticky vzato pracujeme opět s (přibližnými) úsečkami – například vzdálenost \(r\text{d}\varphi\) v dolní části obrázku je striktně vzato část kružnice, ale v infinitezimálním (tedy dostatečně malém) přiblížení je nerozeznatelná od úsečky. Jak už jsme zmiňovali, cenou za toto zjednodušení je, že jsme tak hledanou vzdálenost rozdělili na teoreticky nekonečně mnoho nekonečně malých úseků, takže prosté sčítání nám zde nepomůže. Je třeba integrovat. Zatím jsme viděli jen velmi elementární případy, protože obecně se může jednat o dost komplikovaný výpočet, ale v principu to jde. V rovině či v prostoru se mohou křivočaré souřadnice zdát jako zbytečná komplikace (i když existují aplikace, kdy jsou křivočaré souřadnice vhodnější), ale na zakřivených plochách jsou nutností, protože zde samozřejmě nejsou přímočaré souřadnice globálně možné.
Nahoře: Geometrie svazující přímočaré souřadnice a vzdálenost bodů v rovině platí pro libovolně velké vzdálenosti.
Dole: U křivočarých souřadnic, ať už v rovině nebo nebo zakřivené ploše, již používáme nekonečně malá posunutí. Máme tak relativně jednoduché vztahy mezi vzdáleností dvou nekonečně blízkých bodů a jejich rozdíly souřadnic. Cenou, kterou za to platíme je, že výslednou vzdálenost musíme spočítat jako součet nekonečně mnoha nekonečně malých kousků, tzv. integrací.
V kapitole o neeukleidovské geometrii jsme například viděli hyperbolický paraboloid jako ukázku plochy se zápornou křivostí. Představme si nyní, že tato plocha vznikne z roviny jejím zakřivením jako na obrázku níže. Rovina byla původně popsána kartézskými souřadnicemi \((x,y)\) a jak jsme se už zmiňovali, podobné souřadnice můžeme použít i pro popis sedlové plochy, kterou můžeme vytvořit tak, že každému bodu v rovině \(xy\) přiřadíme výšku například podle předpisu \(z=x^2-y^2\). Dá se ukázat (i když my tento výpočet zde provádět nebudeme), že metrika pro plochu pak bude mít tvar \begin{equation*} (\text{d}s)^2=(4x^2+1)(\text{d}x)^2+(4y^2+1) (\text{d}y)^2-4xy\:\text{d}x\:\text{d}y. \end{equation*} Za prvé vidíme, že souřadnice na ploše již nejsou kolmé, protože se nám objevil křížový člen. Tuto skutečnost nám ilustruje obrázek níže, kde máme srovnání obou ploch. Souřadnicové čáry na sedlové ploše na sebe opravdu již nejsou všude kolmé díky deformaci plochy. Ta se projevila právě v odlišnosti metrických koeficientů. Například si ale můžeme všimnout, že uprostřed pohledu, tj. kolem počátku souřadnic, jsou na sebe čáry ještě přibližně kolmé, což je dáno tím, že křížový metrický koeficient \(4xy\) je zde blízký nule. Je to podobná situace, jako když používáte mapu ve zvlněném terénu. Pochodujeme-li například po horách, můžeme sice svůj pohyb sledovat na mapě, což je projekce okolního terénu do roviny, ale vzdálenost, kterou ujdeme, se nebude shodovat se vzdáleností, o kterou se přitom posuneme na mapě a naopak. Důvodem je právě zakřivení terénu. K určení reálné vzdálenosti z mapy je třeba znát navíc informaci o lokální geometrii – a tu v sobě právě obsahuje metrika.
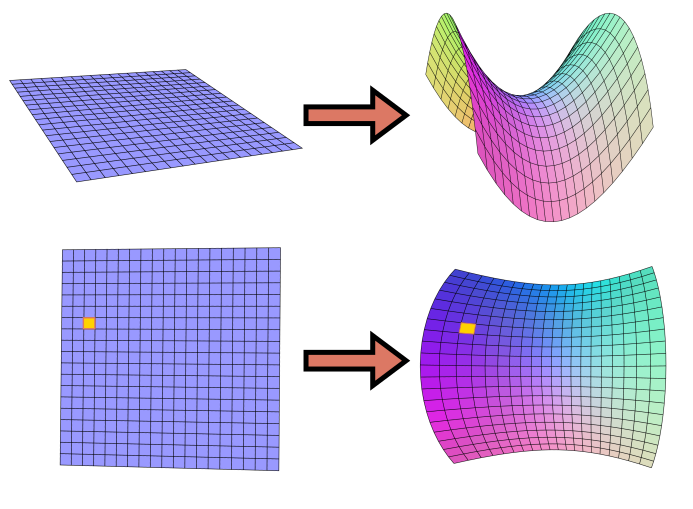
Nahoře:Sedlová plocha vytvořená deformací roviny. Barvy jsou čistě pro přehlednost, nemají žádný hlubší význam. Souřadnicové čáry na sedlové ploše jsou zdeformované oproti rovině. Již nejsou všude navzájem kolmé, jak ukazuje i metrika. Deformaci vidíme i na žlutě zvýrazněném políčku.
Dále si představme, že bychom chtěli změřit vzdálenost pouze třeba ve směru x. Všechny členy v metrice obsahující \(\text{d}y\) pak budou nulové a nám zbyde \begin{equation*} (\text{d}s)^2=(4x^2+1)(\text{d}x)^2\implies\text{d}s=\sqrt{4x^2+1}\text{d}x. \end{equation*} Výsledný vztah znamená, že když se posuneme čistě ve směru souřadnice \(x\) o malý kousek \(\text{d}x\), reálně uražená vzdálenost na ploše \(\text{d}s\) bude ve skutečnosti většinou větší, protože pod odmocninou bude vždy výraz větší nebo rovný než jedna. Pokud bychom byli přesně nad kartézskou osou \(y\) (tj. tam, kde \(x=0\)), pak jedině platí rovnost mezi \(\text{d}s\) a \(\text{d}x\) a čím dál od osy tento posun provedeme, tím je \(ds\) větší, a to symetricky na obě strany díky \(x^2\) v metrickém koeficientu. Pokud si tedy danou plochu představíme jako zdeformovanou rovinu, metrický koeficient nám zde prakticky dává informaci o natažení (případně smrštění) plochy v daném místě a směru. Tato souvislost pro nás bude velmi důležitá i později, až se budeme zabývat reálným měřením času a vzdáleností v přítomnosti gravitace.
Zároveň si můžeme připomenout základní komplikaci a zároveň filozofii diferenciální geometrie. Obecně je obtížné najít vztah mezi posunutím i třeba jen v jedné souřadnici, např. o \(\Delta x\), tedy o konečnou hodnotu souřadnice \(x\), a reálně uraženou vzdáleností na ploše \(\Delta s\). Proto hledáme zjednodušené vztahy mezi infinitezimálními posunutími pomocí matematických metod, jako jsou derivace. Ty jsou ale platné právě jen pro nekonečně malá posunutí a pro konečná je použít nemůžeme. Stačí se podívat na výraz spojující \(\text{d}s\) a \(\text{d}x\) – jakou hodnotu máme dosadit za \(x\), když se přesouváme ze souřadnice \(x_1\) na \(x_2\)? Při konečných posunutích neexistuje správná odpověď, maximálně může dosadit třeba hodnotu někde uprostřed mezi začátkem a koncem a dostat jen přibližný výsledek. Přesnou odpověď dostaneme jen integrací. Symbolicky se zapisuje $$ \Delta s=\int\text{d}s=\int\sqrt{4x^2+1}\text{d}x. $$ Nejsme tu od toho, abychom se učili integrovat. Navíc zrovna tento integrál nepatří mezi nejlehčí (je to mimochodem stejný integrál, jako kdybychom hledali délku paraboly, což je vlastně přesně to, co děláme – křivky konstantní souřadnice na sedlové ose jsou paraboly). Naštěstí se můžeme dočkat odpovědi i bez znalosti pokročilé matematiky. Výpočet můžeme zadat na stránce Wolfram Alpha (do zadávací lišty stačí zadat „integral sqrt(4x^2+1)“) a najdeme výsledný předpis. Není to zrovna hezký vzorec a k ničemu ho nevyužijeme, takže nemá moc smysl ho zde přepisovat. Je pro nás ale důležité, že to v principu jde. Kdybychom pak postupovali čistě ve směru změny souřadnice \(y\), bude celý postup identický.
Obecnému případu, kdy chceme spočítat vzdálenost uraženou mezi body lišícími se v obou souřadnicích, se zde již věnovat nebudeme. Za prvé je matematicky výrazně komplikovanější, protože vede na tzv. křivkový integrál, který už je opravdu zcela mimo záběr tohoto textu. Za druhé je i koncepčně složitější na řešení, protože nestačí jen zadat souřadnice počátečního a koncového bodu. Výsledek také závisí na dráze, kterou od jednoho bodu k druhému zvolíme. A i v případě, že nás zajímá opravdu nejkratší vzdálenost obou bodů, to znamená délka části geodetiky, která je spojuje, se nejedná o jednoduchý problém, protože geodetiky mohou být v závislosti na dané ploše obecně velmi komplikované křivky, pro které často neexistuje přímý matematický předpis a je třeba je hledat numericky pomocí počítače. Z toho důvodu se v našich relativistických výpočtech budeme věnovat zejména situacím, kde se bude měnit třeba jen jedna souřadnice, nebo kde můžeme složité integrování nějak chytře obejít.
Jako cvičení si můžete zkusit identifikovat metrické koeficienty pro všechny metriky, které jsme už potkali, a doplnit je do tabulky níže. Správné řešení si můžete pak rozkliknout pod tabulkou.
| Tabulka 4.3 Metrické koeficienty pro již zmíněné plochy a souřadnice | ||||
|---|---|---|---|---|
| Plocha | Souřadnice | \(g_{11}\) | \(g_{22}\) | \(g_{12}=g_{21}\) |
| Rovina | Kartézské \((x,y)\) | |||
| Kosé \((x^\prime,y^\prime)\) | ||||
| Polární \((r,\varphi)\) | ||||
| Sféra o poloměru \(R\) | Úhlové \((\theta,\varphi)\) | |||
| Tabulka 4.3a Metrické koeficienty pro již zmíněné plochy a souřadnice | ||||
|---|---|---|---|---|
| Plocha | Souřadnice | \(g_{11}\) | \(g_{22}\) | \(g_{12}=g_{21}\) |
| Rovina | Kartézské \((x,y)\) | \(1\) | \(1\) | \(0\) |
| Kosé \((x^\prime,y^\prime)\) | \(1\) | \(1\) | \(\cos{\alpha}\) | |
| Polární \((r,\varphi)\) | \(1\) | \(r^2\) | \(0\) | |
| Sféra o poloměru \(R\) | Úhlové \((\theta,\varphi)\) | \(R^2\) | \(R^2\sin^2{\theta}\) | \(0\) |
Nic nám nebrání tento matematický popis rozšířit o dimenzi výše (nebo prakticky na libovolný počet dimenzí, ale nepředbíhejme). Prostor popisujeme obecně pomocí tří nějakých souřadnic, tedy \((x^1,x^2,x^3)\), přičemž naše staré známé kartézské souřadnice \((x,y,z)\) nejsou jediná možnost. Dalším příkladem jsou třeba sférické souřadnice \((r,\theta,\varphi)\), což jsou už nám známé úhly na sféře s přidanou vzdáleností od počátku \(r\), čímž dokážeme popsat prakticky celý prostor. I prostor má svojí metriku, v případě kartézských souřadnic je to jednoduše \((\text{d}s)^2=(\text{d}x)^2+(\text{d}y)^2+(\text{d}z)^2\) (což jsme viděli už v rovnici \eqref{4.11} pro konečné rozdíly souřadnic). Metrické koeficienty jsou v tomto případě opět samé jedničky, ale obecně to tak být nemusí. Čistě jen pro zajímavost si můžeme prozradit tvar metriky ve sférických souřadnicích: \((\text{d}s)^2=(\text{d}r)^2+r^2(\text{d}\theta)^2+r^2\sin^2{\theta} (\text{d}φ)^2\). Podobně jako u radiálních souřadnic se dá ukázat, že mezi prostorovou metrikou v kartézských a ve sférických souřadnicích se dá přecházet, protože obě popisují stejný euklidovský prostor (podobně jako polární souřadnice stále popisují rovinu). Mimochodem, všimněme si, že pro \(r=konst=R\), tj. omezíme-li se na oblast o konstantní vzdálenosti \(R\) od počátku souřadnic (tedy sféru o poloměru \(R\)), bude změna v radiální souřadnici \(\text{d}r\) nulová a dostáváme tak metriku sféry \eqref{4.13}.
Zobecnění vztahu \eqref{4.18} pro prostor je pak celkem přímočaré, prostě místo do dvou budeme počítat do tří. Obecně má tak prostorová metrika tvar \begin{equation*}\label{4.19}\tag{4.19} (\text{d}s)^2=g_{11}(\text{d}x^1)^2+g_{22}(\text{d}x^2)^2+g_{33} (\text{d}x^3)^2 +2g_{12}\text{d}x^1\text{d}x^2+2g_{13}\text{d}x^1 \text{d}x^3+2g_{23}\text{d}x^2\text{d}x^3, \end{equation*} kde jsme pro stručnost už znovu nezdůrazňovali, že každý metrický koeficient \(g_{ij}\) může obecně záviset na všech souřadnicích, takže \(g_{11}(x^1,x^2,x^3)\) atd. Výraz typu \((\text{d}x^1)^2\) je třeba chápat jako změna v souřadnici \(x^1\), to celé na druhou. Vidíme tedy praktický příklad toho, jak prostým rozšířením matematického popisu ploch, jejichž zakřivení si představit dokážeme, můžeme popsat i prostor – v principu třeba i zakřivený, což už si představit příliš nedokážeme. A tím samozřejmě nekončíme. Naším konečným cílem je matematický popis zakřiveného prostoročasu. Protože ten je obecně popsán čtyřmi souřadnicemi, budou i indexy v metrice nabývat čtyř hodnot. Něco takového jsme už ale vlastně viděli ve třetí části o STR. V ní jsme popsali prostoročas pomocí souřadnic \((x^0,x^1,x^2,x^3)=(ct,x,y,z)\) – relativistickou konvencí je totiž přiřazovat časové souřadnici číslo indexu nula – a následně jsme odvodili tzv. prostoročasový interval (3.15): \begin{equation*} (\Delta s)^2=-c^2 (\Delta t)^2+(\Delta x)^2+(\Delta y)^2+(\Delta z)^2, \end{equation*} což je prostoročasová „vzdálenost“ mezi nějakými dvěma událostmi, na které se všichni inerciální pozorovatelé shodnou podobně jako se v klasické fyzice všichni pozorovatelé shodnou na vzdálenosti dvou bodů. První člen by se správně vzato měl podle naší konvence psát jako \(-[\Delta(ct)]^2\), tedy „mínus změna v souřadnici c krát t“, ale protože \(c\) je konstanta, můžeme ji z té změny vytknout a výraz tak mírně zpřehlednit.
Rovnice (3.15) je prakticky vzato metrikou námi zavedeného prostoročasu s jednou malou výjimkou – předepisuje jak spočítat „vzdálenost“ pro libovolně vzdálené události, ne jen ty nekonečně blízké. To ale snadno vysvětlíme pohledem na příslušné metrické koeficienty. U prostorových souřadnic jsou to jedničky stejně jako u kartézského prostoru: \(g_{11}=g_{22}=g_{33}=1\). V případě časové souřadnice \(x^0=ct\), je příslušný metrický koeficient \(g_{00}=-1\) (to proto, že konstantu \(c\) jsme učinili přímo součástí té souřadnice, takže v koeficientu před přírůstkem souřadnice nevystupuje – což může být na první pohled matoucí, proto to zdůrazňujeme). Jelikož jsou všechny metrické koeficienty konstanty, je tento prostoročas z geometrického hlediska plochý, tedy nezakřivený. Stejně jako u roviny tedy můžeme výraz (3.15) přepsat rovnou v infinitezimálním tvaru (tj. vyměnit \(\Delta\) za \(\text{d}\)): \begin{equation*}\tag{4.20}\label{4.20} (\text{d}s)^2=-c^2 (\text{d}t)^2+(\text{d}x)^2+(\text{d}y)^2+(\text{d}z)^2. \end{equation*} Jak už jsme se zmiňovali, podobně jako plochý prostor nazýváme eukleidovský (a nebylo to jen na počest Eukleida, ale také jako odlišení od zakřivených prostorů), má i plochý prostoročas své jméno: Minkowského prostoročas. Nejedná se tedy o jakýkoli prostoročas, ale pouze ten plochý. To je hřiště speciální teorie relativity. Obecná relativita přidává zásadní a nezbytnou komplikaci. V přítomnosti gravitace je prostoročas zakřiven, tj. přestává být v dané oblasti plochý, a jeho metrika má (v závislosti na použitých souřadnicích) obecně nekonstantní koeficienty. Pokud si uvědomíme, že máme čtyři souřadnice a každý metrický koeficient má dva indexy, dohromady dostáváme \(4\cdot4=16\) možností. To je \(16\) matematických funkcí, které bychom potřebovali v principu znát, abychom dokázali například předem spočítat trajektorii tělesa obíhající nějakou hvězdu. Ve skutečnosti sice nepotřebujeme znát všech \(16\) díky tomu, že křížové koeficienty jsou symetrické – například \(g_{01}=g_{10}\), \(g_{12}=g_{21}\) atd., a sami si můžete rozmyslet, že nám díky této vlastnosti stačí znát jen \(10\) koeficientů, ale to je stejně pořád docela hodně. Ani zde nebudeme vypisovat obecný tvar prostoročasové metriky podobně jako u rovnice \eqref{4.19}, protože už je to opravdu dlouhý a špatně přehledný matematický výraz.
Opět ale nevěšme hlavu pod náporem komplikované matematiky. Nyní jsme si již řekli vše podstatné, abychom se mohli znovu naplno ponořit do fyziky. V následující kapitole si ukážeme nejjednodušší příklad relativistického popisu gravitačního pole, tzv. Schwarzschildův prostoročas. Jeho matematický popis snad ještě zvládneme a budeme si tak na něm moci celou řadu věcí ukázat a ba i spočítat.
Shrnutí kapitoly 4.2
Na zakřivených plochách neplatí eukleidovská geometrie, kterou známe z roviny. V daném místě plochy rozlišujeme kladnou, nulovou a zápornou křivost.
Rozlišujeme také vnitřní a vnější geometrii. Vnější odpovídá tomu, jak je plocha zakřivená v prostoru, jedná se tedy o pohled „shora“ – mimo danou plochu. Vnitřní geometrie vyjadřuje geometrické vlastnosti uvnitř plochy samotné.
Existují plochy různě orientované v prostoru (tj. vnější geometrií) ale se stejnou vnitřní geometrií. Příkladem je rovina a válcová plocha.
Pro každou plochu dokážeme určit tzv. metriku, tj. vzorec pro výpočet kvadrátu vzdálenosti dvou nekonečně blízkých bodů. Jedná se o matematické přiblížení, kdy relativně jednoduše pracujeme s nekonečně malými veličinami (typicky přírůstky souřadnic jako \(\text{d}x\) nebo \(\text{d}\varphi\), a abychom pak spočítali konečnou vzdálenost dvou bodů, musíme „posčítat nekonečně mnoho nekonečně malých kousků“, což je matematický proces zvaný integrace. Tvar metriky závisí také na použitých souřadnicích. Dvě různé metriky mohou popisovat stejnou plochu, pokud mezi nimi můžeme přejít transformací souřadnic.
Ač se nám těžko představuje, teoreticky je možné, aby byl zakřivený i prostor. Znamená to, že by v něm obecně neplatila eukleidovská geometrie, ale přesto by se na dostatečně malých škálách mohl jevit plochý, podobně jako povrch koule na malých škálách vypadá jako rovina. Kosmologická otázka ohledně geometrie našeho vesmíru stále není uzavřena, a v budoucnu bude její zodpovězení nutně zahrnovat velmi přesná geometrická měření na obrovské vzdálenosti.
Obecná relativita popisuje gravitaci jako zakřivení prostoročasu (zakřivení prostoru pro úplný popis nestačí). To znamená, že na prostoročas zavedený speciální relativitou aplikuje matematiku popisující zakřivené plochy zobecněnou na čtyři souřadnice, jednu časovou a tři prostorové. Konkrétně řečeno, v prostoročasovém intervalu, což je prakticky metrika prostoročasu, budou v závislosti na použitých souřadnicích nekonstantní koeficienty.