Relativistická dílna
Obecné informace a shrnutí průběhu dílny
Tato stránka popisuje návrh výukové sekvence pro učitele fyziky, kterou je možné použít pro seznámení středoškolských studentů se základy obecné teorie relativity (OTR). Používám pro ni název dílna (jako ekvivalent anglického slova workshop), protože si zde klademe za cíl používat praktické aktivity (zejména spojené s neeukleidovskou geometrií), a být tím pádem co nejnázornější. Dílna byla již několikrát zrealizována pro studenty, vždy jako jednorázový seminář, ale je možné ji rozdělit do několika vyučovacích hodin. Doporučená délka jsou tři až čtyři vyučovací hodiny. Program dílny klade důraz na flexibilitu. Ne všechny prezentované aktivity je nutné zařadit a téměř všechny lze provést ve zkrácené podobě. Tato dílna byla už obšírněji popsána v sérii článků v Československém časopisu pro fyziku (čísla 2-5, ročník 2020), tato stránka má sloužit především jako praktický průvodce pro učitele. Budeme se zde tedy snažit o stručnost, věcnost a zaměříme se na praktickou stránku věci. Většina myšlenek v této dílně je obsažena i v učebním textu na tomto webu, zejména v kapitole 4.2, její pročtení tedy doporučujeme.
V ideálním případě následuje OTR až po tématu speciální teorie relativity (STR). Na druhou stranu, workshop je koncipován tak, aby žádné předchozí znalosti z STR nebyly potřeba (jak uvidíme, jednou v části o systémech globální navigace na nás na chvilku STR bude muset vykouknout, ale tím se nenecháme rozhodit). Naší primární snahou je ukázat studentům, co je myšleno frází "Gravitace je zakřivení prostoročasu", což je stručné vyjádření pravděpodobně nejdůležitější myšlenky OTR. Z toho plyne, že se zde budeme věnovat těm dvěma důležitým slovům, prostoročasu a zakřivení. Prostoročas je právě typicky zaveden již v STR, ale my se ho pokusíme, aby nutnost jeho zavedení vyplynula jako hlavní závěr našeho povídání. To znamená, že ačkoli je předchozí znalost alespoň základů STR výhodou, nepovažujeme ji za nutnou, aby si student z této dílny něco odnesl. Tím má učitel větší volnost v tom, kdy a pro koho tuto dílnu zařadit. Zda v běžné výuce fyziky, na semináři či obecně jako jednorázovou odpolední akci pro zájemce (tuto verzi jsem zatím vždy volil já). Kromě praktických úloh je připraveno i několik appletů, které geometrické aktivity ilustrují. Souhrnně je můžete najít na zvláštní stránce a v textu na ně budeme jednotlivě na relevantních místech odkazovat. Při dílnách se mi velmi osvědčily. Zejména na základě zpětné vazby studentů se ukázalo, že každý reaguje lépe na jiný druh reprezentace (někdo má radši animace, někdo praktické aktivity, někdo radši pracuje s papírem, jiný upřednostňuje 3D-modely), takže osobně doporučuji tyto různé verze kombinovat. Applety je možné využít jako demonstrační ukázku, anebo v případě více času je můžeme nechat prozkoumat studenty.
Na obrázku máme naznačenou strukturu celé dílny. Zakřivení prostoročasu je příliš komplikované, abychom s ním hned začali pracovat, tak si zkusíme situaci nejdříve zjednodušit. Prakticky vzato za účelem výkladu zkusíme tento komplikovaný pojem rozdělit na dva menší, na zakřivení prostoru a "zakřivení" času (čímž máme na mysli gravitační dilataci času), a podívat se na ně separátně. I to je ale problém, protože zakřivený trojrozměrný prostor si jen tak někdo nepředstaví a ani nejde pořádně vizualizovat. Půjdeme tedy ještě o dimenzi níže k zakřiveným plochám. S těmi už pracovat dokážeme. První a největší část dílny je tedy věnována neeukleidovské geometrii na plochách. Tu se pak pokusíme zobecnit na prostor. Následně se pokusíme ukázat jistou podobnost mezi chováním trajektorií pohybujících se bodů na zakřivených plochách (potažmo v zakřiveném prostoru) a těles v přítomnosti gravitace. Ukážeme, že gravitaci ale nestačí popisovat jako pohyb v zakřiveném prostoru, protože tak nedokážeme zreprodukovat celou řadu reálných jevů, například uzavřené orbity a zejména volný pád. Chybí nám zde druhá, stejně nezbytná část, dilatace času.
Realitu gravitační dilatace času budeme demonstrovat popisem reálného experimentu a následně zjednodušeným popisem, jak se musí s dilatací času technicky pracovat v satelitních systémech globální navigace. Pro názornost si spočítáme i konkrétní příklad. V závěru dílny se podíváme na volný pád s pomocí primitivního prostoročasového diagramu a ukážeme, jak jeho překreslení na zakřivenou plochu ilustruje, že kámen začne padat díky zakřivení prostoročasu.
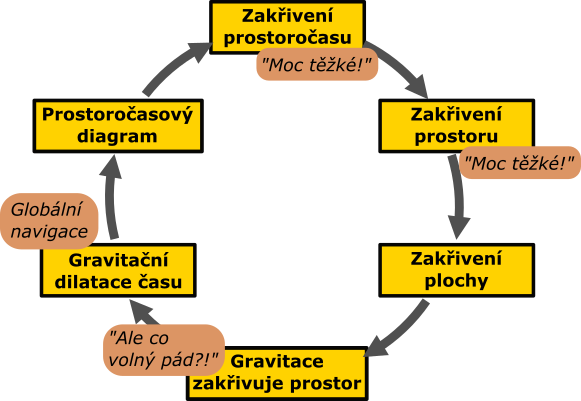
Obrázek 1 Schéma struktury dílny. Začínáme nahoře a postupujeme podle šipek.
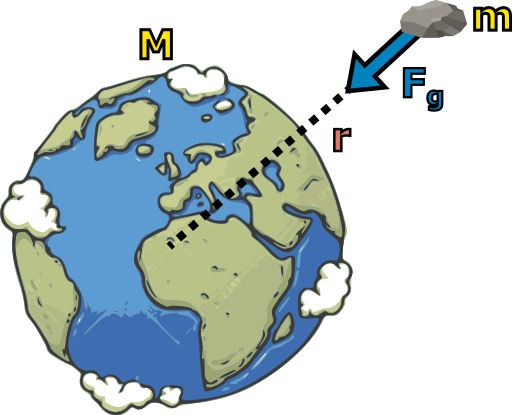
Před začátkem praktické části dílny zařazuji krátký úvod, ve kterém zaprvé nastíníme cíl celé dílny, tj. pochopení zmíněné věty "Gravitace je zakřivení prostoročasu.", a za druhé okomentujeme, proč vlastně budeme řešit "nový" způsob popisu gravitace, když existuje Newtonův gravitační zákon, který si říkáme i na střední škole. Podle něj spočítáme velikost gravitační síly \(F_g\) mezi dvěma hmotnými body o hmotnostech \(m\) a \(M\) o vzájemné vzdálenosti \(r\) jako \begin{equation}\label{Newton} F_g=\frac{GmM}{r^2}, \end{equation} kde \(G\) je Newtonova gravitační konstanta (někdy také označovaná \(\kappa\)). Důvodem, proč bylo třeba hledat novou, relativistickou teorii gravitace, je neslučitelnost tohoto vztahu se speciální teorií relativity. Vztah \eqref{Newton} totiž v sobě obsahuje tzv. okamžité působení na dálku, kdy je velikost gravitační síly dána vzdáleností těles a nijak nezávisí na čase. Pokud bychom tedy teoreticky pohnuly jedním z těles, druhé se o tom "dozví" okamžitě, ať už se nachází libovolně daleko. To je ale v rozporu s STR, protože podle ní se žádná informace nemůže šířit rychleji než světlo ve vakuu. OTR vznikla (nejenom) díky snaze tento rozpor vyřešit.
Během dílny používám prezentaci pro ilustrace a propojení jednotlivých aktivit. Dávám ji také k dispozici, ačkoli není nijak graficky atraktivní, jako pomocný základ, který si může každý snadno upravit podle svého uvážení. Pokud vás dílna zaujme a budete ji chtít se svými studenty zrealizovat, či máte-li k ní nějaký dotaz či připomínku, pište prosím na matej.rys gmail.com.
gmail.com.
Neeukleidovská geometrie (1-2 vyučovací hodiny)
Pomůcky: Do dvojice či malé skupiny potřebujeme - nůžky, lepidlo či průhlednou lepenku, lihové fixy, nafukovací balónek, několik úzkých proužků papíru (lze využít tuto kopii k rozstříhání podél přerušovaných čar). Pro učitele doporučujeme velký nafukovací míč jako demonstrační pomůcku. Ideální je míč s potiskem glóbu (případně je možné použít skutečný glóbus) kvůli vyznačeným zeměpisným poledníkům a rovnoběžkám, případně plážový míč se švy jako poledníky (vizte obrázek 2).
Na začátek naší exkurze do neeukleidovské geometrie si se studenty připomeneme několik základních tvrzení eukleidovské geometrie, které se běžně ve škole učíme, abychom začali něčím známým: \begin{array} {l l} \label{2}\tag{2} \bullet & \text{Nejkratší spojnice dvou bodů je úsečka (tj. část přímky).} \\ \bullet & \text{Součet všech vnitřních úhlů v trojúhelníku je }180^°\text{.} \\ \bullet & \text{Rovnoběžky se nikdy neprotnou (respektive kolmá vzdálenost rovnoběžek je všude stejná).} \\ \bullet & \text{Mezi poloměrem kružnice }r\text{ a jejím obvodem }o\text{ platí vztah }o=2\pi{}r\text{.} \\ \end{array}
Všechna tato tvrzení platí v rovině i v eukleidovském prostoru. My si nyní vyzkoušíme jejich platnost na různých zakřivených plochách. Nejjednodušším, dobře představitelným a zároveň snadno realizovatelným příkladem je sféra. Mohli bychom samozřejmě studentům rozdat například volejbalové míče půjčené z kabinetu tělocviku, ale snadnější pro nás budou nafukovací balónky. To nejsou sice přesné sféry, ale jsou jí dostatečně podobné (a hlavně se jedná, jak uvidíme, o stejný typ geometrie).
Geometrie na sféře
Na začátek požádáme studenty, aby na balónku vyznačili dva body a zkusili vyznačit jejich nejkratší spojnici. Sami jistě přijdou na to, že k tomu můžeme použít například provázek, ohebné pravítko, anebo právě úzký proužek papíru. I tyto pomůcky můžete studentům poskytnout, osobně preferuji proužky papíru, protože se dají na balónek rovnou místo kreslení fixou přilepit. Je zcela zjevné, že spojnice bodů na sféře nemůže být úsečka (v případě sféry se jedná vždy o část tzv. hlavní kružnice, tedy kružnice se středem ve středu koule a stejným poloměrem - jak můžeme demonstrovat v tomto appletu). Přidáním třetího bodu a dalších dvou nejpřímějších spojnic můžeme vytvořit trojúhelník. Nyní můžeme využít buď malého (či ohebného) úhloměru, abychom změřili vnitřní úhly. Zjistíme, že jejich součet je vždy větší než \(180^°\). Pokud se nechceme zdržovat s úhloměry, můžeme se případně studentů zeptat, zda je napadne, jak zkonstruovat trojúhelník, u kterého bude součet vnitřních úhlů zjevný. Můžeme jim pomoci pohledem na glóbus. Úhel mezi rovníkem a poledníky je \(90^°\), takže stačí vybrat trojúhelník, který tvoří průsečíky dvou na sebe kolmých poledníků a rovníku.
U třetího geometrického tvrzení s rovnoběžkami je třeba malá diskuze. Co to znamená rovnoběžky na sféře? Určitě zde nevytvoříme přímku, takže rozhodně nepůjde o klasické pojetí rovnoběžek. Může nás napadnout využít zeměpisné rovnoběžky, tedy kružnice konstantní zeměpisné šířky. Ty nám na první pohled při pohledu mimo sféru jistě připadají navzájem rovnoběžné. Ty nám ale nebudou vyhovovat z jiného důvodu. Nejedná se totiž o nejkratší možné spojnice dvou bodů na sféře. V předchozích případech jsme používali například proužky papíru, abychom našli nejkratší spojnici. Důvodem je, že podobně jako u úsečky v rovině, nejkratší spojnice je ta, která na cestě k cíli zbytečně nezatáčí ani na jednu stranu, jde stále "rovně" - ale toto rovně je z pohledu někoho na té ploše, ne z pohledu zvnějšku. Narážíme tu na problematiku vnitřní vs. vnější geometrie, ke které se vrátíme později. Proužek papíru nám pomohl tuto nejkratší a zároveň nejpřímější spojnici najít, protože sám o sobě je rovný když ho například položíme na stůl, ale díky své flexibilitě se dokáže přizpůsobit zakřivení dané plochy, aniž by "zatočil doprava či doleva". Toto zobecnění úsečky jako nejpřímější spojnice pro zakřivené plochy se nazývá geodetika, a v naší dílně bude, stejně jako v celé OTR, hrát hlavní roli. Vyzbrojeni tímto novým pojmem můžeme krásně ukázat, že zeměpisná rovnoběžka není geodetikou na sféře (protože ty, s výjimkou rovníku, nejsou hlavními kružnicemi). Stačí zkusit přiložit proužek papíru na rovnoběžku. Pokud nebude příliš krátká, nepodaří se vám to tak, aby papír plně ležel na ploše. Podobně si můžeme představit, že chceme vyrazit ve směru rovnoběžky a budeme chtít jít stále rovně. Přiložením geodetického papírku zjistíme, že jít rovně znamená uhnout z rovnoběžky. Opačně řečeno, chcete-li jít stále po zeměpisné rovnoběžce, musíte neustále zatáčet. Opět můžeme tuto aktivitu doplnit využitím appletu, případně webové stránky Flightconnections.com, která nám na mapě ukáže trajektorie letů mezi velkými světovými městy. Zejména u mezikontinentálních letů mezi městy na podobné zeměpisné šířce je vidět, jak letadlo zdánlivě zahýbá hodně na sever nebo na jih. Nejkratší a tím pádem nejúspornější cesta (nepočítáme-li vzdušné proudy) vede totiž po geodetice. Celkem tedy vidíme, že zeměpisná rovnoběžka, ačkoli z vnějšku vypadá rovná, je z hlediska dané plochy (tj. vnitřní geometrie) ekvivalentem zahýbající křivky v rovině. A v relativitě upřednostňujeme pohled vnitřní geometrie, protože naším finálním cílem je zkoumat geometrii prostoročasu, a na ten se nemůžeme podívat z nějakého hypotetického vyššího rozměru. Pohled vnější geometrie, tj. jak je daná plocha zakřivená v prostoru, pro nás tedy není ten směrodatný. Z toho důvodu za rovnoběžky v geometrickém slova smyslu budeme považovat dvě geodetiky, které jdou alespoň zpočátku stejným směrem. Poměrně názorným příkladem jsou dva blízké poledníky vycházející z rovníku. Jsou zpočátku rovnoběžné (kolmé na rovník), ale na glóbu vidíme (nebo si sami vyzkoušíme), že se k sobě přibližují a dříve či později se protnou.
Poslední tvrzení s kružnicí můžeme také prakticky ověřit. Stačí si zvolit na sféře bod jako střed a s pomocí geodetiky vyznačit dostatečně velké množství bodů o stejné vzdálenosti v různých směrech. Proužky papíru či provázek pak můžeme použít i pro změření délky poloměru a obvodu. Mělo by nám vyjít, že obvod je vždy menší než \(2\pi\) krát příslušný poloměr. Můžeme se studenty provést i matematické odvození skutečného vztahu. Na obrázku 2 vpravo dole vidíme náčrtek řezu situace, kde můžeme využít eukleidovského poloměru \(r^\prime\) dané kružnice ukrytého uvnitř sféry. Jednoduchou geometrickou úvahou (vizte odvození vztahu 4.3 v kapitole 4.2 učebního textu) dojdeme k tomu, že mezi obvodem \(o\) kružnice na sféře a jejím sférickým poloměrem \(r\) platí \begin{equation*} o=2\pi R\sin\frac{r}{R}, \end{equation*} kde \(R\) je poloměr příslušné sféry. Na vztahu je například vidět, že pro dostatečně malé \(r\) v porovnání s poloměrem sféry můžeme využít aproximace \(\sin \frac{r}{R} \doteq \frac{r}{R}\) a vztah přejde na eukleidovskou verzi. Viděli jsme tedy, že naše vybraná geometrická tvrzení dopadnou na sféře jinak než v rovině. Ještě jednou připomeneme, že většinu těchto závěrů o geometrii na sféře můžete ukázat i na našem appletu.
 |
 |
 |
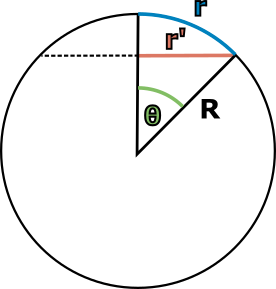 |
Obrázek 2 Praktické aktivity s geometrií na sféře. Vpravo dole: Náčrtek odvození vztahu obvodu kružnice na sféře a jejího sférického poloměru.
 |
 |
Obrázek 3 Applety ke sférické geometrii. Vlevo: Tento applet umožňuje mimo jiné pozorovat geodetický pohyb částic po sféře. Vpravo: Porovnání spojení dvou bodů o stejné zeměpisné šířce pomocí geodetiky a rovnoběžky.
Sféra je asi nejznámější zástupce plochy s tzv. kladnou křivostí. Slovo kladná zde souvisí s tzv. Gaussovou křivostí, což je veličina zaváděná v diferenciální geometrii. Počítá se v každém bodě plochy a v jistém slova smyslu popisuje míru zakřivení v daném bodě. My ji v našem povídání nebudeme potřebovat, takže se nebudeme zabývat její relativně složitou definicí. Poznamenejme jen, že na sféře o poloměru \(R\) vychází v každém bodě tato křivost jako \(1/R^2\), tedy jako kladné a zároveň na celé sféře stejné číslo. Jedná se tedy o plochu s konstantní kladnou křivostí. Že vychází křivost v každém bodě stejná není zas tak překvapivé, přece jen vypadá sféra v každém svém bodě stejně. Dále je na křivosti sféry vidět, že malý poloměr sféry znamená velké zakřivení a s čím dál tím větším poloměrem její zakřivení klesá.
Další plochy a křivosti
Pokud zbyde čas...
Existují i další čistě kladně zakřivené plochy. Příkladem je třeba elipsoid nebo paraboloid. Máme-li dostatek času, můžeme vyzkoušet, že tvrzení \eqref{2} dopadnou i na těchto plochách kvalitativně stejně jako na sféře. Jsou ale daleko těžší na vytvoření, než sféra. Velmi praktickou možností vytvoření těchto ploch je 3D-tisk. Máme-li k dispozici 3D-tiskárnu (a na školách už občas přeci jen jsou), je vytisknutí takových ploch vcelku hračka. V přehledu souborů na konci této stránky přikládám své STL soubory k tisku několika ploch. Druhou možností je vyrobit si takové modely sám, případně se studenty, například z kartónu, jak vidíme na fotkách v obrázku 3. U rotačních ploch je výroba založena na vkládání profilů z tvrdého kartónu do sebe. Kartónů se do sebe ale nedá zastrčit velké množství, tak abychom mohli s plochou opravdu pracovat a nebyla "děravá", přilepíme ke kartónu ještě za papíru vystřižené segmenty, jejichž tvar je napočítán tak, aby správně kopírovaly profil dané plochy. Celý princip je vidět na fotkách. Pro paraboloid jsou šablony na tyto výstřižky k dispozici v přehledu souborů, a časem přibydou i další plochy (tato kartónová výroba je ale spíše okrajová aktivita, máte-li tu možnost, rozhodně doporučuji 3D-tisk).
 |
 |
 |
Obrázek 4 Další příklady ploch s kladnou křivostí. Modely je možné vytisknout na 3D tiskárně nebo vyrobit z kartónu. Návrh postupu naznačují druhý a třetí obrázek. Příslušné soubory pro tisk jsou uvedeny na konci stránky.

Obrázek 5 Dvě geodetiky na válcové ploše vyslané stejným směrem udržují stále stejnou vzdálenost.
Asi nikoho nepřekvapí, že křivost v každém bodě roviny vychází nula. Jsou ale i jiné plochy s nulovou křivostí. Souvisí s tím otázka, kterou můžeme položit studentům: Co to vlastně znamená, že je nějaká plocha zakřivená? Typická odpověď bývá, že zakřivená plocha není rovná (tj. není rovina). My si ale můžeme ukázat, že, jak už jsme se zmínili, existují dva pohledy na věc - vnitřní a vnější geometrie. Nejlépe se to ukazuje na válcové ploše neboli plášti válce. I ten můžeme mít připravený předem, jak velký demonstrační, tak menší pro studenty. Já osobně válec s sebou nenosím, protože prakticky vždy dokážeme ve škole najít něco válcového. Velmi často jsou to odpadkové koše ve třídách, případně válcovou plochu dokážeme vytvořit čistě stočením listu papíru. A v tom spočívá ten vtip. Válcová plocha je z našeho vnějšího pohledu (tj. z pohledu 3D prostoru) zakřivená, má jistou vnější křivost. Na druhou stranu, kdybychom na ní vyzkoušeli tvrzení \eqref{2}, dopadnou úplně stejně jako na rovném listu papíru. Dá se to snadno dokázat právě tak, že například nakreslíme trojúhelník na list papíru a ten pak stočíme do válcové plochy. Vnitřní úhly v trojúhelníku musely zůstat stejné. Nakreslíme-li dvě rovnoběžky, po stočení mají stále všude stejnou vzdálenost (obrázek 5). To samé platí pro vztah obvodu a poloměru kružnice. Válcová plocha má vnitřní křivost stejnou jako rovina, tedy nulovou. Velmi jednoduchá a účinná zkouška je právě zkusit nějakou plochu obalit do listu papíru. Pokud se nám to povede, aniž bychom papír nějak potrhali nebo zpřehýbali (jako u válcové plochy), má stejnou vnitřní křivost jako list papíru, tedy nulovou. Například u koule by se nám to nikdy nepovedlo, mají odlišné vnitřní geometrie, a proto není například možné zabalit pomeranč do listu papíru, aniž bychom ho přehýbali či mačkali. To je například také důvod, proč není možné povrch Země zcela věrohodně přenést na papírovou mapu. Protože ale typicky nechceme nosit po kapsách glóbus, musí kartografové na mapách používat různá zkreslující zobrazení.

Obrázek 6 Brambůrky Pringles mají tvar hyperbolického paraboloidu.
Nyní se dostáváme i k záporně zakřiveným plochám. Příklad, kterým se budeme zabývat je tzv. hyperbolický paraboloid, nazývaný také sedlová plocha. Gaussova křivost všude na této ploše vyjde záporné, ale samozřejmě už ne konstantní. Na obrázku 7 vidíme, že tento název je docela trefný. Typicky ale nemáme k dispozici sedlo, které bychom mohli použít, takže si musíme pomoci jinak. Opět se nabízí 3D tisk (STL soubor je na konci stránky), případně vlastní výroba. Protože se již nejedná o rotační plochu, je kartónový model tvořen desíti navzájem zaklesnutými řezy (obrázek 7 vpravo) bez dodaného papírového povrchu, protože to už by bylo značně komplikované. Model by se dal samozřejmě udělat ještě hustší z více řezů, ale tato verze se ukazuje jako celkem dostačující na jednoduchou ukázku. Pro ozvláštnění a odlehčení s sebou na dílnu vždy přinesu brambůrky značky Pringles. Ne, že bych chtěl dělat reklamu konkrétní značce, ale tyto jako jediné mají tvar právě sedlové plochy (obrázek 6). Existují ještě levnější napodobeniny, které jsou ale jen části válcových ploch. Misku s brambůrky pošlu mezi studenty, každý si může tvar prohlédnout z blízka a nakonec ho sníst. Na větších modelech můžeme opět, i když už trochu pracněji, vyzkoušet tvrzení \eqref{2}. Například původně rovnoběžné trajektorie se zde rozcházejí (obrázek 7 vlevo). Podobně součet vnitřních úhlů v trojúhelníku bude menší než \(180^°\) a libovolná kružnice bude mít obvod větší než \(2\pi\) krát její příslušný poloměr na ploše (z časových důvodů se ale se studenty většinou omezím jen na tvrzení o rovnoběžkách, ze kterého je i trochu vidět tvrzení o úhlech v trojúhelníku). Vše dopadne "opačně" než u kladně zakřivených ploch. V tomto appletu si můžete vyzkoušet, jak vypadá geodetický pohyb na sedlové ploše. Dalším příkladem záporně zakřivené plochy je například rotační hyperboloid, který známe z chladicích věží některých elektráren.
Protože křivost je bodová vlastnost, existují samozřejmě i plochy, které mají oba druhy křivosti. Příkladem je třeba torus (tedy pneumatika) nebo třeba banán (který tak trochu připomíná kus torusu). Poznat se to dá často i na první pohled. Když se podíváme například na rozdíl mezi sférou a sedlovou plochou, vidíme, že sedlová plocha je prohnuta ve dvou navzájem kolmých směrech na opačné strany. Pokud si sféru představíme podobně rozříznutou ve dvou navzájem kolmých směrech, budou odhalená zakřivení "na stejnou stranu". V případě torusu je tohle přesně případ vnější strany. Představíme-li si ho ležícího na zemi, je v každém bodě na vnější straně ve vodorovném a svislém řezu zakřiven směrem do středu. Naopak, v libovolném bodě na vnitřní straně máme zatočení ve dvou různých směrech.
 |
 |
Obrázek 7 Další příklady ploch s kladnou křivostí. Modely je možné vytisknout na 3D tiskárně nebo vyrobit z kartónu. Návrh postupu naznačují druhý a třetí obrázek. Přislušné soubory pro tisk jsou uvedeny na konci stránky.
Pokud zbyde čas...
Poslední aktivitou této části, kterou si můžeme vyzkoušet, je ukázání souvislosti mezi kladnou a zápornou křivostí s pomocí šestiúhelníků (převzaté z [xiii]). Využijeme k tomu připravenou předpřipravenou kopii. Tu je třeba vystříhat kolem dokola a všechny naznačené přerušované čáry je třeba také prostřihnout. Zbyde nám tvar složený ze čtyř spojených "květin" s chybějícím šestiúhelníkem uprostřed (obrázek 8 vlevo). Pro ušetření času je dobré buď mít tvary už vystřižené, nebo požádat studenty, aby stříhali už během úvodu dílny. Nejprve vytvoříme model kladně zakřivené plochy. Všem asi bude znám fotbalový míč, který je tvořen pětiúhelníky, které jsou vždy obklopeny pěti šestiúhelníky. To nás bude inspirovat k tomu, že se pokusíme u každé "kytičky" jeden šestiúhelník schovat tak, že vždy dva sousední nastřižené do sebe zaklesneme. Výsledkem je přibližně část koule, tedy zjevně kladně zakřivená plocha. Abychom ji vytvořili, museli jsme oproti nezakřivené situaci "ubrat" materiál. Můžete tedy zkusit i obrácený postup. Pokud ke každé části přidáme jeden šestiúhelník, k čemuž slouží zvlášť vystřižené trojice šestiúhelníků (krajní šestiúhelníky slouží k zaklesnutí). Při troše šikovnosti brzy dostáváme výsledek, který se velmi podobá sedlové ploše (obrázek 8 vpravo dole).
 |
 |
 |
 |
Obrázek 8 Vlevo nahoře: Připravená kopie se šestiúhelníky. Vpravo nahoře: Fotbalový míč tvořen pětiúhelníky obklopenými šestiúhelníky. Vlevo dole: Model kladně zakřivené plochy "ubráním" šestiúhelníku. Vpravo dole: Model záporně zakřivené plochy vzniklý naopak "přidáním" šestiúhelníku.
Souvislost geometrie a gravitace (1 vyučovací hodina)
Nyní přišel čas vysvětlit si, jak souvisí naše dosavadní povídání o neeukleidovské geometrii a popis gravitace. Budeme se snažit poukázat na jistou podobnost mezi chováním trajektorií na zakřivených plochách a v přítomnosti gravitace. Ilustruje to obrázek 9. Představíme-li si těleso volně plující prázdným prostorem (tzn., nepůsobí na něj žádné síly nebo jsou všechny vyrovnány), bude se pohybovat podle 1. Newtonova zákona po přímce. Podobně, když se budeme hypoteticky pohybovat volně v rovině, bude naše trajektorie část přímky. Pokud se ale ocitneme v gravitačním poli, naše trajektorie se zakřiví. Podobně můžeme argumentovat v případě dvou těles, která se zpočátku pohybují rovnoběžně. Bez přítomnosti gravitace se budou pohybovat po stále rovnoběžných přímkách, v gravitačním poli se jejich trajektorie v závislosti na směru letu buď přiblíží nebo oddálí.
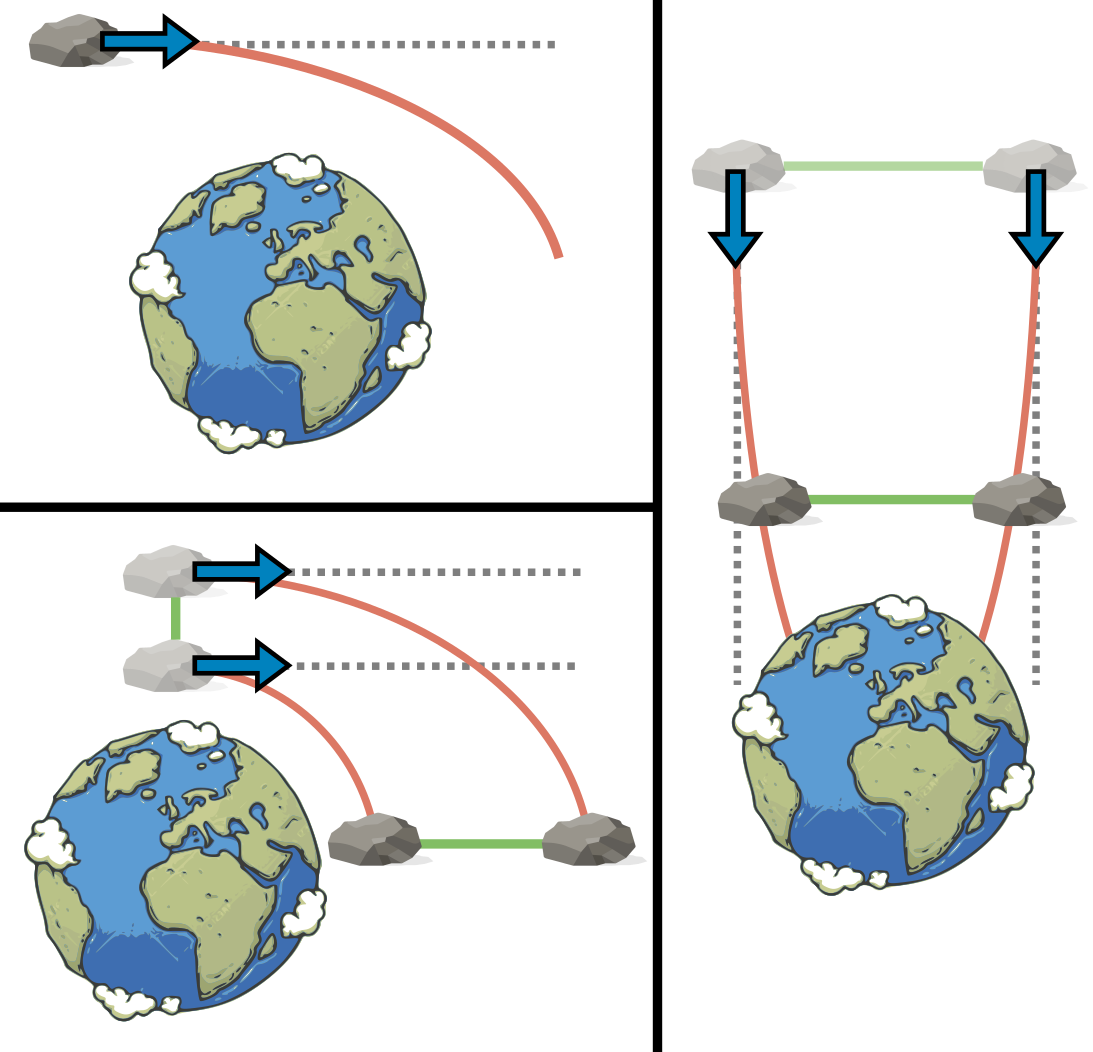
Obrázek 9 Vlevo nahoře: Trajektorie volně se pohybujícího se tělesa je přímka. Za přítomnosti gravitace je ale trajektorie zakřivena.
Vlevo dole a vpravo: Dva příklady situace, kdy vypustíme v gravitačním poli dvě tělesa rovnoběžnými směry. Bez gravitace by jejich trajektorie byly rovnoběžné přímky, za přítomnosti gravitace se tyto zpočátku rovnoběžné trajektorie k sobě přibližují či oddalují, podle směru vypuštění. V obou případech pouze upozorňujeme na jistou podobnost se zakřivenou geometrií. Netvrdíme, že dané chování je přesně stejné.
Se zakřivením ploch zde na první pohled ale úplně nevystačíme, protože gravitace existuje v prostoru. Zatímco zakřivenou plochu si dokážeme poměrně snadno představit jako vnořenou do třetího rozměru, představit si zakřivený prostor je nad naše schopnosti, a není snadné ho ani nějak vizualizovat. Přesto OTR přistupuje v přítomnosti gravitace k prostoru jako zakřivenému. Jak si to tedy máme představit? Podle mého názoru je nejlepším řešení nesnažit se o to. Člověka akorát rozbolí hlava a osobně pochybuji, že i zkušené relativisté či matematici si to umí představit. Řešením je spolehnout se na to, co již známe ze zakřivených ploch. Zakřivený prostor se bude od toho nezakřiveného (eukleidovského) lišit stejně jako se zakřivená plocha liší od roviny. Protože už se nemůžeme spolehnout na pohled zvnějšku, musíme se soustředit na vnitřní geometrii. I když se v zakřiveném prostoru bude nějaké těleso pohybovat neustále rovně, nebude jeho trajektorií přímka. Původně rovnoběžné trajektorie budou měnit svou vzdálenost, atd. Na druhou stranu, naštěstí se nám situace přece jen trochu zjednoduší. Pokud je zdroj gravitace sféricky symetrický, což je přiblížení, které se běžně ve školním prostředí používá a kterého se budeme držet i my (přece jen hvězdy a planety poměrně dobře sférické jsou), platí v klasické teorii gravitace i v OTR, že pohybující se těleso zůstává v rovině svého obíhání (známe to dobře z pohybu planet kolem Slunce, které jsou rovinné). Není třeba se studenty hned rozebírat zákon zachování momentu hybnosti. Stačí si nakreslit obrázek a rozmyslet si, že ve sférické symetrii nemá těleso důvod uhýbat mimo danou rovinu. V následujícím se tedy budeme věnovat rovinnému pohybu tělesa ve sféricky symetrickém gravitačním poli, což nám umožní některé věci názorně vizualizovat právě pomocí zakřivení této roviny do třetího rozměru.
Následující aktivita je velmi jednoduchá, ale mezi studenty poměrně oblíbená, a ilustruje jednu z nejzásadnějších myšlenek OTR. Můžeme ji najít například v [xiv]. Využijeme k ní další kopii. Jedná se o kuželovou plochu. Po vystřihnutí požádáme studenty, aby na ni narýsovali nebo načrtli rovnou čáru, procházející poměrně blízko prostředka, ale ne přímo skrz (obrázek 10 vlevo). Rovná čára pro nás představuje trajektorii volného tělesa v prostoru (ač omezeného na jednu rovinu) bez přítomnosti gravitace. Když bychom potom pomyslně zapnuli gravitaci, podle OTR se prostor v okolí gravitujícího tělesa, například hvězdy, zakřiví (jen rychle připomeňme, že čisté zakřivení prostoru není moc fyzikální a zanedlouho se dostaneme k zakřivení prostoročasu. Z didaktických důvodů ale zatím mluvíme pouze o prostorovém zakřivení). To budeme vizualizovat složením papíru do kuželové plochy ("papírové čepice"). Během toho vidíme, že zakřivením dané plochy se zakřivuje i "trajektorie" tělesa. Je ale velmi důležité dívat se na celou situaci správně. Začali jsme přímou trajektorií ve dvourozměrné rovině a celý pohyb stále v této původní rovině je. Naše zdeformování roviny do třetího rozměru je pouze za účelem vizualizace, není to tak, že by těleso díky gravitaci najednou opustilo původní rovinu. Proto se na celou situaci musíme dívat "shora" (obrázek 10 vpravo). Trajektorie tělesa je zakřivena, i když samo o sobě nijak nezatáčí. Podle OTR se pohybuje po geodetice v zakřiveném prostoru (i když jak už jsme upozorňovali, tohle je pravda jen z půlky, protože ve skutečnosti potřebujeme zakřivení prostoročasu, jedná se jen o koncepční mezikrok).

Obrázek 10 Vlevo: Model nezakřiveného prostoru s přímočarou trajektorií tělesa. Vpravo: V přítomnosti gravitace se podle OTR prostor zakřiví, což vede ke stočení trajektorie tělesa, přestože jde stále nejrovnější možnou cestou.
Všímavý student by mohl upozornit na jistý rozpor v našem povídání. Dříve jsme tvrdili, že každá plocha, kterou dokážeme pokrýt papírem bez jeho poničení, má nulovou křivost. To je ale i případ kuželové plochy. Až na její vrchol ji dokážeme snadno obalit do listu papíru, a dokonce ona je vlastně vytvořena z listu papíru, který se jen ohnul, takže jeho křivost by měla zůstat stále stejná. A je to skutečně tak, kuželová plocha má ve skutečnosti nulovou křivost všude kromě špičky, a v tom to právě je. Ve špičce je křivost nekonečně velká kvůli ostrému zlomu. Jedná se o singularitu. Jakákoli křivka, která dojde do špičky, nemá jednoznačný způsob, jak pokračovat dál. Pokud například povedeme dvě zpočátku rovnoběžné geodetiky tak, aby obě šly z jedné strany špičky kužele, bude jejich vzájemná vzdálenost stále stejná. Stejně jako v rovině nebo na válcové ploše. Pokud ale povedeme každou geodetiku z jedné strany špičky, protnou se podobně jako na sféře. Můžete si to vyzkoušet v příslušném appletu. Tato diskuze není nezbytně nutná pro zbytek dílny, ale rozhodně není od věci snažit se vyhnout vytváření nových miskoncepcí.
Pokud zbyde čas...
Aktivita s kuželem jde ještě propojit s předchozí částí o neeukleidovské geometrii. Z rovného listu papíru jsme vytvořili kuželovou plochu ubráním materiálu podobně, jako jsme to viděli u šestiúhelníků. Nevytvořili jsme sice kladně zakřivenou plochu v pravém slova smyslu, ale díky singulárnímu bodu uprostřed vykazuje jisté podobné vlastnosti. Pro vlastní potřebu bychom si ji mohli nazvat například pseudokladná plocha.
Můžeme si zkusit i opačný princip. Kopie obsahuje ještě druhou kruhovou výseč, jejímž připojením donutíme papír se zkroutit tak, že na první pohled poměrně dobře připomíná sedlovou plochu (obrázek 11). Opět je možné si vyzkoušet, že vyhýbáme-li se bodu uprostřed, jedná se stále o plochu s nulovou křivostí, ale zahrneme-li ho do oblasti, ve které si zkoušíme geometrii, budou se rovnoběžky rozcházet a i další testy dopadnou jako na záporně zakřivené ploše.

Obrázek 11 Vlevo: Přidáním kruhové výseče ke kuželové ploše vznikne plocha sice s nulovou křivostí, ale která díky singulárnímu bodu uprostřed může vykazovat znaky záporné křivosti.
Obrázek 12 Ilustrace k odvození univerzálnosti gravitačního působení.
Člověka jistě napadne otázka, proč se zrovna na gravitaci máme dívat jako na geometrii prostoru, a proč to neděláme u jiných běžně známých interakcí jako elektrická či magnetická síla? Odpovědí je, že gravitace má výsadní postavení díky své univerzálnosti. Narozdíl od elektrických a magnetických sil ji nejde odstínit. I na střední škole si ukazujeme, jak všem tělesům v daném místě způsobuje stejné zrychlení bez ohledu na jejich hmotnost. Předpokládejme, že máme gravitující těleso, například planetu, o hmotnosti \(M\) a malé testovací těleso o hmotnosti \(m\). Abychom našli zrychlení, které gravitace tělesu uděluje, stačí dosadit do Newtonova pohybového zákona \(F=ma\) a jako působící sílu dosadit tu gravitační ze vztahu \eqref{Newton}. Dostáváme \begin{equation}\tag{3}\label{3} ma=F_g=\frac{GmM}{r^2} \qquad \implies \qquad a=\frac{GM}{r^2}. \end{equation} Je ale potřeba zdůraznit, že vykrácení hmotností tělesa zde není samozřejmé. Málokdy se diskutuje o tom, že se nejedná o stejnou veličinu. Hmotnost vystupující v druhém Newtonově zákonu je tzv. setrvačná hmotnost, definována jako konstanta úměrnosti mezi působící silou a způsobeným zrychlením. Hmotnosti v gravitačním zákonu jsou něco jako "gravitační náboje" (v analogii s Coulombovým zákonem, kdy ve velmi podobném vztahu vystupují v čitateli elektrické náboje). Jedná se o vlastnost tělesa určující, jak moc na něj působí gravitační síla a také jak moc těleso gravitační silou působí na své okolí. Rovnost této gravitační hmotnosti a setrvačné není automatická a z ničeho přímo neplyne. V klasické mechanice je čistě přijímána jako fakt. Na druhou stranu, existuje celá řada historických i moderních experimentů, které tuto rovnost s čím dál vyšší přesností potvrzují. Jedním z výchozích principů OTR je právě tato rovnost, nazývaná slabý princip ekvivalence.
Slabý princip ekvivalence hrál zásadní roli ve vývoji a formulaci OTR, ale tomu se v naší dílně z nedostatku času věnovat nebudeme. Pokud vás zajímá více, můžete se více dozvědět v hlavním učebním textu. Pro nás je nejdůležitějším důsledkem slabého principu ekvivalence univerzálnost gravitačního působení. Pokud bychom ve vztahu \eqref{3} místo gravitační síly napsali známý Coulumbův zákon pro elektrickou sílu \(F_e\) mezi dvěma bodovými náboji \(Q_1\) a \(Q_2\) ve vzdálenosti \(r\) od sebe, nemá se hmotnost jednoho z nábojů ve vztahu pro zrychlení s čím vykrátit: \begin{equation}\tag{4}\label{4} ma=F_e=k\frac{|Q_1Q_2|}{r^2} \qquad \implies \qquad a=\frac{k}{m}\frac{|Q_1Q_2|}{r^2}, \end{equation} kde \(k\) je známá konstanta úměrnosti závislá na konkrétním prostředí. Pro nás důležité poselství tohoto výsledku je, že zrychlení udílené elektrickou silou závisí nejenom na zdroji elektrického pole a místě, ale i na částici/tělesu, které se urychluje, konkrétně na příslušném náboji a hmotnosti. Rozhodně tedy nemůžeme v tomto případě hovořit o nějaké univerzalitě elektrického působení. Abychom to shrnuli, formulovat náš přístup ke gravitaci pojmech něčeho tak univerzálně působícího, jako je samotná geometrie prostoru (prostoročasu), dává na rozdíl od jiných jevů smysl, protože gravitace se chová stejně. Poznamenejme ještě, že v této dílně neříkáme proč je přístup OTR geometrický. To je na jiné a ještě delší povídání (a snažíme se to osvětlit v učebním textu). My se v relativně krátkém čase snažíme ukázat a pokud možno názorně ilustrovat, jak vůbec relativistický popis gravitace vypadá, a co znamená.
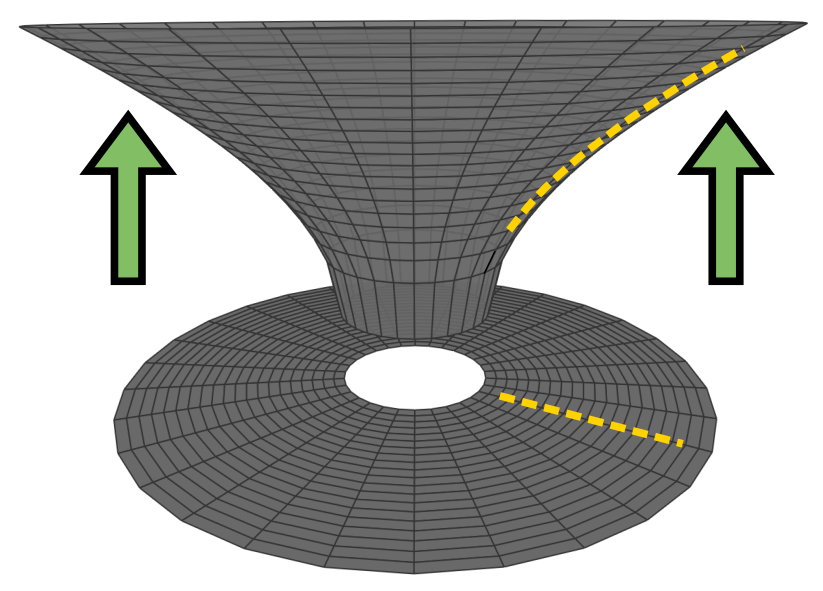
Abychom ale nezůstali jen u jednoduché aktivity s kuželem, podíváme se ještě na tzv. diagram vnoření. Jak jsme již řekli, zabýváme se zde tou nejjednodušší situací sféricky symetrického zdroje gravitace. Prostoročas kolem takového zdroje se nazývá Schwarzschildův a více se o něm můžete dozvědět v kapitole 4.3 učebního textu. Pro nás teď důležité, že existuje plocha, jejíž tvar je napočítán tak, aby vizualizoval prostorové zakřivení v ekvatoriální, neboli rovníkové rovině tohoto prostoročasu (tato volba konkrétní roviny není nijak limitující díky sférické symetrii celé situace). Se studenty nemusíme nutně jít takto do detailu. Je ale dobré říct, že tvar plochy, kterou si teď ukážeme, vychází z relativistických výpočtů a její zakřivení je stejné jako zakřivení předpovídané OTR v tomto symetrickém případě. Daná plocha se nazývá Flammův paraboloid a zájemci si mohou odvození jejího tvaru prohlédnout v příslušné podkapitole učebního textu.
Flammův paraboloid vidíme na obrázku 13 vlevo. Vznikne zakřivením ekvatoriální roviny do pomyslného třetího rozměru. Opět je třeba zdůraznit, že toto zakřivení je pouze vizualizační, nemá fyzikální význam a na případné trajektorie na ploše je třeba se dívat shora. Opět nejlepším způsobem, jak ho vyrobit, je 3D tisk (příslušný STL model je na konci stránky a kartónový model bude časem doplněn). Stejně jako v části o neeukleidovské geometrii můžeme se studenty prozkoumat vnitřní geometrii této plochy (například jako na obrázku 13 vpravo). Již by měli být také schopni říci, zda jde o kladně či záporně zakřivenou plochu. Opět máme k dispozici i applet, kde si můžete vyzkoušet posílání bodů po této ploše.
 |
 |
Obrázek 13 Vlevo: Vznik Flammova paraboloidu jako deformace ekvatoriální roviny tak, abychom zakřivení předpovídané OTR mohli pozorovat.
Vpravo: Vytištěný model s přiloženou papírovou geodetikou.
Tvar této plochy nám může být povědomý, protože je velmi typickou součástí vizualizací spojených s obecnou relativitou, zakřivením prostoročasu apod. Pravděpodobně také souvisí s často zmiňovaným přirovnáním prostoročasu za přítomnosti gravitace k elastické látce, která se prohne pod tíhou tělesa uprostřed. Demonstrace, kdy se po takové zakřivené ploše posílají kuličky jsou poměrně časté. V dílně se ale této aktivitě nevěnujeme, protože by si sama zasloužila celou vyučovací hodinu.
Nyní přichází důležitý bod v našem plánu. Buďto my, anebo v lepším případě někdo ze studentů musí upozornit na nedostatek našeho dosavadního modelu gravitace. Prostorové zakřivení, reprezentované Flammovým paraboloidem, umí demonstrovat, jak se trajektorie pohybujícího se objektu zakřiví. Pokud bychom ale nějaké těleso vypustili z klidu (tj. jen tak ho umístili na plochu paraboloidu), nemá důvod se začít pohybovat (reálnou gravitaci si v tomto případě musíme odmyslet, protože ta je představována zakřivením plochy). To znamená, že nedokážeme vysvětlit tak běžnou situaci, jako je volný pád. Jak už ale víme, je to proto, že pohled na gravitaci jako na zakřivení prostoru je neúplný. Například s pomocí něj nelze realizovat ani uzavřené orbity, což je něco, co zcela zjevně ve světě existuje, například u planet. Našemu popisu chybí ještě časová složka. Pojďme se tedy podívat "časové zakřivení" neboli gravitační dilataci času.
Gravitační dilatace času a systémy globální navigace (0,5 vyučovací hodiny)
Pokud jste se již seznámili s učebním textem, tato část bude prakticky stejná jako podobně nazvané podkapitoly. Namísto nějakého teoretizování začneme popisem reálného experimentu provedeného pány Hafele a Keatingem v 70. letech. Vzali několik velmi přesných atomových hodin na bázi cesia do letadla a obletěli s nimi svět směrem na východ a pak na západ. Čas uplynulý na hodinách byl po každém letu porovnán s atomovými hodinami, které zůstaly na zemi. V tabulce vidíme data převzatá ze stránky Wikipedie věnované tomuto experimentu:
| Tabulka 1 Naměřená data Hafeleova-Keatingova experimentu, zdroj: Wikipedia | ||||
|---|---|---|---|---|
| Předpovězený rozdíl v \(\text{ns}\) | ||||
| Gravitační efekt | Kinematický efekt | Celkem | Naměřeno / \(\text{ns}\) | |
| Východní směr | \(+144±14\) | \(-184±18\) | \(-40±23\) | \(-59±10\) |
| Západní směr | \(+179±18\) | \(+96±10\) | \(+275±21\) | \(+273±7\) |
V tabulce si můžeme všimnout hned několika zajímavostí. Za prvé se během experimentu uplatňuje nejen gravitační dilatace času, ale i ta kinematická, tj. ta způsobená vzájemným pohybem, kterou jsme se zabývali ve speciální relativitě. Letadla byla pochopitelně nejenom v jiné nadmořské výšce, ale také se musela nutně vůči hodinám na zemi pohybovat. Obě dilatace samozřejmě ovlivňují chod hodin najednou, ale v přímém měření je nedokážeme nijak rozlišit. V tabulce vidíme, že autoři experimentu odhadli z teorie velikost obou efektů a pak jejich vliv sečetli. Všimněme si také, že zatímco gravitační efekt je pro oba směry letu podobný a souvisí s nadmořskou výškou letů, kinematický efekt se výrazně liší. Je to dáno skládáním rychlostí, protože nezapomeňme, že se vše odehrálo na rotující Zemi. Letět na východ znamená letět ve směru rotace Země, takže pokud chcete obletět planetu, musíte se pohybovat rychleji, než se pohybuje povrch Země. Při cestě na západ, tedy proti směru rotace, je to prakticky naopak. Letadlo stojící na ranveji se už pohybuje společně s rotující Zemí, takže pokud letíme na západ, prakticky zpočátku jen zpomalujeme vůči povrchu. Je to podobné, jako když chcete hodit míčem ve vlaku. Házíte-li ve směru pohybu, musí se míč chvíli vůči zemi pohybovat rychleji než vlak. Hodíte-li ho proti směru pohybu, je klidně možné, že se vůči zemi bude stále pohybovat stejným směrem jako vlak, jen pomaleji, takže ho vlak předběhne. Samozřejmě je možné hodit (čí spíše už vystřelit) míč směrem proti pohybu vlaku rychleji, než se vlak pohybuje, v tom případě se bude míč pohybovat i vůči zemi na opačnou stranu.
Poslední dva sloupce tabulky ukazují porovnání předpovězených hodnot s těmi naměřenými. Dobrou shodu vidíme zejména v případě pohybu západním směrem, ale i v případě toho východního se intervaly nejistoty překrývají, což poukazuje na, sice ne příliš přesnou, ale přece jen shodu mezi teorií a experimentem. Od té doby se uskutečnilo hned několik dalších podobných experimentů, které také potvrdily správnost relativistických predikcí se stále větší přesností.
Poznamenejme na téma experimentů ještě jednu zajímavost. Doba od Hafeleova-Keatingova experimentu pokročila a s ní i přesnost, které atomové hodiny dosahují. V roce 2010 se týmu z amerického Institutu standardů a technologií podařilo s využitím nové generace atomových hodin využívajících ionty hliníku (s přesností řádu \(10^{-17}\), to mimo jiné znamená, že tyto hodiny se díky akumulující se chybě „rozejdou“ o \(1\:\text{s}\) nejdříve za \(10^{17}\:\text{s}\), což odpovídá přibližně deseti miliardám let) změřit relativistickou dilataci času u dvojice hodin, které se vůči sobě pohybovaly relativní rychlostí \(10\: \text{m/s}\) (ve skutečnosti se vůči sobě pohybovaly hliníkové ionty v hodinách, ale to je jen technický detail), případně které dělila vertikální vzdálenost \(33\:\text{cm}\). A naměřené hodnoty byly opět ve shodě s relativistickou předpovědí. Odkaz na původní vědecký článek můžete najít v seznamu literatury pod [vii]. Vývoj ale mezitím stále pokračuje, a tak byla v roce 2021 potvrzena gravitační dilatace času na vzdálenost \(1\:\text{mm}\)! Dnes už tedy dokážeme naměřit relativistické jevy v situacích, které běžně zažíváme, nejen při pohybu rychlostí blízkou rychlosti světla nebo v okolí neutronových hvězd či černých děr. Můžete tedy směle tvrdit, že z fyzikálního hlediska je vaše hlava starší než vaše nohy.
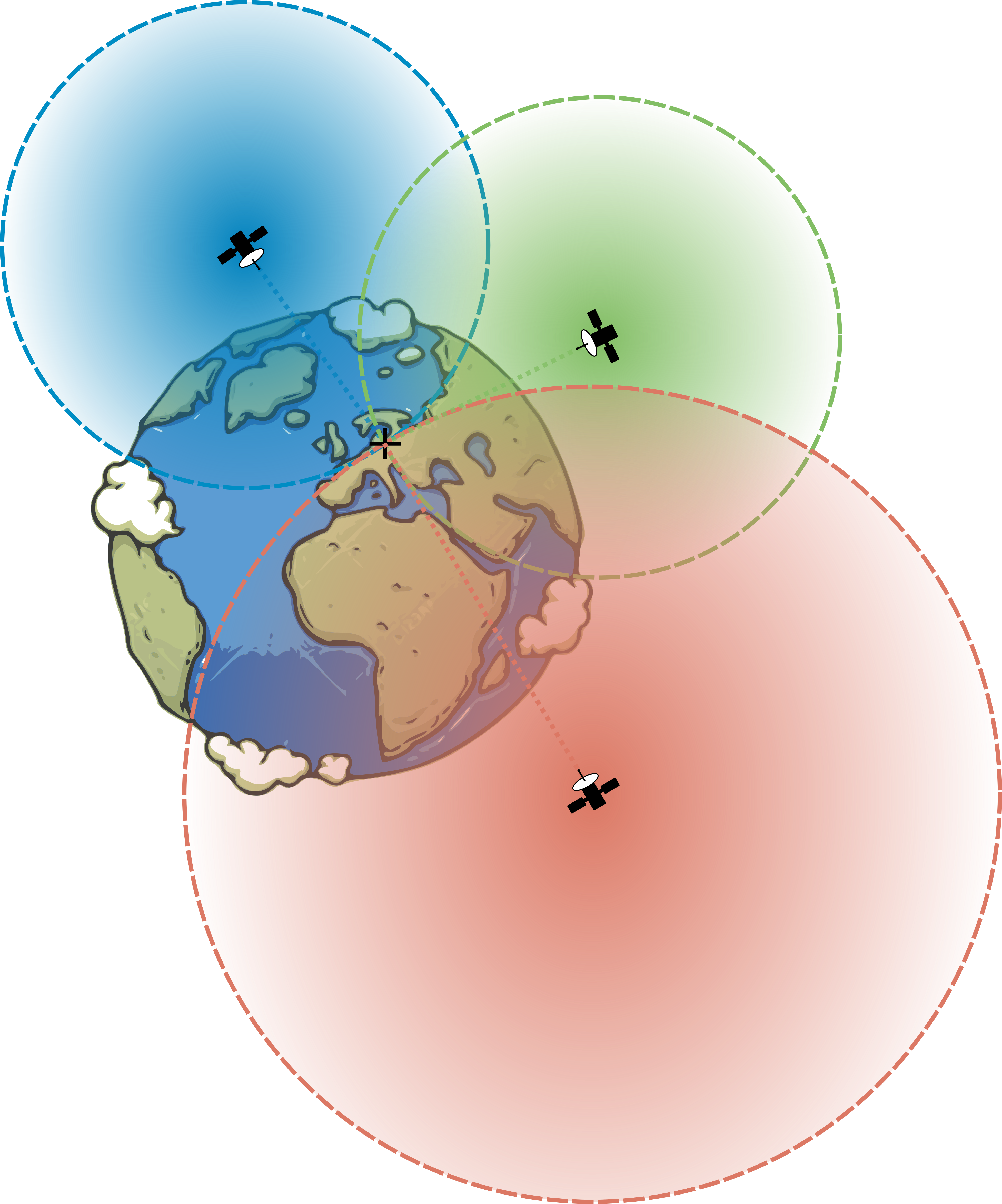
Obrázek 14 Zjednodušený model fungování globálního satelitního navigačního systému.
Aby ale nezůstalo jen u teoretického výkladu, zkusíme si i něco spočítat. Dilatace času hraje totiž zásadní roli v satelitních systémech globální navigace, kterými určujeme naší polohu. Nejprve je dobré si shrnout, jak takové systémy fungují. Způsobu, jakým telefony a jiná zařízení určují naši polohu, se někdy ne zcela správně říká GPS (z anglického Global Positioning System), ale to je ve skutečnosti název jen jednoho z několika existujících samostatných systémů. Americký GPS byl první, ale dnes existuje i ruský GLONASS, evropský Galileo nebo čínský BeiDou. Podpůrné či regionální systémy má i Japonsko (QZSS) a Indie (IRNSS). Komerční navigační zařízení ale často nejsou omezena na využívání jen jednoho z těchto systémů a běžný uživatel stejně typicky nepozná, který je jeho zařízením využíván. Souhrnně mluvíme o tzv. systémech globální satelitní navigace (GNSS – z anglického Global Navigation Satellite System, aby těch zkratek nebylo málo). Všechny jsou založeny na stejném principu. Sestávají z celé flotily satelitů obíhajících naši planetu. Každý ze satelitů má na palubě atomové hodiny a jeho úkolem je v pravidelných intervalech vysílat údaj o aktuálním čase a své poloze. Naše polohovací zařízení pak zachytí signály satelitů, které jsou „na dohled“, a z rozdílu časů mezi odesláním signálu a jeho přijetím, za předpokladu, že se signál pohybuje rychlostí světla, vypočítá vzdálenost, jakou se nacházíme od satelitu jednoduše jako \(\Delta s=c\Delta t\). Musíme se tím pádem nacházet někde na sféře o poloměru \(\Delta s\) se středem ve sdělené poloze satelitu. Abychom pak určili naši polohu, potřebujeme teoreticky informace alespoň ze tří satelitů (obrázek 14). Tyto tři sféry se sice mohou obecně protínat ve dvou různých bodech, ale přidá-li se informace o tom, že se nacházíme na Zemi a ne někde ve vesmíru (či na které polokouli se zrovna nacházíme), řešení je už jednoznačné. Alespoň teoreticky, prakticky jsou díky nejistotě měření vyžadovány informace z více satelitů, čímž se zvětšuje přesnost určení naší polohy. Tím ale komplikace nekončí, náš popis je samozřejmě jen velmi zjednodušenou verzí velmi sofistikovaného technického řešení. Nahlédneme-li do technicky orientovaných článků [viii,ix] či příslušné stránky Wikipedie, zjistíme, že skutečnost je daleko složitější a inženýři navrhující navigační systémy musí pracovat také s rotací Země, vlivem atmosféry na šíření signálu apod. Navíc, jak uvidíme později, pro určení polohy s přesností alespoň na metry by naše zařízení muselo umět měřit čas s přesností přinejmenším na desítky nanosekund. To ale naše mobilní a jiná navigační zařízení typicky nedokáží a musí jim být dodávána i časová informace. Máme tedy o jednu neznámou navíc, takže ve skutečnosti je vyžadován signál ne od tří ale minimálně od čtyř satelitů. My se samozřejmě do takových technických detailů pouštět nebudeme, ale je dobré si uvědomit, že skutečnost je o mnoho složitější než náš jednoduchý výklad.
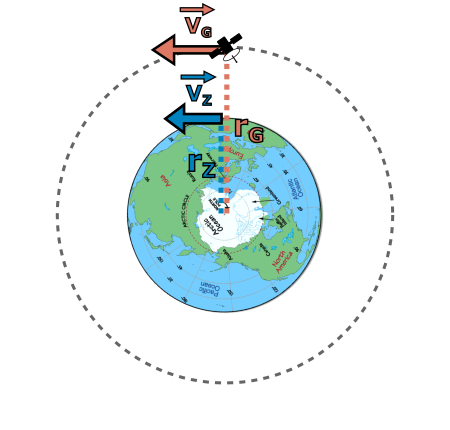
Obrázek 15 Náčrtek k příkladu se systémem globální navigace. Stojíme na povrchu Země v oblasti rovníku, takže se pohybuje příslušnou obvodovou rychlostí země \(\vec{v}_\text{Z}\) a naše vzdálenost od středu je samozřejmě poloměr Země \(r_\text{Z}\). Podobně navigační satelit obíhá rychlostí \(\vec{v}_\text{G}\) na kruhové dráze o poloměru \(r_\text{G}\).
Asi už chápete, kde do hry vstupuje relativita. Z dříve řečeného plyne, že čas na oběžné dráze satelitů plyne jinak než nám na povrchu Země, což je problém, když využíváme rozdíly časů k měření vzdálenosti. Ukažme si nyní na jednoduchém výpočtu, jaké chyby bychom se s využitím navigace dopustili, pokud bychom neznali relativitu. Vezměme si zjednodušenou situaci, kdy stojíme na rovníku (poloměr \(r_\text{Z}\)) a chceme porovnat chod času na našich hodinách (označme \(\Delta t_\text{Z}\)) a na hodinách umístěných v satelitu navigačního systému Galileo \(\Delta t_\text{G}\), který kolem Země obíhá po přibližně kruhové dráze o poloměru \(r_\text{G}\) (obrázek 15). Nejsme nyní v pozici, kdy bychom při naší krátké exkurzi od základů OTR mohli odvodit nějaký vzorec. Nutně nám budou muset spadnout shůry. Naštěstí nebudou nijak složité. Lze odvodit (a to odvození najdete v učebním textu), že chceme-li porovnávat plynutí času dvou statických pozorovatelů stojících na zmíněných poloměrech, dostáváme \begin{equation}\tag{5}\label{5} \frac{\Delta t_\text{Z}}{\Delta t_\text{G}}=\frac{\sqrt{1-\frac{2GM}{c^2r_\text{Z}}}}{\sqrt{1-\frac{2GM}{c^2r_\text{G}}}}=\frac{\sqrt{1-\frac{r_\text{S}}{r_\text{Z}}}}{\sqrt{1-\frac{r_\text{S}}{r_\text{G}}}}. \end{equation} Ve vzorci vystupuje několik konstant, Newtonova gravitační konstanta \(G\), hmotnost centrálního tělesa, v jehož gravitačním poli se nacházíme, \(M\), a rychlost světla ve vakuu \(c\). Kombinace těchto konstant \(2GM/c^2\equiv r_\text{S}\) se vyskytuje v relativitě tak často, že má svůj vlastní název a označení. Jmenuje se Schwarzschildův poloměr, a je vidět, že je plně dána hmotností daného centrálního tělesa. Například pro Zemi vychází tento poloměr přibližně \(8{,}87\:\text{mm}\). Toto číslo mimojiné znamená, že pokud bychom chtěli ze Země vytvořit černou díru, museli bychom její hmotu stlačit do kuličky s tímto poloměrem či menším. Jen pro zajímavost, pro Slunce vychází \(r_{S}\) zhruba \(3\:\text{km}\), v obou případech se jedná o vzdálenosti výrazně menší, než jsou rozměry těchto objektů, takže se nemusíme bát, že by se z nich staly samy o sobě černé díry.
Vztah \eqref{5} ale není pro nás zcela ten správný, protože platí pro statické pozorovatele. Chceme-li porovnávat plynutí čas nás na povrchu planety a satelitu obíhajícího na oběžné dráze, musíme si uvědomit, že jak satelit, tak i my se pohybujeme (v našem případě je to díky rotaci Země). Zde na nás musí na chviličku vyskočit speciální relativita. Studenti mohou a nemusí vědět, že už ve speciální relativitě existuje dilatace času dána vzájemným pohybem. Chody našich hodin jsou tedy v tomto případě ovlivněny nejenom různou nadmořskou výškou, ale i naším vzájemným pohybem. Nebudeme se opět zabývat odvozováním (opět ho najdete v učebním textu) a pokud uznáte za vhodné, můžete studentům rovnou přednést finální vzorec místo předchozího (osobně mi ale připadá lepší mezikrok vzorce pro statické pozorovatele). Nicméně v případě rovnoměrných pohybů po kružnici obou pozorovatelů s příslušnými rychlostmi \(v_\text{Z}\) a \(v_\text{G}\) se vztah \eqref{5} změní na \begin{equation}\tag{6}\label{6} \frac{\Delta t_\text{Z}}{\Delta t_\text{G}}=\frac{\sqrt{1-\frac{r_\text{S}}{r_\text{Z}}-\frac{v_\text{Z}^2}{c^2}}}{\sqrt{1-\frac{r_\text{S}}{r_\text{G}}-\frac{v_\text{G}^2}{c^2}}}. \end{equation} Znalcům speciální relativity mohou být členy \(v^2/c^2\) pod odmocninami povědomé, podobné vystupují totiž ve vztazích speciální relativity. Není to tak, že bychom nějak oba vzorce "lepili" dohromady. Ono to tak prostě vyjde. Je to taková malá ukázka faktu, že OTR je nadstavbou STR, obsahuje ji v sobě. Všechny relevantní parametry výpočtu je možné snadno dohledat na internetu. Za poloměr Země můžeme vzít známou hodnotu \(6378\:\text{km}\) a u systému Galileo najdeme oběžnou dráhu přibližně \(29600\:\text{km}\). Můžeme si se studenty připomenout vztahy známé pro kruhový pohyb a ze znalosti periody a poloměru vypočítat příslušné kruhové rychlosti. Perioda oběhu Země je samozřejmě 24 hodin a pro satelit činí 14 hodin. Celkem nám vyjde rychlost oběhu na povrchu Země cca \(464\:\text{m}\cdot\text{s}^{-1}\) a u satelitu \(3675\:\text{m}\cdot\text{s}^{-1}\). Konečně můžeme do našeho vztahu dosadit. Respektive ho využijeme, abychom spočítali relativní odchylku časů uplynulých pro nás na povrchu Země a pro satelit: \begin{align*} \frac{\Delta t_\text{G}-\Delta t_\text{Z}}{\Delta t_\text{G}}=1-\frac{\Delta t_\text{Z}}{\Delta t_\text{G}}=1-\frac{\sqrt{1-\frac{r_\text{S}}{r_\text{Z}}-\frac{v_\text{Z}^2}{c^2}}}{\sqrt{1-\frac{r_\text{S}}{r_\text{G}}-\frac{v_\text{G}^2}{c^2}}}=1-\frac{\sqrt{1-\frac{8{,}8\cdot10^{-3}}{6378\cdot10^3}-\frac{464^2}{9\cdot10^{16}}}}{\sqrt{1-\frac{8{,}8\cdot10^{-3}}{29600\cdot10^3}-\frac{3675^2}{9\cdot10^{16}}}}\dot{=}\:4{,}67\cdot10^{-10} \end{align*} Tento výsledek znamená, že zatímco hodinám v satelitu uplyne \(1\) sekunda, na Zemi nám uplyne o zhruba půl nanosekundy méně. Nezdá se to jako moc, ale je to již měřitelný rozdíl. Předně si ale musíme uvědomit, že tato nepřesnost se s každou sekundou kumuluje. Za celý den činí časový rozdíl asi \(40\) mikrosekund. Když si pak vzpomeneme, že navigační systém pomocí rozdílu časů vyslání a přijetí určuje naši vzdálenost od satelitu, odpovídá to přibližně chybě v určení vzdálenosti \(\Delta s=c\Delta t=3\cdot 10^8\cdot40\cdot 10^{-6}\:\text{m}=12000\:\text{m}\). Pokud bychom neznali relativitu, systém globální navigace by se za jeden den rozešel s realitou o \(12\:\text{km}\) při určování vzdálenosti od nás k satelitům, a tím pádem by vznikla chyba i v určení naší polohy. Relativistické efekty jsou tedy v okolí Země sice malé, ale satelitní navigační systémy musí měřit čas s takovou přesností, že se zde relativita již jasně projevuje.
Traduje se, že když byl ve Spojených státech v 70. letech minulého století vyvíjen systém GPS, byla sice už teorie relativity fyzikům známa, ale inženýři navrhující systém v ní neměli velkou důvěru. Proto byly sice do satelitů naprogramovány potřebné relativistické korekce, ale byly zpočátku vypnuty s možností je dálkově zapnout. Po úvodním spuštění začala přesnost systému postupně degradovat, což napravilo až zapnutí zabudovaných korekcí. Až se vás tedy někdy někdo zeptá, k čemu je ta relativita vlastně dobrá, zeptejte se jich na oplátku, kdy naposled používali mapy s globální navigací.
Zakřivení prostoročasu (0,5 vyučovací hodiny)
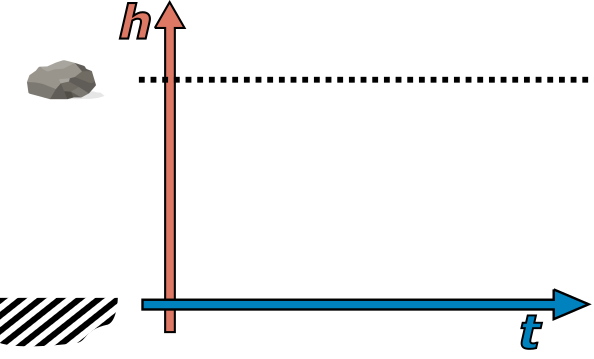
Obrázek 16 Při „vypnuté“ gravitaci se výška kamene s časem nemění. Jejím grafem je tedy konstantní funkce.
Nyní se konečně dostáváme k tomu volnému pádu. Vezměme si velmi jednoduchou situaci, kdy máme kámen v klidu v nějaké počáteční výšce nad zemí. V rámci našeho myšlenkového experimentu prozatím vypneme gravitaci, takže kámen stojí nehybně ve vzduchu. Zkusme si nyní nakreslit graf závislosti výšky kamene nad zemí – označme ji \(h\) - na čase, tedy \(h(t)\). Jelikož se prozatím výška nijak nemění, mělo by se pochopitelně jednat o graf konstantní funkce (obrázek 16). Graf závislosti nějaké veličiny prostorového charakteru (v našem případě výšky) na čase pro nás snad není nic neobvyklého. Možná vás ale překvapí, že jsme právě načrtli jednoduchý případ tzv. prostoročasového diagramu (ten se sice v relativitě konvenčně kreslí s časovou osou svisle, ale to na věci nic nemění), kde jeden rozměr reprezentuje čas a druhý prostor (pro jednoduchost omezený jen na jednu prostorovou dimenzi, abychom nemuseli „kreslit“ tří- či čtyřrozměrné obrázky – i kdybychom to uměli). Takové diagramy se kreslí zejména už ve speciální relativitě, ale my jsme ho až dosud k ničemu nepotřebovali.
Pokud by měly obě osy v grafu prostorový význam, například souřadnice \(x\) a \(y\), tedy konvenčně vodorovná a svislá vzdálenost, křivka grafu by odpovídala trajektorii tělesa v prostoru. Analogicky odpovídá v případě prostoročasové diagramu zobrazená křivka trajektorii v prostoročasu, tzv. světočáře. Prakticky řečeno obsahuje informaci, jak se těleso pohybuje v prostoru a jak mu plyne čas (jinými a trochu návodnými slovy: jak se pohybuje v čase).
Světočára kamene na obrázku 16 je přímka, podobně jako je přímkou trajektorie volné částice v prostoru. Je to proto, že situace bez gravitace odpovídá plochému (tj. nezakřivenému) prostoročasu – přesně tomu, jaký jsme popisovali v části o speciální relativitě. Když nyní pomyslně „zapneme“ gravitaci, prostoročas se zakřiví. Celá situace je nyní analogická aktivitě na obrázku 4.21, kdy jsme účinek zakřivení na trajektorii tělesa demonstrovali složením papírové plochy do pláště kužele. Rozdíl je v tom, že nyní nezakřivujeme čistě prostor a tím prostorovou trajektorii tělesa, nýbrž prostoročas a tím pádem jeho světočáru. Abychom mohli tuto zásadní myšlenku celého našeho povídání demonstrovat, potřebujeme zakřivit i náš prostoročasový diagram. Můžeme ho tedy nakreslit na povrch, o kterém víme, že je jeho vnitřní geometrie odlišná od listu papíru.

Obrázek 17 Demonstrace zakřiveného prostoročasového diagramu. Světočára tělesa je geodetikou – tedy nejpřímější možnou "trajektorií" v zakřiveném prostoročase. Kámen se tím pádem nutně dostává na nižší výšku – padá.
To je například naše stará známá sféra, anebo, jak už víme, jakákoli sféře podobná plocha. Jeden konkrétní příklad vidíme na obrázku 17. Zde jsme na povrch nafouknutého balónku předkreslili osy prostoročasového diagramu. Na zakřiveném balónku samozřejmě nemůžeme realizovat souřadnicové osy jako vzájemně kolmé přímky, ale už víme, že zobecněním přímky je geodetika, kterou jsme na plochách napodobovali pomocí provázku nebo pruhu papíru. Osy pro nás tedy budou části dvou geodetik, které se v jednom místě potkávají pod pravým úhlem (na pomyslné zeměkouli by se mohlo například jednat o část rovníku a poledníku). Na svislé ose pak ještě vyznačíme počáteční výšku kamene. Jeho světočáru tělesa jsme našli také jako geodetiku na povrchu pomocí proužku papíru. Proč jako geodetiku? Protože vše, co jsme si říkali u zakřivení ploch a prostoru platí stále, jen se posouváme o dimenzi výše. Geodetiku jsme zavedli fyzikálně jako trajektorii tělesa na zakřivené ploše, pokud na těleso nepůsobí žádné vnější síly. To znamená, že se pohybuje stále „rovně“, a jakákoli změna jeho pohybu je dána čistě geometrií dané plochy. V zakřiveném prostoru byly naše úvahy naprosto stejné, jen jsme se místo dvourozměrné zabývali třírozměrnou situací. Přechod z prostoru na prostoročas je podobný. V nezakřiveném prostoročase je „trajektorií“ tělesa přímka. V zakřiveném prostoročase je to zakřivený ekvivalent přímky – tedy geodetika. Zakřivení prostoročasu tedy způsobilo i zakřivení světočáry kamene. Výsledkem je, že se kámen dostává na nižší výšku. Začal sám od sebe padat a to pouze díky svému zakřivenému „pohybu“ v prostoročase. Žádné těleso ani částice totiž nemůže v prostoročase "stát na místě" už jen díky tomu, že existuje, a tím pádem pro něj plyne čas. Takže i když pak třeba stojí v klidu v prostoru, v prostoročase má nějakou trajektorii vždy.
Nyní je náš popis gravitace, alespoň po kvalitativní stránce, kompletní. Pojďme si to tedy shrnout. Začali jsme neslučitelností speciální teorie relativity a klasické teorie gravitace a dospěli jsme k tomu, že gravitaci můžeme vysvětlit, pokud se na prostoročas v přítomnosti gravitace budeme dívat jako zakřivený, tedy aplikujeme na něj stejný matematický popis, jaký se používá například u zakřivených ploch. Rozdíl je v tom, že u ploch máme dvě prostorové souřadnice a v prostoročasu máme souřadnice čtyři – tři prostorové a jednu časovou. A protože to je poměrně velký koncepční krok, vzali jsme to postupně, ze dvou souřadnic jsme přešli na tři – k zakřivenému prostoru. Ukázalo se ale, že to nestačí. Museli jsme přidat právě i časovou složku, aby byl náš popis úplný. Tím jsme dospěli k již avizované základní myšlence obecné relativity: „Gravitace je zakřivení prostoročasu.“
Samozřejmě o obecné relativitě je možné toho říci ještě spoustu, rozhodně je zajímavé mluvit o historických i současných experimentech, které zatím všechny souhlasí s předpověďmi OTR. Ty nejzásadnější jsou popsány v učebním textu v kapitole 4.3. Pokud by se studenti chtěli dozvědět o relativitě více podrobností, například proč se dívá na gravitaci jako na zakřivení prostoročasu, budu rád, když je odkážete na učební text na této stránce. Na závěr bych ještě rád připomněl, že budu rád za jakékoli připomínky či dotazy k této dílně. Pokud ji chcete sami vyzkoušet se studenty a chtěli byste se o tom poradit, určitě napište. A pokud dílnu zrealizujete, budu určitě rád za vaše zkušenosti.
Matěj Ryston: matej.rys gmail.com
gmail.com
Soubory ke stažení
Papírové kopie
STL soubory pro 3D tisk:
Kartónové modely
- Paraboloid profil - obkreslit 4x na kartón
- Výstřižky pro povrch paraboloidu - vytisknout 2x pro jeden model
- Sedlová plocha - 1/3
- Sedlová plocha - 2/3
- Sedlová plocha - 3/3