Část 3: Speciální relativita
I když byly první články o speciální teorii relativity publikovány Albertem Einsteinem v roce 1905, aby byl náš popis úplný, konkrétně, abychom odpověděli i na otázku Proč?, a ne jenom Jak?, musíme se podívat o něco dále do minulosti. Naše historická vsuvka bude ale velmi stručná, protože tento text nemá za cíl se zabývat historií vědy. Abychom ale uspokojili poznáníchtivého čtenáře, uvádíme alespoň odkazy na doporučenou literaturu.
Když James Clerk Maxwell (1831 - 1879) předvedl světu své rovnice elektromagnetismu, mimo jiné z nich vyplynulo, že změny elektrického a magnetického pole se svázány dohromady šíří prostorem rychlostí světla jako vlna. Pro mnohé to byl poslední kousek skládačky v mnohaleté snaze o odhalení povahy světla. Ona totiž otázka „Co je světlo?“ hlodala lidem v hlavách již dlouho. Již od začátku 18. století díky Youngovu pokusu převažoval názor, že světlo je vlna. Ale vlna čeho? A najednou Maxwellovy rovnice jasně ukazovaly, že světlo nejenže skutečně vlna je, ale je to vlna elektromagnetická. Více podrobností se můžete dočíst například v anglicky psané knize [i].
Obrázek 3.1 Ilustrace spektra EM vlnění. Obrázek převzat ze stránky fyzweb.cz
Jak už to tak bývá, po jedné odpovědi přišlo daleko více otázek. Ta patrně nejzásadnější by šla zformulovat takto: „Jestliže světlo je vlna, co se tedy doopravdy vlní? Když hodím kámen do vody, zvlní se vodní hladina, když mluvím, zvuk se šíří prostorem jako tlakové vlny ve vzduchu. Co je tedy to médium, které se vlní, když se šíří světlo?“
Hypotetická látka, která svým kmitáním umožňuje šíření světla prostorem, byla nazvána éter (z řeckého aether). Jestliže je vše průhledné vyplněno éterem (včetně vesmírného vakua) a Země obíhá kolem Slunce, zdá se být celkem logické, že bychom v různých směrech měli naměřit různou rychlost světla. Proč? Vraťme se opět k analogii s vodní hladinou. Pokud se budeme plavit na lodi a budeme pozorovat vlny, které k nám přicházejí, jejich rychlost vůči nám bude záviset na směru, ze kterého přicházejí. Vlnám přicházejícím ze směru přídě pojedeme naproti, proto i jejich rychlost vůči nám bude větší než oproti vlnám přicházejícím od zádi, protože těm naopak ujíždíme. Opět se dostáváme ke skládání rychlostí ve dvou inerciálních soustavách, vodní hladiny a rovnoměrně přímočaře se pohybující lodi. V této analogii je Země naše loď, na které se (hypoteticky) plavíme éterem (s tím rozdílem, že Země se striktně řečeno nepohybuje rovnoměrně přímočaře, ale můžeme si představit, že po dostatečně krátký čas to přibližně platí). Situace se světlem je navíc o to komplikovanější, že na rozdíl od vody nemůžeme éter přímo pozorovat. Dokážeme změřit pouze rychlost světelných vln.
Při pokusech s měřením rychlosti světla ve směru pohybu Země a kolmo na něj, s nimiž jsou nejvíc spojována jména pánů Alberta Michelsona (1852 - 1931) a Edwarda Morleye (1838 - 1923), se nepodařilo najít rozdíly v rychlosti světla měřené v různých směrech. Tento výsledek začal podrývat některé základní principy fyziky. Člověk by například čekal, v souhlasu s éterovou teorií a především s Galileiho transformací a z ní plynoucím skládáním rychlostí, že pokud se auto pohybuje rychlostí \(v\) vůči éteru a z jeho reflektorů vychází světlo rychlostí \(c\) vůči éteru, tak se bude prostorem šířit vzhledem pozorovateli v autě rychlostí \(c-v\). Experimenty ale mluvily proti této možnosti. Zdál se tu být tím pádem jistý rozpor mezi klasickou mechanikou a elektromagnetismem, kterým popisujeme mimo jiné i šíření světla.
Mimochodem, už jsme naznačovali, že základní pohybová rovnice mechaniky je invariantní vůči Galileiho transformaci. Již zmíněné Maxwellovy rovnice elektromagnetismu, jejichž podoba je bohužel opravdu na rámec tohoto textu, vůči ní invariantní nejsou. To je právě matematický důsledek rozporu mezi klasickou mechanikou a elektromagnetismem.
Bylo zformulováno několik fyzikálních teorií, které se snažily toto chování přírody vysvětlit (vizte [i], rozsáhlý rozbor historie vzniku speciální relativity a konkurenčních teorií je uveden na anglické Wikipedii), ale žádná nedosáhla obecnějšího uznání, případně neobstála při porovnání s experimenty. Až pak Einsteinův článek z roku 1905 přinesl počátek speciální teorie relativity, která na základě několika málo předpokladů dokázala vysvětlit zmíněné experimenty, a to přímočařeji a přirozeněji než jiné teorie. Znamenala tak konec úvah o éteru.
Ucelenější a detailnější popis historického vývoje vedoucího k formulaci STR lze nalézt v doporučené literatuře (v češtině [1],[2] nebo také v angličtině [i], [ii]), případně na anglické Wikipedii. My se nyní radši podíváme na fyzikální aspekty speciální relativity.
3.1 Základní myšlenky STR
V naprosté většině učebnic můžeme najít takzvané postuláty speciální teorie relativity. To není nic neobvyklého. Všechny fyzikální teorie (a obecně teorie jakéhokoli druhu) musí vycházet z nějakých základních faktů nebo alespoň tvrzení, která bereme jako daná, a z nich odvozujeme další poznatky. Takovým východiskům říkáme postuláty. STR má dva. Pojďme si je nyní uvést tak, jak jsou uvedeny ve středoškolské učebnici [4] a krátce okomentovat. Možných formulací těchto postulátů je samozřejmě mnoho.
- Princip relativity - Ve všech inerciálních vztažných soustavách platí stejné fyzikální zákony.
- Princip konstantní rychlosti světla - Ve všech inerciálních vztažných soustavách má rychlost světla ve vakuu stejnou velikost, a to nezávisle na pohybu světelného zdroje. Rychlost světla v libovolné inerciální vztažné soustavě je ve všech směrech stejná.
První postulát nám velice připomíná již zmíněný Galileiho princip relativity, je zde ovšem jeden zásadní rozdíl. Galileiho princip mluví striktně jen o mechanických jevech, nic neříká o jiných částech fyziky jako je optika, elektřina, jaderné reakce apod. Až do příchodu STR nebyl princip relativity rozšířen na další jevy, protože k tomu nebyl jednoznačný důvod. Nemechanické jevy musely být nejdříve dostatečně prozkoumány (což je v případě elektromagnetismu a optiky převážně záležitost devatenáctého století). Motivací k zahrnutí i dalších jevů pod princip relativity byla snaha vyhovět novým experimentům a zároveň (nejen) Einsteinova víra v univerzálnost fyziky a tím pádem i zákonů, kterými ji popisujeme. Jestliže Galilei původně tvrdil, že uzavřeni v dopravním prostředku nedokážeme jakýmkoli mechanickým experimentem poznat, zda prostředek stojí nebo se pohybuje rovnoměrně přímočaře, Einstein tvrdí (či lépe řečeno předpokládá), že to nedokážeme poznat ani žádným jiným typem experimentu.
Druhý postulát, princip konstantní rychlosti světla, je přímým důsledkem experimentů provedených Michelsonem a spol. Namísto toho, aby se snažil tyto experimenty vyhodnotit v kontextu běžně uznávané fyziky, bere Einstein jejich podivný výsledek jako fakt (aniž by ho nějak vysvětlil) a ten zároveň používá jako odrazový můstek k fyzice nové. Navíc znamenal tento směr uvažování odklon od éteru jako fyzikální nutnosti. STR existenci éteru nijak nepředpokládá, ani nepotřebuje. Proto se dnes ve školách o žádném éteru nic nedozvíme. Byl opuštěn jako zbytečný koncept.
Poznámka 3.1
Dnešní pohled na věc říká, že elektromagnetické vlnění je šíření změn elektrického a magnetického pole. Tyto změny jsou provázány, takže se nikdy nevyskytují jen ty elektrické nebo ty magnetické. A obě tato pole mohou existovat i ve vakuu – dva magnety nebo dva elektricky nabité předměty na sebe budou působit, i když nejsou obklopeny například vzduchem. Proto se světlo může šířit, aniž by bylo vázáno na nějakou substanci.
Podívejme se, jaké důsledky z těchto postulátů plynou.
Relativistický vlak
Před tím, než dáme našim úvahám pevný matematický základ, ukážeme si na následujícím příkladu, jak překvapivé mohou být naše závěry, pokud se rozhodneme držet základních předpokladů STR. Tento myšlenkový pokus lze nalézt ve většině úvodních knih a textů o STR, nicméně považujeme ho za natolik důležitý, že ho stručně provedeme i zde.
Příklad 3.1:
Mějme libovolný dopravní prostředek (řekněme vlak), který se pohybuje rovnoměrně přímočaře rychlostí o velikosti v vůči zemi, kterou považujeme za inerciální soustavu. Proto i soustava souřadnic spojená s vlakem bude inerciální. Náš kolega ve vlaku vyšle světelný signál ze zdroje u podlahy kolmo vzhůru, nechá ho odrazit zase zpátky od zrcátka ve vzdálenosti \(L\) a bude měřit, za jak dlouho signál urazí dráhu tam a zpět. Naměří časový interval \(\Delta{}t^\prime\). Nyní může určit rychlost světelného signálu v čárkované soustavě vlaku jako \begin{equation*}\tag{3.1}\label{3.1} c^\prime=\frac{2L}{\Delta{}t^\prime} \end{equation*} Jaká je situace v soustavě země? Vlak se vůči zemi pohybuje zmíněnou rychlostí v a stejně tak se pohybuje zdroj světelného signálu a zrcátko. Dráha světelného signálu je v soustavě země jiná než v soustavě vlaku, protože je ovlivněna jejich vzájemným pohybem (jak vidíme níže na obrázku).
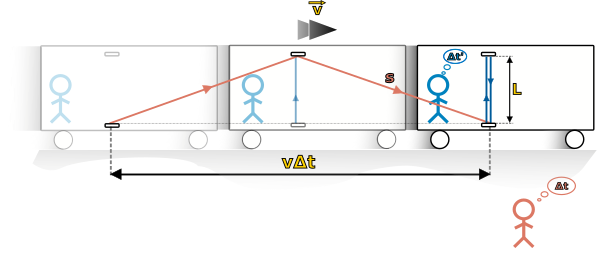
Obrázek 3.2 Průběh světelného signálu ve dvou různých inerciálních soustavách. V horní části obrázku vidíme jedoucí vlak ve třech okamžicích - vyslání světelného signálu, odraz signálu a jeho návrat. Modrá dráha (čárkovaná soustava) je pro přehlednost rozdělena na dvě, které by ale správně měly splývat.
Dráha signálu v nečárkované soustavě musí být větší než jen \(2L\). Základna velkého trojúhelníku je dráha, kterou vlak ujede po čas našeho měření, tedy \(v\Delta{}t\). Potom pro pravoúhlé trojúhelníky na obrázku podle Pythagorovy věty platí \begin{equation*}\tag{3.2}\label{3.2} s^2=L^2+\left(\frac{v\Delta{}t}{2}\right)^2 \end{equation*} a samozřejmě rychlost světelného signálu v nečárkované soustavě spojené se zemí vypočítáme jako \begin{equation*}\tag{3.3}\label{3.3} c=\frac{2s}{\Delta{}t}. \end{equation*} Pokud má platit druhý postulát o shodné rychlosti světla ve všech inerciálních soustavách, tedy \(c=c^\prime\), musí podle rovnic \eqref{3.1} a \eqref{3.3} zřejmě platit \begin{equation*} c=c^\prime => \frac{s}{\Delta{}t}=\frac{L}{\Delta{}t^\prime} . \end{equation*} Protože vzdálenosti \(s\) a \(L\) zjevně nejsou stejné, musí se lišit i časy \(\Delta{}t\) a \(\Delta{}t^\prime\). To ale znamená, že čas, za který proběhl daný fyzikální děj (cesta světelného signálu od jednoho zrcadla ke druhému a zpět), není v obou soustavách stejný. Jinými slovy, čas neplyne pro oba pozorovatele stejně. Dříve než se na tento překvapivý důsledek podíváme blíže, pojďme zkusit vyjádřit ještě vztah mezi naměřenými časovými intervaly. Vyjádříme si z rovnic \eqref{3.1} a \eqref{3.3} dráhy a v souladu s druhým postulátem již budeme v obou soustavách považovat rychlost světla za stejnou (dává smysl si ponechat nečárkované značení c): \begin{equation*} L=\frac{c\Delta{}t^\prime}{2},\qquad s=\frac{c\Delta{}t}{2}, \end{equation*} dosadíme do rovnice \eqref{3.2} a následně upravíme: \begin{align*} \left(\frac{c\Delta{}t}{2}\right)^2&=\left(\frac{c\Delta{}t^\prime}{2}\right)^2+\left(\frac{v\Delta{}t}{2}\right)^2/\cdot 4 \\[5pt] c^2(\Delta{}t)^2&=c^2(\Delta{}t^\prime)^2+v^2(\Delta{}t)^2 \\[5pt] (\Delta{}t)^2(c^2-v^2)&=c^2(\Delta{}t^\prime)^2 \\[5pt] (\Delta{}t)^2&=\frac{c^2(\Delta{}t^\prime)^2}{(c^2-v^2)}=\frac{\left(\Delta{}t^\prime\right)^2}{\left(1-\frac{v^2}{c^2}\right)} . \end{align*} Po odmocnění dostáváme \begin{align*}\tag{3.4}\label{3.4} &\Delta{}t=\Delta{}t^\prime \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}, \\ & \\ &\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\stackrel{def}{=}\gamma(v). \\ \end{align*} Lomený výraz s odmocninou se vyskytuje v STR tak často, že má své vlastní označení \(\gamma\) a bývá nazýván Lorentzův faktor nebo také gama faktor. V závorce zdůrazňujeme, že závisí čistě jen na relativní rychlosti dvou inerciálních soustav (když nepočítáme univerzální konstantu \(c\)). Všimněme si několika důležitých vlastností gama faktoru. Předně pro nadsvětelné rychlosti (v>c) by nám vycházela odmocnina ze záporného čísla. Při použití tohoto vzorce je tedy nutno se omezit na podsvětelné rychlosti (téma rychlosti světla jako limitní rychlosti pro fyzikální děje si necháme na později). Za druhé, pokud se omezíme na rychlosti menší než rychlost světla, gama faktor je vždy větší než jedna. Pro libovolnou podsvětelnou rychlost nám tím pádem vychází \(\Delta{}t>\Delta{}t^\prime\). Vidíme tedy, že stejný optický jev – cesta signálu k hornímu zrcátku a zpět - v různých vztažných soustavách trval rozdílnou dobu.
Z tohoto příkladu plyne jeden důležitý závěr pro naše další úvahy. Abychom vyhověli principu konstantnosti rychlosti světla, budeme zřejmě muset přehodnotit některé naše klasické představy týkající se času.
Prostor + čas = prostoročas
Dříve jsme poznali Galileiho transformaci, matematické vyjádření přechodu z jedné inerciální soustavy do druhé v řeči souřadnic. Z ní pak plynuly některé důležité závěry klasické mechaniky v čele s pravidlem o skládání rychlostí. To je ale v rozporu s principem konstantní rychlosti světla (také můžeme říci s invariancí rychlosti světla). Abychom vyhověli základním předpokladům STR, potřebujeme novou transformaci souřadnic, na jejímž základě vyvodíme nové důsledky.
Nejdříve si shrňme naši výchozí pozici. V mechanice se zabýváme pohybem těles, proto potřebujeme popsat prostor pomocí jeho tří souřadnic. Každý bod prostoru je tak pro nás v dané souřadné soustavě reprezentován trojicí čísel \((x,y,z)\). Nezajímá nás jen poloha předmětů, ale i jejich pohyb, to znamená změna polohy s časem. Čas je pro nás typicky parametr, tedy něco na čem všechny souřadnice obecně závisí, ale co se přímo neúčastní fyzikálních procesů. Tuto závislost většinou zdůrazňujeme zápisem \((x(t),y(t),z(t))\), což ale není nic jiného než vhodná zkratka za: V čase \(t=0\:\text{s}\) bylo těleso na souřadnicích \((x(0\:\text{s}),y(0\:\text{s}),z(0\:\text{s}))\), o sekundu později bylo v čase \(t=1\:\text{s}\) na souřadnicích \((x(1\:\text{s}),y(1\:\text{s}),z(1\:\text{s}))\) a tak dále. To důležité je, že v klasické mechanice automaticky předpokládáme, že tento čas plyne pro všechna tělesa a pozorovatele stejně. Jestliže pro nás uběhne 10 sekund, přijde nám samozřejmé, že pro cestující v okolo jedoucím autobuse také uběhlo 10 sekund. Tato představa je podpořena naším každodenním vnímáním, a proto ji v klasické mechanice samozřejmě používáme. Ale každý, kdo někdy viděl libovolnou optickou iluzi, ví, že naše vnímání nás může klamat.
Ve snaze vyhovět principu invariantní rychlosti světla jsme si rozmysleli, že klasický přístup k měření času nás velice snadno může dovést ke sporu. Budeme tedy nuceni ze svých předpokladů o čase slevit. Konkrétně musíme připustit, že pro různé inerciální soustavy může plynout čas různě. Pokud se máme s posádkou letící rakety shodnout na velikosti rychlosti světla, budeme se muset lišit v měření času. Prakticky řečeno, přidáme každé inerciální soustavě její vlastní parametr vyjadřující čas v dané soustavě.
Každá soustava tedy bude popisovat události pomocí svých souřadnic \((x,y,z)\) a k tomu také svého konkrétního času \(t\), který neplyne obecně stejně pro různé soustavy. Pracovat zvlášť s trojicí prostorových souřadnic a zvlášť s časem není příliš praktické. Ukazuje se proto být praktičtější používat namísto původní trojice souřadnic \((x,y,z)\) a času ubíhajícího někde v pozadí rovnou čtveřici \((t,x,y,z)\).
Poznámka 3.2
Stejně tak bychom mohli čas zařadit na konec závorky (nebo v podstatě kamkoli, je ale dobré si ve věcech udržet pořádek). My budeme čas umisťovat na začátek výčtu souřadnic a mluvit o něm a označovat ho jako nultou souřadnici. Tím že jsme časový parametr povýšili (nebo degradovali, podle toho jak se to vezme) na úroveň souřadnice, budeme moci například kompaktněji vyjádřit transformace mezi inerciálními soustavami a obecně se nám tak počítání a zápis rovnic trochu zjednodušší.
Toto formální propojení prostoru a času do jednoho celku nazýváme prostoročas a popisujeme ho pomocí třech prostorových souřadnic a jedné časové. Podobně jako u roviny říkáme, že je dvourozměrná (potřebujeme k jejímu popisu dvě souřadnice) a prostor je trojrozměrný (tři souřadnice), říkáme o prostoročase, že je čtyřrozměrný. Zatímco v obyčejném prostoru každá trojice čísel určuje jednoznačně bod, v prostoročase každá uspořádaná čtveřice čísel určuje konkrétní událost (vyjádřenou přesným místem a časem).
O událostech můžeme samozřejmě mluvit i v klasické mechanice. Pokud dvěma bouchnutím do stolu přiřknu polohy v souřadné soustavě a časy, kdy se odehrála, jistě je mohu nazvat událostmi. Z pohledu jiné soustavy budou mít tyto události obecně odlišné prostorové souřadnice (měříme vzdálenost od jiného místa), ale bude je dělit stejný čas (klasický přístup, podle kterého plyne čas pro všechny soustavy stejně). Naproti tomu ve speciální relativitě se může čas (vzpomeňte na rovnici \eqref{3.4}) mezi dvěma událostmi lišit pro různé inerciální soustavy.
3.2 Lorentzova transformace a její důsledky
Když už tedy víme, že Galileiho transformace, základ přecházení mezi inerciálními soustavami klasické fyziky, není v souladu s druhým postulátem speciální teorie relativity, pojďme nyní najít novou, speciálně relativistickou transformaci. Náš postup bude tak zpočátku téměř čistě matematický. Nejdříve odvodíme nové transformační vztahy a pak se podíváme, jaké fyzikální důsledky z nich plynou a ty pak podpoříme výsledky experimentů.
Mějme, stejně jako u Galileovy transformace, nečárkovanou inerciální soustavu souřadnic \(S\), která pro nás bude v klidu, a čárkovanou inerciální soustavu \(S^\prime\), jež se vůči té nečárkované pohybuje rychlostí \(v\). Do směru vzájemného pohybu soustav umístíme jak osu \(x\) tak osu \(x^\prime\) a i zbylé osy budou orientované shodně (vzpomeňte na obrázek 2.1). Dále budeme předpokládat následující:
- Žádná ze soustav není preferována. Z hlediska fyziky jsou rovnocenné a tuto vlastnost by měla respektovat i transformace souřadnic. (vizte I. postulát STR)
- V obou inerciálních soustavách naměří pozorovatelé stejnou hodnotu rychlosti světla ve vakuu. (vizte II. postulát STR)
- Dá se ukázat, že když se vzájemný pohyb odehrává pouze ve směru x-ových os, zůstanou souřadnice y a z nezměněny. Tento závěr v našem případě použijeme jako předpoklad. Poučeni příkladem se světelným signálem ve vlaku také připustíme, že se bude měnit časová souřadnice.
S využitím těchto základních předpokladů lze odvodit tzv. Lorentzovu transformaci: \begin{equation*}\label{Lor}\tag{3.5} t^\prime=\gamma\left(t-\frac{vx}{c^2}\right) \qquad x^\prime=\gamma\left(x-vt\right) \qquad y^\prime=y \qquad z^\prime=z. \end{equation*} Odvození není těžké, pouze trochu zdlouhavé. Zájemci si ho mohou rozbalit níže. Pojďme se nyní podívat na fyzikální důsledky této nové transformace.
Transformaci souřadnic mezi dvěma inerciálními pozorovateli, která by těmto podmínkám vyhovovala, budeme hledat ve tvaru \begin{equation*}\tag{3.5a}\label{3.5a} x^\prime=Ax+Bt \qquad \qquad t^\prime=Cx+Dt \end{equation*} Proč právě takto? Proč vystupují v rovnicích \eqref{3.5a} nečárkované souřadnice pouze v první mocnině namísto mocnin většího řádu nebo složitějších matematických funkcí? Důvodem je náš požadavek, aby popis v obou souřadných systémech odpovídal fyzikální realitě. Představme si například, že by se v jedné ze soustav nacházely tři předměty na třech od sebe stejně vzdálených místech (kupříkladu \(x_1=1,x_2=2\) a \(x_3=3\)). Ačkoli dovolujeme, aby jednotlivé vzdálenosti byly jinak veliké v druhé soustavě (to znamená, že pohybující se pozorovatel naměří odlišné délky), kdyby souřadnice \(x\) vystupovala v \eqref{3.5a} v jiné než první mocnině, vyšlo by nám, že v čárkované soustavě jsou tyto předměty různě daleko od sebe (např. pro \(x^\prime=Ax^2\) bychom měli \(x_1^\prime=A,x_2^\prime=4A\) a \(x_3^\prime=9A\)). Jelikož výsledek, že v jedné soustavě souřadnic jsou předměty pravidelně rozloženy a v jiné ne, se zdá být silně nefyzikální, dostáváme požadavek, aby se prostorové souřadnice transformovala lineárně (první mocniny). Stejný argument platí i pro časovou souřadnici a několik okamžiků pravidelně rozložených v čase. Lineární transformace také zaručuje, že pohyb objektů, na něž nepůsobí síly, je rovnoměrný a přímočarý v obou inerciálních soustavách.
Vycházíme tedy ze dvou rovnic \eqref{3.5a}. Nejprve se zaměříme na počátky jednotlivých systémů souřadnic. Pro čárkovaný počátek \(O^\prime\) z definice platí \(x^\prime=0\). Zároveň se pohybuje rychlostí v ve směru osy \(x\), takže z hlediska systému \(S\) pro jeho nečárkovanou prostorovou souřadnici platí \(x=vt\). Když tyto podmínky dosadíme do transformace, dostáváme \begin{equation*} x^\prime=Avt+Bt=0⇒ B=-Av. \end{equation*} Podobnou úvahu můžeme aplikovat i pro nečárkovaný počátek. Pro něj samozřejmě platí \(x=0\) a z pohledu čárkované soustavy se pohybuje rychlostí \(–v\) (mínus, protože v opačném směru). V čárkovaných souřadnicích pro něj tedy platí \(x^\prime=-vt^\prime\). Opět dosadíme do první transformační rovnice a zároveň použijeme i druhou pro \(t^\prime\): \begin{align*} x^\prime&=-Avt \\ -vt^\prime&=-Avt \\ -v(C\cdot0+Dt)&=-Avt \\ -v(Dt)&=-Avt⇒ A=D. \end{align*}
Počet neznámých konstant se nám tedy snížil na dvě, A a C. Transformační rovnice v tuto chvíli vypadají takto \begin{equation*} x^\prime=A(x-vt) \qquad \qquad t^\prime=Cx+At. \end{equation*}
Princip relativity nám dále říká, že na celou situaci můžeme stejně platně nahlížet i obráceně. Z pohledu čárkované soustavy se ta nečárkovaná pohybuje rychlostí \((-v)\) (jak už bylo použito výše). Transformace ale musí nabývat stejný tvar. Z této úvahy vyvodíme, že pro nečárkovanou souřadnici musí platit \(x=A(x^\prime+vt^\prime)\).
Dále použijeme základní postulát, podle kterého je rychlost světla \(c\) v obou soustavách stejná. Vyšleme-li paprsek z nečárkovaného počátku v kladném směru osy \(x\) v okamžiku, kdy se počátky míjejí, bude se pro pozorovatele v nečárkovaném systému šířit podle rovnice \(x=ct\). Podle druhého postulátu ho pozorovatel v čárkovaném systému popíše podobně rovnicí \(x^\prime\) musí splňovat \(x^\prime=ct^\prime\). Pomocí těchto podmínek dosadíme za časové souřadnice \(t\) a \(t^\prime\) do rovnic pro souřadnice \(x\) a \(x^\prime\): \begin{align*} x^\prime&=A\left(x-vt\right)=A\left(x-v\frac{x}{c}\right)=Ax\left(1-\frac{v}{c}\right) \\ x&=A\left(x^\prime+vt^\prime\right)=A\left(x^\prime+v\frac{x^\prime}{c}\right)=Ax^\prime\left(1+\frac{v}{c}\right). \end{align*} Tyto dvě rovnice vynásobíme mezi sebou: \begin{align*} xx^\prime&=A^2xx^\prime \left(1-\frac{v}{c}\right)\left(1+\frac{v}{c}\right) \\ 1&=A^2 \left(1-\left(\frac{v}{c}\right)^2\right) \\ A&=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} . \end{align*}
Konstanta \(A\) se ve STR vyskytuje velmi často. Natolik, že má své vlastní jméno. Říká se jí Lorentzův faktor a značí se malé řecké \(\gamma\) (gama). Odtud také plyne často používané označení gama-faktor. I my ji budeme nadále značit \(\gamma\).
Zbývá nám určit ještě konstantu \(C\). Tu dostaneme jednoduše dosazením podmínek pro světelný signál v obou soustavách \(x=ct\) a \(x^\prime=ct^\prime\) do první transformační rovnice \eqref{3.5a}, kam dosadíme za \(x\), \(x^\prime\) i \(t\): \begin{align*} x^\prime&=\gamma\left(x-vt\right) \\ ct^\prime&=\gamma\left(ct-v\frac{x}{c}\right) /:c \\ t^\prime&=\gamma\left(t-\frac{v}{c^2}x\right) \end{align*} Tím dostáváme rovnou transformační rovnici pro čárkovanou časovou souřadnici, kde vidíme, že na místě konstanty \(C\) se objevil člen \(-\gamma v⁄c^2\). Dostali jsme tak kompletní podobu Lorentzovy transformace, která je v souladu s postuláty STR, jako \begin{equation*} t^\prime=\gamma\left(t-\frac{vx}{c^2}\right) \qquad x^\prime=\gamma(x-vt) \qquad y^\prime=y \qquad z^\prime=z. \end{equation*}
Připomeňme, že \(\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\) , kde \(v\) je vzájemná rychlost dvou inerciálních soustav a \(c\) rychlost světla ve vakuu.
Tyto čtyři rovnice v transformaci \eqref{Lor} nám říkají, jak od souřadnic v inerciálním systému, který je vůči nám v klidu, přejít k souřadnicím pozorovatele, který se vůči nám pohybuje rovnoměrně přímočaře. Co když budeme chtít postupovat obráceně? K tomu potřebujeme inverzní (opačnou) transformaci, kterou můžeme najít dvěma způsoby. Buďto se na rovnice pro \(t^\prime\) a \(x^\prime\) budeme dívat jako na soustavu, ze které vyjádříme dvě neznámé \(t\) a \(x\), nebo využijeme principu relativity. Podle něj je stejně jako náš pohled platný i pohled pozorovatele z čárkované soustavy, který je vůči své soustavě v klidu, a my se pohybujeme vzhledem k němu rychlostí \((–v)\). Mínus proto, že z pohledu soustavy \(S^\prime\) se pohybujeme na opačnou stranu než soustava \(S^\prime\) vůči nám (tento postup jsme už mimochodem potkali v předchozí části). Takže transformace z čárkované soustavy do té naší musí mít stejný tvar jako \eqref{Lor}, jen s opačným znaménkem u rychlosti. Čtenář si může sám ověřit, že oba způsoby dopadnou stejně: \begin{equation*}\label{invLor}\tag{3.6} t=\gamma\left(t^\prime+\frac{vx^\prime}{c^2}\right) \qquad x=\gamma\left(x^\prime+vt\right) \qquad y=y^\prime \qquad z=z^\prime. \end{equation*}
Díky tomu, že Lorentzova transformace je lineární stejně jako ta Galileiho, i zde můžeme stejné vztahy použít rovnou také pro rozdíly souřadnic. Ilustrujeme si to na příkladu rozdílu časové souřadnice \(\Delta{}t^\prime\), který definujeme jednoduše jako \(\Delta{}t^\prime=t_2^\prime-t_1^\prime\). Pro první i druhou souřadnici platí transformace \eqref{Lor}, takže \begin{equation*} \Delta{}t^\prime=t_2^\prime-t_1^\prime=\gamma\left(t_2-\frac{vx_2}{c^2}\right)-\gamma\left(t_1-\frac{vx_1}{c^2}\right)=\gamma\left(t_2-t_1\right)-\gamma\frac{v}{c^2}\left(x_2-x_1\right) =\gamma\Delta{}t-\gamma\frac{v}{c^2}\Delta{}x=\gamma\left(\Delta{}t-\frac{v\Delta{}x}{c^2}\right). \end{equation*} Podobný výsledek dostaneme i pro druhou transformační rovnici. Vidíme tedy, že totožné rovnice můžeme používat rovnou pro rozdíly souřadnic, celkem \begin{equation*}\label{3.7}\tag{3.7} \Delta{}t^\prime=\gamma\left(\Delta{}t-\frac{v\Delta{}x}{c^2}\right) \qquad \Delta{}x^\prime=\gamma\left(\Delta{}x-v\Delta{}t\right) \qquad \Delta{}y^\prime=\Delta{}y \qquad \Delta{}z^\prime=\Delta{}z \end{equation*} a obdobně pro zpětnou transformaci \begin{equation*}\label{3.8}\tag{3.8} \Delta{}t=\gamma\left(\Delta{}t^\prime+\frac{v\Delta{}x^\prime}{c^2}\right) \qquad \Delta{}x=\gamma\left(\Delta{}x^\prime+v\Delta{}t^\prime\right) \qquad \Delta{}y=\Delta{}y^\prime \qquad \Delta{}z=\Delta{}z^\prime. \end{equation*} Než přistoupíme ke konkrétním příkladům, všimněme si, že odvozená transformace (stejně jako u odvození v příkladu relativistického vlaku) obsahuje výraz \(1/\sqrt{1-v^2/c^2}\) a proto funguje pouze pro \(v\lt{}c\), tedy tzv. podsvětelné rychlosti (pro rychlost větší než \(c\) dostáváme odmocninu ze záporného výrazu a pro \(v=c\) dělíme ve zlomku nulou). To ještě není důkaz, že by se nic nemohlo pohybovat rychleji než světlo, minimálně to ale znamená, že naši teorii lze aplikovat pouze pro situace, kdy se dvě inerciální soustavy vůči sobě pohybují podsvětelnou rychlostí. Proto se v dalším budeme zabývat pouze těmito situacemi. K problematice rychlosti světla jako nejvyšší možné rychlosti ve vesmíru se vrátíme v kapitole Nadsvětelné rychlosti.
Dilatace času
Představme si nyní raketu (abychom si na chvilku odpočinuli od vlaků a autobusů), která kolem Země prolétá konstantní rychlostí například \(v=0{,}8\:c\), tj. \(80\:\%\) rychlosti světla, směrem k Marsu (je třeba také poznamenat, že aby byla soustava rakety opravdu inerciální, musí svými motory vykompenzovat gravitační působení planet i Slunce). Do směru jejího letu opět umístíme osu \(x\) naší souřadné soustavy a i \(x^\prime\) soustavy spojené s raketou, aby se nám dobře počítalo (souřadnice \(y\) a \(z\) tak budou opět beze změny a v dalším je budeme pro přehlednost vynechávat). Umíme měřit vzdálenosti v prostoru kolem sebe a umíme odměřovat čas na našich hodinkách (vzpomeňte na ideální měřící tyče a ideální hodiny z první kapitoly). Stejně tak lidé v raketě mají své měřící tyče a hodiny, takže i oni jsou schopni měřit.
Každá událost \(U\) je v naší nečárkované soustavě popsána svými souřadnicemi \(U[t,x]\), tedy námi změřeným časem a polohou. Může jí být tiknutí hodinek, úder zvonu, srážka dvou aut, prakticky cokoli, co se stane v jeden konkrétní čas na jednom konkrétním místě. Stejnou událost mohou ale zpozorovat i naši kolegové z rakety (přiřadíme jim čárkovanou soustavu), obecně ale naměří jiný čas a jinou polohu \(U[t^\prime,x^\prime]\). Abychom byli konkrétní, zvolme si například za první událost průlet rakety kolem Země. Druhou událostí bude průlet rakety kolem Marsu. Vzdálenost od Země k Marsu se samozřejmě neustále mění kvůli obíhání planet kolem Slunce, vezměme tedy pro snadnější výpočet například jejich nejmenší vzdálenost, tj. \(54{,}6\cdot10^9\:\text{m}\), což je tím pádem zároveň prostorový rozdíl \(\Delta{}x\) mezi dvěma událostmi v naší soustavě spojené se Zemí. Z logiky věci pak plyne, že prostorová souřadnice první události v této soustavě je \(x_\text{U1}=0\:\text{m}\) a druhé události \(x_\text{U2}=54{,}6\cdot10^9\:\text{m}\).
Snadno spočítáme, jak dlouho raketa letí k Marsu v naší soustavě spojené se Zemí. Jedná se o jednoduchý rovnoměrně přímočarý pohyb, takže pro dobu letu musí platit \begin{equation*} \Delta{}t=\frac{\Delta{}x}{v}=\frac{54{,}6\cdot10^9\:\text{m}}{0{,}8\cdot3\cdot10^8\:\text{m}\cdot\text{s}^{-1}}=227{,}5\:\text{s}=3\:\text{min}\:47{,}5\:\text{s}. \end{equation*} V řeči souřadnic, pokud v soustavě Země přiřadíme první události čas \(t_{U1}=0\:\text{s}\), čas druhé události musí být \(t_{U2}=227{,}5\:\text{s}\). Jak dlouhý čas uplyne během letu k Marsu na vesmírné lodi? Abychom dokázali na tuto otázku odpovědět, stačí využít transformační rovnice pro časový interval \(\Delta{}t^\prime\). S využitím \(\Delta{}x=v\Delta{}t\) a definice gama faktoru dostáváme \begin{equation*}\label{3.9}\tag{3.9} \Delta{}t^\prime=\gamma\left(\Delta{}t-\frac{v\Delta{}x}{c^2}\right)=\frac{\Delta{}t-\frac{v\Delta{}x}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{\Delta{}t-\frac{v^2\Delta{}t}{c^2} }{\sqrt{1-\frac{v^2}{c^2}}}=\frac{\Delta{}t\left(1-\frac{v^2}{c^2}\right)}{\sqrt{1-\frac{v^2}{c^2}}}=\Delta{}t\sqrt{1-\frac{v^2}{c^2}}. \end{equation*}
Náš výsledek je obecně platný a rovnou vidíme, že pro posádku na lodi mezi oběma událostmi uplyne méně času, protože pro podsvětelné rychlosti pohybu bude odmocnina na pravé straně menší než jedna. Konkrétně pro námi zvolené hodnoty vychází \begin{equation*} \Delta{}t^\prime=227{,}5\cdot\sqrt{1-\frac{(0,8c)^2}{c^2}}\:\text{s}=227{,}5\cdot\sqrt{1-0{,}64}\:\text{s}=227{,}5\cdot0{,}6\:\text{s}=136{,}5\:\text{s}=2\:\text{min}\:16{,}5\:\text{s}. \end{equation*} To znamená, že čas, který uplyne pro posádku rakety je \(0{,}6\) krát menší. Jinak řečeno, pokud si zvolíme jak na Zemi, tak na lodi v okamžiku průletu kolem Země čas \(t_{U1}=t^\prime_{U1}=0\:\text{s}\) (tj. začneme se synchronizovanými hodinami v obou soustavách), při příletu lodi k Marsu budou hodiny na Zemi ukazovat \(227{,}5\:\text{s}\) a na lodi \(136{,}5\:\text{s}\).
Obecný závěr rovnice \eqref{3.9} tedy je, že v pohybující se inerciální soustavě plyne čas pomaleji než v naší klidové soustavě (jak ale uvidíme za chvilku, úplně stejnou věc může tvrdit i posádka rakety o Zemi). Tomuto jevu se říká dilatace času a je dán čistě vzájemným pohybem našich dvou inerciálních soustav. Samozřejmě posádka na lodi žádné zpomalení nepozoruje, protože vztah \eqref{3.9} se netýká jen např. zpomalení hodin, ale všech fyzikálních procesů včetně těch biologických. Nemůžeme pozorovat zpomalení času, pokud se zpomalíme sami. Jediné, čeho si posádka lodi všimne, je že k planetě Mars se podle vlastního času dostane \(0{,}6\) krát dříve než činí klasická předpověď. K této neshodě se ještě vrátíme. Dilatace času totiž není jediný zajímavý důsledek Lorentzovy transformace.
Kontrakce délek
Ukažme nyní, že ani na délce cesty se posádka lodi s námi na Zemi neshodne. Koneckonců, jeden ze základních postulátů STR je nezávislost rychlosti světla ve vakuu na inerciální soustavě. Jelikož rychlost (měřená v metrech za sekundu) závisí na měření času a délky, a již víme, že na měření času se obě soustavy neshodnou, nemohou se shodnout ani na měření vzdáleností. Dosaďme informace známé z nečárkované soustavy \(\Delta{}x\) a \(\Delta{}t\) do transformační rovnice pro polohu: \begin{equation*}\label{3.10}\tag{3.10} \Delta{}x^\prime=\frac{\Delta{}x-v\Delta{}t}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{54{,}6\cdot10^9-0{,}8\cdot3\cdot10^8\cdot227{,}5}{0{,}6}\:\text{m}=0\:\text{m}. \end{equation*}
Na první pohled se zdá zvláštní, že nám vychází nula. Není přece možné, aby posádka rakety naměřila mezi oběma planetami nulovou vzdálenost, když jim cesta trvá z jejich pohledu přes dvě minuty. Po bližším pohledu ale vlastně není tento výsledek překvapivý, protože v čitateli je výraz \(\Delta{}x-v\Delta{}t\), ale jelikož víme, že v soustavě Země je \(\Delta x\) rovna dráze uražené lodi, tj. \(\Delta{}x=v\Delta{}t\), zlomek musel nutně vyjít nula. Zamysleme se nad tím, co jsme vlastně vypočítali. Představte si, že byste jeli autem z Prahy do Ostravy. Když jste v Praze, vaše vzdálenost od Prahy je nulová. Když pak dorazíte do Ostravy, vaše vzdálenost od Ostravy je samozřejmě také nulová. No a nula mínus nula je nula. V našem případě s lodí je to přesně takové. Výraz \(\Delta{}x^\prime\) definován jako rozdíl délkových souřadnic obou planet v čárkované soustavě, tedy měřeno vzhledem ke kosmické lodi. V okamžiku průletu kolem Země je raketa v blízkosti Země, tedy délková souřadnice první události je nula (zajisté se najde někdo ze čtenářů, který si řekne, že to není možné, vždyť by loď musela proletět středem Země. Detailisty můžeme uklidnit tím, že loď samozřejmě prolétá kolem Země, je od ní tak sice v okamžiku průletu nějak vzdálena, ale naše souřadná soustava je nastavena tak, aby tato vzdálenost byla čistě ve směru např. y, nemá tedy na naší fyzikální situaci vliv). U druhé události, příletu k Marsu, je to obdobné. Vzdálenost lodi od Marsu je také nula. Budeme to tedy muset zkusit jinak.
Co to vlastně znamená změřit délku něčeho? Máme-li například určit délku nějaké tyče, která je vůči nám v klidu, není to nic obtížného. Prostě určíme polohu obou konců a hledaná délka je vzdálenost mezi nimi. Komplikovanější je, co když se vůči nám tyč pohybuje. V tom případě už si nemůže dát načas a nejdříve změřit polohu jednoho konce a pak druhého, protože tyč se mezitím o nějaký kus pohne a naše měření nebude určitě správné. Z toho plyne, že potřebujeme určit polohu obou konců najednou, tj. současně. Abychom tedy zjistili, jak velkou vzdálenost \(\Delta x^\prime\) mezi planetami posádka rakety naměří, vezmeme si jako dvě události - změření polohy jedné a druhé planety posádkou (ponechme nyní stranou technickou stránku věci). Jelikož musí být události současné, platí pro ně \(\Delta t^\prime=0\). Potřebujeme tedy rovnici, ve které se bude vyskytovat jak \(\Delta t^\prime\), tak \(\Delta x^\prime\). Nabízí se využít opačnou transformaci pro vzdálenost \eqref{3.8}:
\begin{equation*} \Delta{}x=\gamma(\Delta{}x^\prime+v\Delta{}t^\prime)=\gamma\Delta{}x^\prime=\frac{\Delta{}x^\prime}{\sqrt{1-\frac{v^2}{c^2}}}⇒\Delta{}x^\prime=\Delta{}x\sqrt{1-\frac{v^2}{c^2}}. \end{equation*}Dosazením konkrétních hodnot dostáváme \(\Delta{}x^\prime=54{,}6\cdot10^9\cdot0{,}6\:\text{m}=32{,}76\cdot10^9\:\text{m}\). Posádka v raketě tedy naměří vzdálenost mezi planetami \(0{,}6\) krát menší, stejně jako tomu bylo u času letu. Tomuto jevu říkáme kontrakce délek. Není náhodou, že nám míra dilatace času a kontrakce délek vyšly stejně. Muselo to tak nutně být právě díky jednomu ze dvou základních kamenů celé teorie – principu relativity.
Princip relativity v praxi
Použijme rovnou náš poslední výsledek pro vypočítání rychlosti lodi z pohledu posádky samotné. Ta z definice musí být vzdálenost mezi planetami vydělená dobou letu(vizte obrázek 3.3 níže), obojí samozřejmě v čárkované soustavě: \begin{equation*} v^\prime=\frac{\Delta{}x^\prime}{\Delta{}t^\prime}=\frac{\Delta{}x\sqrt{1-\frac{v^2}{c^2}}}{\Delta{}t\sqrt{1-\frac{v^2}{c^2}}}=\frac{\Delta{}x}{\Delta{}t}=v. \end{equation*} Náš výsledek je zcela v souladu s principem relativity, podle kterého jsou si všechny inerciální soustavy fyzikálně rovny. Proto jsme také dosud mluvili o vzájemné (nebo relativní) rychlosti dvou těles. Koneckonců, bylo by opravdu zvláštní, kdyby se Země z pohledu rakety vzdalovala jinak rychle než raketa od Země.
Princip relativity nám ale říká i další důležitou věc. Pokud se nyní vžijeme do role posádky na lodi, je to Země, která se vzdaluje rychlostí \(v\) na opačnou stranu a my na lodi jsme z našeho pohledu v klidu. Všechny úvahy o dilataci času a kontrakci délek musí platit i v tomto případě a to zcela symetricky. Už jsme si ukázali, že když stojíme na Zemi, vychází nám, že na lodi uplyne během letu méně času. Pokud ale stojíme na lodi, vyjde nám totožným postupem jako před tím, že je to Země, kde uplyne méně času. Jak je toto možné? Kdo má tedy pravdu?
Odpovědí je, že pravdu mají obě soustavy. Jeden z aspektů klasické mechaniky, který musíme ve speciální relativitě opustit je pojem absolutního času neboli myšlenku, že existuje jedno obecně platné a univerzální plynutí času. Čas je relativní a jeho plynutí je otázka naší perspektivy. Je to velmi podobné, jako když se na sebe budeme koukat s kamarádem či kamarádkou na větší vzdálenost, např. \(500\:\text{m}\). Když si v tu chvíli zavoláme mobilem, kamarád nám radostně oznámí, že podle něj jsme zmenšení. Na to můžeme ale my odvětit, že to není žádná pravda, my jsme velcí normálně, je to kamarád, kdo je maličký. Kdo má tedy pravdu zde?
Téměř jistě odpovíte, že ani jeden, ale v tuto chvíli jde o to, co reálně naměříme. My skutečně vidíme kamaráda zmenšeného a on či ona vidí zmenšené nás. Pravdu máme tedy vlastně oba (anebo, přinejmenším, mluvíme pravdu). Rozdíl v našem vnímání (měření) je samozřejmě dán perspektivou, na kterou jsme dobře zvyklí z každodenního života, a nikdo netvrdí, že například budovy na obzoru jsou ve skutečnosti maličké. Na druhou stranu, pokud chceme změřit výšku těchto budov, musíme buďto k budovám dojít (zmenšit vzájemnou vzdálenost na nulu) nebo použít nějakou chytrou geometrii a výšku budov dopočítat (tj. přeložit náš první pohled na situaci jako bychom vedle budovy skutečně stáli).
Stejně tak, pokud bychom chtěli porovnat plynutí času na Zemi a vesmírné lodi, musí mezi sebou posádka a lidé na planetě nějak komunikovat. Například vyměňovat si elektromagnetické signály (se započítáním doby lety signálů). Alternativně můžeme mezi měřeními v obou soustavách přepočítávat pomocí „chytré“ (tedy pro nás Lorentzovy) transformace souřadnic.
Relativní není samozřejmě jen dilatace času. Podobně to dopadne i pro kontrakci délek. Již jsme odvodili, že posádka v lodi naměří vzdálenost mezi Zemí a Marsem kratší než na Zemi. To proto, že z pohledu posádky se Země i Mars pohybují. Platí samozřejmě i opačný efekt. Loď se vůči Zemi pohybuje, proto ji pozorovatelé na Zemi naměří zkrácenou ve směru pohybu a to ve stejném poměru jako posádka naměřila zmenšení vzdálenosti planet. Dokážeme to jednoduchým výpočtem, kdy do transformační rovnice (3.10) dosadíme \(\Delta{}t=0\:\text{s}\), opět proto, že změřit délku nějakého tělesa znamená změřit polohu obou konců současně (tentokrát ale v soustavě Země). Dostáváme \begin{equation*} \Delta{}x^\prime=\frac{\Delta{}x-v\Delta{}t}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{\Delta{}x}{\sqrt{1-\frac{v^2}{c^2}}}\implies\Delta{}x=\Delta{}x^\prime\sqrt{1-\frac{v^2}{c^2}}. \end{equation*} Pokud tedy například loď bude měřit na délku \(\Delta{}x^\prime=100\:\text{m}\) (měřeno v klidové soustavě lodi, mluvíme o tzv. klidové délce), naměří na Zemi délku \(\Delta{}x=100\cdot0,6\:\text{m}=60\:\text{m}\). Obecný závěr tedy zní: jakmile se něco vůči nám bude pohybovat, naměříme délku tohoto tělesa zkrácenou ve směru pohybu (protože souřadnice \(y\) a \(z\) zůstávají beze změny). Celý příklad nám shrnuje následující obrázek:

Obrázek 3.3 Cesta ze Země na Mars z pohledu inerciální soustavy Země (nahoře) a posádky rakety (dole).
Relativita v malých rychlostech
Velice správná otázka by v tuto chvíli byla, proč tyto podivné efekty běžně nepozorujeme. Denně jezdíme dopravními prostředky tam a zpátky, přesto nevidíme žádné zkracování délek ani se nám nerozcházejí hodinky s ostatními. Vysvětlení je vcelku prosté. Všední rychlosti, kterými se pohybujeme na Zemi, jsou příliš malé na to, aby se relativistické efekty dostatečně projevily. Matematicky tato skutečnost vyplývá přímo z Lorentzovy transformace \eqref{Lor}. Hlavním činitelem vystupujícím ve všech rovnicích je zmíněný gama faktor. Pro relativní rychlosti \(v\) menší než je rychlost světla bude výraz \(v/c\) vždy menší než jedna a stejně tak jeho druhá mocnina. Výraz pod odmocninou bude tedy kladný, což je dobře... protože je pod odmocninou. Můžeme si tedy povšimnout, že Lorentzova transformace nefunguje pro vzájemné rychlosti větší než \(c\) (ba dokonce rovné \(c\)). Více se o tomto faktu zmíníme v kapitole Nadsvětelné rychlosti. Prozatím se pojďme podívat, jak se chová gama faktor při rychlostech výrazně menších než rychlost světla, tedy prakticky ve všech situacích, které zažíváme na naší planetě.
V matematice se zavádí tzv. Taylorovy polynomy, což je způsob, jak přepsat obecně složité matematické výrazy jako nekonečnou řadu jednodušších sčítanců mocnin. Setkáváme se s nimi typicky poprvé až na vysoké škole, ale pro naše účely není nyní důležité, jak fungují. Taylorův polynom pro gama faktor začíná takto \begin{equation*} \gamma=\frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2 }}=1+\frac{1}{2}\left(\frac{v}{c}\right)^2+\frac{3}{8}\left(\frac{v}{c}\right)^4+... , \end{equation*} kde místo tří teček pokračují členy s vyššími mocninami členu \(v/c\). První člen na pravé straně je jednička, která by odpovídala nulové rychlosti, kdy k žádným kontrakcím délek ani dilataci času nedochází. Tím vlastně odpovídá i klasické fyzice, která dané efekty vůbec nepředpovídá. Protože se zabýváme situacemi, kdy je člen \(v/c\) menší než jedna, znamená to, že členy s vyššími mocninami dávají stále menší a menší příspěvky.
Vezměme si například automobil jedoucí po dálnici konstantní rychlostí \(120 \frac{\text{km}}{\text{hod}}\doteq33{,}3 \frac{\text{m}}{\text{s}}\). Pak je \( \frac{v}{c}\doteq1{,}1\cdot10^{-7}\), \((\frac{v}{c})^2 \doteq 1{,}2\cdot10^{-14}\) a \((\frac{v}{c})^4\doteq1{,}5\cdot10^{-28}\). Vidíme tedy, že gama faktor se v takovém případě liší od jedničky nejvíce v řádu \(10^{-14}\), to znamená v řádu stobiliontin (\(0{,}000 000 000 000 01\)). Pokud budeme chtít v tomto případě spočítat přesnou hodnotu gama faktoru, i ta nejlepší příruční kalkulačka nám dá výsledek \(1{,}0000000000000062\) a další desetinná místa již nezvládne. Proto pro malé rychlosti bohatě vystačíme jen s prvními dvěma členy na pravé straně. Ve výsledku pak není překvapivé, že relativistické efekty na Zemi příliš nepozorujeme, protože jak my lidé, tak většina běžně dostupných přístrojů není schopná zachytit rozdíly v tak malých řádech. Je to řádově stejná situace, jako kdyby vám někdo podal třiceticentimetrové pravítko a řekl, že je ve skutečnosti o jeden femtometr (\(10^{-15}\:\text{m}\) - což je mimochodem zhruba rozměr atomového jádra) kratší. Vám to může být s klidným svědomím jedno, protože se tato nepřesnost nijak prakticky neprojeví.
Ukažme si některé další příklady. V následující tabulce je uvedeno několik vybraných rychlostí, konkrétně rychlost francouzského rychlovlaku TGV, komerčního tryskového letounu typu Airbus, vysokorychlostního náboje .204 Ruger používaného v loveckých puškách a následně maximální dosažená rychlost sondy JUNO, která v tuto chvíli (léto 2019) obíhá planetu Jupiter a je považována za jeden z nejrychleji se pohybujících člověkem vyrobených objektů vůbec (uvedená rychlost je maximální dosažená vzhledem k Zemi a během letu sondy se samozřejmě mění).
| Tabulka 3.1 Gama faktory pro vybrané rychlosti | |||
|---|---|---|---|
| \(v / (\text{km}\cdot\text{h}^{-1})\) | \(v / (\text{m}\cdot\text{s}^{-1})\) | \(\gamma\) faktor* | |
| Rychlovlaky TGV | 300 | 83 | 1,0000000000000383 |
| Komerční tryskový letoun | 955 | 265 | 1,0000000000003907 |
| Náboj .204 Ruger | 4320 | 1200 | 1,0000000000080111 |
| Vesmírná sonda JUNO | 265000 | 73611 | 1,0000000301449142 |
Z tabulky vidíme, že v našich podmínkách nízkých rychlostí nemáme prakticky možnost reálně relativistické efekty pozorovat. Jakých rychlostí bychom tedy museli dosáhnout? Snadný výpočet nám ukazuje, že abychom dosáhli gama faktoru alespoň \(1{,}001\), museli bychom vyvinout rychlost mírně převyšující \(4{,}5\:\%\) rychlosti světla (cca \(1{,}34\cdot 10^7 \: \text{m}\cdot\text{s}^{-1}\)- tj. 13400 kilometrů za sekundu). Pro gama faktor rovný třem polovinám by byla potřeba rychlost přibližně \(75\:\%\:c\). Speciální teorii relativity je tedy třeba brát v potaz hlavně při relativně vysokých rychlostech vůči rychlosti světla. Záleží samozřejmě na přesnosti, kterou od svých výpočtů a měření vyžadujeme.
3.3 Důkazy ve prospěch STR
Relativistické miony
Jak už bylo řečeno, každá teorie musí být ověřena praxí. V průběhu dvacátého stolení bylo provedeno mnoho experimentálních testů, než si STR od svého vzniku získala mezi vědci své stoupence a stala se uznávanou fyzikální teorií. Ukažme si, jakým způsobem je možné ověřit existenci dilatace času jako reálného fyzikálního jevu. Nejpříhodnější k tomu jsou elementární částice. Důležitou vlastností každé částice je její poločas rozpadu. Čas, za jaký se nestabilní částice rozpadne, se obecně nedá předpovědět přesně. Ale i když nedokážeme říci, za jak dlouho se rozpadne každý jednotlivý radioaktivní atom nebo nestabilní elementární částice, dokážeme využít matematiku pravděpodobnosti a předpovídat něco pro větší množství částic.
Řekněme, že takových částic máme \(N\). Potom jejich poločas rozpadu je doba, po které jich zbude už jen polovina. Tak například pro radioaktivní izotop polonia \(_{84}^{210}\text{Po}\) je udáván poločas rozpadu přibližně 138 dní. To znamená, že pokud například začneme s jedním gramem tohoto izotopu, po uplynutí 138 dní ho zbude už jen půl gramu, zatímco zbytek se radioaktivně rozpadne na jiné prvky. Po dalších 138 dnech už bude jen čtvrt gramu (tedy polovina z poloviny) a tak dále. Vždy po uplynutí poločasu najdeme nerozpadlou polovinu původního množství atomů.
Stejný princip platí i pro elementární částice. Některé jsou velmi stabilní a jejich rozpad ještě nebyl pozorován (například protony) a některé se rozpadají na jiné částice ve zlomcích vteřiny po svém vzniku. Slavným příkladem jsou miony (částice podobné elektronu, ale mnohem těžší a méně stabilní). Miony mají podle laboratorních měření poločas rozpadu zhruba \(1{,}52\cdot10^{-6}\) s (miliontiny sekundy). Je známo, že hojně vznikají v naší atmosféře typicky ve výšce kolem \(15\:\text{km}\) nárazem kosmického záření do molekul vzduchu a posléze pronikají k povrchu planety rychlostí kolem \(0{,}99c\) (budeme počítat s touto hodnotou), kde je pak můžeme detekovat. Překvapivě je ale detekováno mnohem víc těchto částic, než by se dalo na základě nerelativistické fyziky očekávat. Speciální relativita podala na tento problém odpověď.
Miony urazí při své rychlosti vzdálenost \(15\:\text{km}\) za čas \(\Delta{}t=5{,}1\cdot10^{-5}\:\text{s}\) (všechny hodnoty uvádíme zaokrouhlené). To odpovídá více jak 33 poločasům rozpadu. Předpokládejme, že v atmosféře vznikne za jednu vteřinu N mionů. Pak bychom neměli na povrchu detekovat více než \(N⁄2^{33}\) částic. STR nám ale říká, že pro mion plyne čas pomaleji. Jeho rychlost \(0{,}99 c\) vůči nám odpovídá gama faktoru přibližně \(7{,}1\). V klidové soustavě mionu proto během patnáctikilometrové cesty uplyne čas pouze (prakticky se jedná jen o verzi vztahu \eqref{3.9} a stejně tak bychom mohli použít \(\Delta t^\prime=\Delta t/\gamma\)) \begin{equation*} \Delta{}t^\prime=\gamma\left(\Delta{}t-\frac{v\Delta{}x}{c^2}\right)=7{,}1\left(5{,}1\cdot10^{-5}-\frac{0{,}99\cdot15\cdot10^3}{3\cdot10^8 }\right)\:\text{s}\doteq7{,}13\cdot10^{-6}\:\text{s}, \end{equation*} čemuž odpovídá necelých pět poločasů rozpadu. To znamená, že ve skutečnosti se rozpadne jenom o něco málo méně než \(\frac{N}{2^5}=\frac{N}{32}\), což je mnohonásobně méně, než jsme odhadli bez použití STR.
Vlastně se zde opakuje myšlenka s posádkou lodi rozebíraná výše. Celá situace musí jít vysvětlit i z hlediska mionů samotných (v jejich klidové soustavě). Rychlost mionů vůči klidné Zemi je samozřejmě stejná jako rychlost Země v klidové soustavě těchto částic. Koneckonců, mluvíme o relativní vzájemné rychlosti. Z pohledu mionů tedy neurazí námi naměřenou délku \(15\:\text{km}\), ale díky kontrakci délek pouze \begin{equation*} \frac{15\:\text{km}}{\gamma}=15\:\text{km}\sqrt{1-\frac{v^2}{c^2}}=15\:\text{km}\sqrt{1-0{,}99^2}\doteq2{,}12\:\text{km}, \end{equation*} proto se jich tolik nestihne rozpadnout.
Podobný experiment byl skutečně proveden v roce 1941 pány Rossim a Hallem ve Spojených státech. Ti proměřovali rozdíly v počtech mionů s výškovým rozdílem 2 km a jejich výsledky dobře odpovídaly předpovědím speciální relativity. Experimenty stejného typu byly od té doby provedeny i s jinými částicemi a stále lépe potvrzují STR. Pro obsáhlý a podrobný rozbor mnoha experimentů ohledně speciální relativity v angličtině doporučujeme [iv].
Relativistické protony
Dobrým příkladem, kdy je již zcela nutné počítat v rámci STR a nikoli klasické mechaniky, je velký hadronový urychlovač (LHC – Large Hadron Collider) Evropské organizace pro jaderný výzkum (CERN). Z uváděných energií srážek protonů lze odvodit velikost gama faktoru těsně před srážkou zhruba kolem \(7200\), což odpovídá rychlosti přibližně \(99{,}999999\:\%\) rychlosti světla.
Celý projekt výstavby tohoto zařízení přišel na úctyhodných \(5{,}2\) mld. eur a spolupracovalo při něm několik tisíc vědců z celého světa, takže ho jen těžko někdo může brát na lehkou váhu. Přitom je v současné době asi největším důkazem, že speciální relativita správně popisuje reálné jevy při vysokých rychlostech. Pojďme se podívat, jakým způsobem vstupuje relativita do experimentů na urychlovači.
Předně si musíme říct, že dilatace času a kontrakce délek nejsou jediné nové jevy, které s sebou STR přináší. Velmi brzy po zveřejnění této své teorie Einstein ukázal, že aby zůstal v platnosti zákon zachování hybnosti, musíme klasický vztah pro hybnost \(\vec{p}=m\vec{v}\) libovolného tělesa či částice modifikovat. Pokud má těleso hmotnost \(m_0\), když je vzhledem k nám v klidu (mluvíme o tzv. klidové hmotnosti), bude jeho hybnost vůči nám při vzájemné rychlosti \(v\) \begin{equation*}\label{3.11}\tag{3.11} p=\gamma{}m_0v=\frac{m_0v}{\sqrt{1-\frac{v^2}{c^2}}}. \end{equation*}
Z předchozího rozboru chování gama faktoru je opět patrné, proč žádné změny v hybnosti oproti klasické mechanice nemůžeme při malých rychlostech pozorovat, ale při rychlostech blízkých \(c\) se už bude jistě jednat o nezanedbatelný přírůstek. Konkrétně u protonů srážených v LHC jsme uvedli velikost gama faktoru přibližně \(7200\), z čehož plyne, že protony se chovají v naší klidové soustavě, jako by měly \(7200\)krát větší hybnost (což si ne zcela správně, ale za to názorně, můžeme představit, jako kdyby byly \(7200\)krát těžší).
Na střední škole se učíme o síle působící na nabitou částici v magnetickém poli. Pokud částice vlétne do magnetického pole kolmo na indukční čáry, bude touto silou její trajektorie zakřivena do kružnice. Tímto způsobem se také zakřivuje dráha protonů v LHC. Ze známého poloměru \(r\) dráhy, po které mají protony obíhat, můžeme určit potřebnou velikost magnetické indukce pole \(B\). Protože se magnetická síla rovná síle dostředivé (to je ta, co zakřivuje dráhu částice), platí podle klasické mechaniky \begin{equation*} F_m=F_d \implies Bev=\frac{m_0v^2}{r} \implies B=\frac{m_0v}{re} \end{equation*} (\(e\) je zde elektrický náboj protonu, který je velikostně stejný jako elementární náboj elektronu, \(m\) je hmotnost protonu a \(v\) jeho rychlost). I z tohoto klasického odvození vidíme závislost velikosti magnetického pole na rychlosti protonu (to znamená, že magnetické pole je nutno zvětšovat s rostoucí rychlostí částic, aby se zakřivovaly po stále stejné dráze a nevyletěly z urychlovače). Pokud budeme brát v potaz speciální relativitu, dostaneme po trochu delším odvozování výraz opravený o gama faktor: \begin{equation*} B=\frac{\gamma{}m_0v}{re}=\frac{m_0v}{re\sqrt{1-\frac{v^2}{c^2}}}. \end{equation*} Jak jsme viděli u chování gama faktoru, pro vysoké rychlosti se tento výraz může už výrazně lišit od své klasické verze. Například podle výše uvedeného, aby protony při své rychlosti blízké \(c\) obíhaly v LHC stále po stejné kruhové dráze, musíme na ně podle STR působit více jak \(7000\)krát silnějším magnetickým polem než jak to říká klasické mechanika. Takže skutečnost, že urychlovače po celém světě fungují a používají relativistické vzorce namísto klasických, je velkým argumentem ve prospěch STR.
Poznámka 3.3
Teoretická poznámka: V mnoha knihách, zejména staršího data, můžeme najít zmínku o tzv. relativistické hmotnosti \(m(v)=\gamma(v)m_0\) (výjimečně zde zdůrazňujeme závislost gama faktoru na rychlosti). Výše zmíněný vztah pro hybnost k zavedení takového pojmu silně vybízí, protože pak nabývá klasického tvaru hybnost = hmotnost krát rychlost, pouze s tou změnou, že naměřená hmotnost tělesa, které se vůči nám pohybuje, je větší než klidová díky gama faktoru. Pojem relativistické hmotnosti může být ale matoucí a v některých novějších učebnicích je opouštěn. Rozhodně není v souladu s běžným chápáním hmotnosti jako množství hmoty. Tělesa s větší relativistickou hmotností není víc, nicméně se zdánlivě chová jako by bylo hmotnější než v klidu, to znamená, že je náročnější toto těleso urychlit nějakou silou. Zdálo by se logické tedy relativistickou hmotnost dát do souvislosti se setrvačnou hmotností ve smyslu, jak je zavedena ve 2. Newtonově zákonu \(\vec{F}=m\vec{a}\). Ukazuje se ale, že tato formulace není ve speciální relativitě platná. Z klasické mechaniky víme, že Newtonovu pohybovou rovnici můžeme alternativně zapsat pomocí změny hybnosti: \begin{equation*} \vec{F}=\frac{\Delta{}\vec{p}}{\Delta{}t}=\frac{\Delta(m\vec{v})}{\Delta{}t}=m\frac{\Delta{}v}{\Delta{}t}=m\vec{a} \end{equation*} a teprve díky předpokladu konstantnosti hmotnosti m ji můžeme ze změny hybnosti vyjmout, ze změny rychlosti za čas se stává zrychlení a máme klasickou verzi Newtonova zákona. Předpoklad konstantnosti hmotnosti (či lépe řečeno její nezávislosti na rychlosti tělesa) není v STR splněn, ať už používáme relativistickou hmotnost či ne, díky vztahu \eqref{3.11}. Z toho důvodu je v STR nutné obecně používat zmíněnou verzi pohybové rovnice se změnou hybnosti za čas, nikoli s hmotností a zrychlením. Dá se ukázat, že tento tvar pohybové rovnice v jednoduchém případě, kdy působící síla je ve směru pohybu tělesa, přejde na \begin{equation*} \vec{F}=\gamma^3m_0\vec{a} \end{equation*} (odvodit tento vztah není složité, ale striktně vzato k němu musíme umět derivace; zájemci si mohou odvození rozbalit níže). Poznamenejme ještě pro zajímavost, že v případě, kdy je působící síla kolmá na směr pohybu (jako je to právě v kruhovém urychlovači), přejde pohybová rovnice na tvar \(\vec{F}=\gamma m_0\vec{a}\).
Vidíme tedy, že nemůžeme zachránit původní tvar pohybové rovnice pouze přechodem od klidové hmotnosti k té relativistické, protože nám v pohybové rovnici vyskočilo gama na třetí, nikoli na prvou jak by to muselo být, kdybychom v Newtonově pohybovém zákonu čistě nahradili klidovou hmotnost za relativistickou. Proto ani my nadále nebudeme zavádět pojem relativistické hmotnosti, jak to můžete najít v jiných zdrojích. Toto propojení klasické mechaniky se speciální relativitou se může na první pohled zdát známé a nápomocné, ale může snadno vést k dezinterpretacím a mylným závěrům.
Pro správné odvození musíme vycházet z diferenciálního tvaru pohybové rovnice, které je platná i v STR, kam dosadíme hybnost podle rovnice \eqref{3.11}: \begin{equation*} \vec{F}=\frac{\text{d}\vec{p}}{\text{d}t}=\frac{\text{d}}{\text{d}t}\left(\frac{m_0\vec{v}}{\sqrt{1-\frac{v^2}{c^2}}}\right)=\frac{\text{d}}{\text{d}t}\left(m_0\gamma\vec{v}\right). \end{equation*} Protože situaci řešíme v jedné dimenzi (vektor síly je rovnoběžný se směrem rychlosti), ze všech vektorů se stanou skaláry (respektive používáme pouze složky vektorů v daném směru). Dále předpokládejme, že se klidová hmotnost \(m_0\) během pohybu nemění (například, že se nejedná o raketu, která by ze sebe chrlila hořící palivo a tím ztrácela hmotnost). V tom případě můžeme \(m_0\) vytknout před derivaci, protože nezávisí na čase. Podle pravidla pro derivaci součinu pak dostáváme \begin{equation*} F=m_0\left(\frac{\text{d}\gamma}{\text{d}t}v+\gamma\frac{\text{d}v}{\text{d}t}\right). \end{equation*} Vyřešme nejdříve první člen v závorce. Podle pravidla pro derivaci složené funkce platí \begin{equation*} \frac{\text{d}γ(v(t))}{\text{d}t}=\frac{\text{d}\gamma}{\text{d}v}\frac{\text{d}v}{\text{d}t}, \end{equation*} Spočítejme si zvlášť první z derivací: \begin{equation*} \frac{\text{d}\gamma}{\text{d}v}=\frac{\text{d}}{\text{d}v}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{-\frac{1}{2}\left(-\frac{2v}{c^2}\right)}{\left(1-\frac{v^2}{c^2}\right)^{\frac{3}{2}}} =\frac{\frac{v}{c^2}}{\left(1-\frac{v^2}{c^2}\right)^{\frac{3}{2}}} =\gamma^3\frac{v}{c^2}. \end{equation*} Po dosazení do našeho původního výpočtu a využití definice, že časová derivace rychlosti je zrychlení: \begin{equation*} F=m_0\left(\frac{\text{d}\gamma}{\text{d}v}\frac{\text{d}v}{\text{d}t}v+\gamma\frac{\text{d}v}{\text{d}t}\right)=m_0\left(\gamma^3 \frac{v}{c^2}av+\gamma{}a\right)=m_0\gamma\left(\gamma^2\frac{v^2}{c^2}+1\right)a. \end{equation*} Na závěr stačí už jen upravit výraz v závorce: \begin{equation*} \gamma^2\frac{v^2}{c^2}+1=\frac{\frac{v^2}{c^2}}{1-\frac{v^2}{c^2}}+\frac{1-\frac{v^2}{c^2}}{1-\frac{v^2}{c^2}} =\frac{\frac{v^2}{c^2}+\left(1-\frac{v^2}{c^2}\right)}{1-\frac{v^2}{c^2}}=\frac{1}{1-\frac{v^2}{c^2}}=\gamma^2. \end{equation*} Celkem tedy dostáváme \begin{equation*} F=m_0\gamma^3a. \end{equation*}
3.4 Pythagorova věta v prostoročase?!
Ukázali jsme si, že měření času a prostoru se může pro různé inerciální soustavy lišit. Navíc jsme odvodili Lorentzovu transformaci, která je převodníkem mezi prostoročasovými souřadnicemi jednoho a druhého inerciálního pozorovatele. Pojďme nyní ukázat, že existuje něco, na čem se mohou oba pozorovatelé shodnout. Nějaký můstek, který nám usnadní přechod a orientaci mezi navzájem se pohybujícími inerciálními soustavami.
Zkusme se inspirovat klasickou fyzikou, která popisuje svět jako trojrozměrný eukleidovský prostor. To je ten, o kterém se učíme na základní a střední škole. Součet úhlů v trojúhelníku má v tomto prostoru přesně \(180\:°\), dvě rovnoběžné přímky se nikdy prakticky neprotnou a tak dále. Můžeme tu zavést kartézskou soustavu, která má tři osy (pro každý rozměr jednu) a na ní souřadnice. V první části jsme si uvedli, že ať použijeme jakoukoli kartézskou soustavu souřadnic, bez ohledu na posunutí či rotaci, vzdálenost mezi dvěma konkrétními body, řekněme \(P\) a \(Q\), bude vždy stejná a platí \begin{equation*}\label{3.12}\tag{3.12} |PQ|^2=(x_Q-x_P)^2+(y_Q-y_P)^2+(z_Q-z_P)^2=(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2. \end{equation*} Nyní jsme v situaci, kdy místo s body o třech prostorových souřadnicích pracujeme s událostmi a čtyřmi souřadnicemi - jednou časovou a třemi prostorovými. Zkusme nyní, zda nebude mezi libovolnými dvěma událostmi platit analogie k Pythagorově větě. Definujme si nyní prostoročasovou „vzdálenost“ mezi dvěma událostmi \(U(t_1,x_1,y_1,z_1)\) a \(V(t_2,x_2,y_2,z_2)\) podle vzoru výrazu \eqref{3.12} jako \begin{equation*}\label{3.13}\tag{3.13} |UV|^2=K(\Delta{}t)^2+(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2. \end{equation*}
U rozdílu časových souřadnic předpokládáme výskyt nějaké konstanty \(K\), minimálně proto, že čas a vzdálenost mají jiné fyzikální jednotky a nechceme sčítat „jablka s hruškami“ (případně si můžete zkusit následující výpočet provést bez této konstanty a sami uvidíte, že vám nic rozumného nevyjde, to je taky celkem silný argument). Naše úvaha bude vcelku podobná té v první části textu týkající se invariance vzdálenosti vůči transformaci souřadnic. Události \(U\) a \(V\) mají samozřejmě své souřadnice i v čárkované soustavě, která se, jak už jsme si zvykli, pohybuje vůči nečárkované soustavě rovnoměrně přímočaře rychlostí \(v\). Aby byla prostoročasová „vzdálenost“ událostí stejná v libovolné inerciální soustavě, musí při použití Lorentzovy transformace (LT) platit
\begin{equation*}\tag{3.14}\label{3.14}
K(\Delta{}t)^2+(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2=K(\Delta{}t^\prime)^2+(\Delta{}x^\prime)^2+(\Delta{}y^\prime)^2+(\Delta{}z^\prime)^2.
\end{equation*}
Splnění této rovnice je náš požadavek. Prostým dosazením LT bychom tak mohli dostat podmínku určující konstantu \(K\). Výpočet není nijak náročný, jen trochu zdlouhavý. Rozkliknout si ho můžete níže. Plyne z něj jednoznačný závěr. Rovnice \eqref{3.14} bude splněna, pouze pokud bude platit \(K=-c^2,\) což je skvělý výsledek hned z několika důvodů. Jednak \(K\) není žádný složitý výraz na několik řádků, za což je člověk vždy vděčný, navíc v něm figuruje pouze rychlost světla jako univerzální konstanta (pomineme-li znaménko a druhou mocninu). A za další, vynásobení rychlostí na druhou dá výrazu \((\Delta{}t)^2\), původně v sekundách na druhou, stejnou jednotku jako mají ostatní členy, tedy metr na druhou. Sčítáme tedy jablka s jablky, jak to má být.
K tomuto závěru jsme došli pro libovolné dvě události, takže se můžeme oprostit i od jejich označení a zavedeme takzvaný prostoročasový interval (nazývaný také čtyřinterval) \(\Delta{}s\) - respektive jeho druhou mocninu:
\begin{equation*}\label{4int}\tag{3.15}
(\Delta{}s)^2=-c^2(\Delta{}t)^2+(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2.
\end{equation*}
Nyní odvodíme konstantu \(K\) vystupující v prostoročasovém intervalu \eqref{4int} na základě podmínky \eqref{3.14}, kterou požadujeme, aby se dva pozorovatelé v různých inerciálních soustavách shodli na velikosti tohoto intervalu. Jelikož víme, že popisy těchto dvou pozorovatelů jsou navzájem spojeny Lorentzovou transformací \eqref{Lor}, případně \eqref{3.7}, je to vlastně to samé jako požadovat, aby se výraz \eqref{3.13} při LT nezměnil. Jinými slovy, aby byl vůči ní invariantní. Protože souřadnice \(y\) a \(z\) se při naší zjednodušené transformaci rovnají v obou soustavách, bude platit \(\Delta y=\Delta y^\prime\) a \(\Delta z=\Delta z^\prime\) a z výpočtu je rovnou vynecháme. Členů ve vzorci budeme mít i tak dost.
Začneme intervalem mezi nějakými dvěma událostmi \((t_1^\prime,x_1^\prime,y_1^\prime,z_1^\prime)\) a \((t_2^\prime,x_2^\prime,y_2^\prime,z_2^\prime )\) v čárkované soustavě. Po vynechání \(y\)-ových a \(z\)-ových souřadnic vypadá takto: \begin{equation*}\label{3.16}\tag{3.16} (\Delta{}s^\prime)^2= K(\Delta{}t^\prime)^2+(\Delta{}x^\prime)^2. \end{equation*} Nyní použijeme Lorentzovu transformaci pro rozdíly souřadnic \eqref{3.7} \begin{equation*} \Delta{}x^\prime=\gamma(\Delta{}x-v\Delta{}t) \qquad \Delta{}t^\prime=\gamma\left(\Delta{}t-\frac{v\Delta{}x}{c^2}\right). \end{equation*} Po dosazení dostáváme \begin{equation*} (\Delta{}s^\prime)^2=K\gamma^2\left[(\Delta{}t)^2-\frac{2v\Delta{}x\Delta{}t}{c^2} +\frac{v^2(\Delta{}x)^2}{c^4} \right]+\gamma^2\left[(\Delta{}x)^2-2v\Delta{}x\Delta{}t+v^2(\Delta{}t)^2\right]. \end{equation*} Dáme k sobě členy se stejnými přírůstky souřadnic a vytkneme. \begin{align*} (\Delta{}s^\prime)^2&=(\Delta{}t)^2\left[K\gamma^2+v^2\gamma^2\right]+(\Delta{}x)^2\left[\frac{K\gamma^2v^2}{c^4}+\gamma^2\right]-\Delta{}x\Delta{}t\left[\frac{2K\gamma^2 v}{c^2}+2v\gamma^2\right] \\ &=(\Delta s)^2=K(\Delta t)^2+(\Delta x)^2 \\ \end{align*} Druhý řádek je náš požadavek, aby se oba čtyřintervaly rovnaly. To nastane jedině tehdy, když se budou rovnat koeficienty u jednotlivých přírůstků souřadnic (tj. například koeficient u \(\Delta t\) na jedné straně se musí rovnat koeficientu u \(\Delta t\) na té druhé). Musí být tedy splněny tři podmínky: \begin{align*} K\gamma^2+v^2\gamma^2=K \implies K=\frac{v^2\gamma^2}{1-\gamma^2} \\ \frac{K\gamma^2v^2}{c^4}+\gamma^2=1\implies K=\frac{(1-\gamma^2)c^4}{\gamma^2v^2} \\ \frac{2vK\gamma^2}{c^2}+2v\gamma^2=0\implies K=-c^2 \end{align*} Vypadá to jako tři různé rovnice, ale když dosadíme do první a druhé podmínky definici gama faktoru \(\gamma=1/\sqrt{1-v^2/c^2}\), zjistíme, že vedou ke stejnému výsledku jako ta třetí. To znamená, že interval \(\Delta{}s\) bude vůči Lorentzově transformaci invariantní, pokud bude \(K=-c^2\) a interval tak bude tvaru \begin{equation*} (\Delta{}s)^2=-c^2(\Delta{}t)^2+(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2. \end{equation*}
Takto definovaný výraz je tedy vůči LT invariantní (neměnný). To znamená, že pokud v jakékoli inerciální soustavě změříme časový rozdíl mezi dvěma událostmi a rozdíly v jejich prostorových souřadnicích a zkombinujeme je podle rovnice \eqref{4int} , dostaneme vždy stejné číslo. Nehledě na to, jak rozdílné je naše měření oproti jinému inerciálnímu pozorovateli vlivem naší vzájemné rychlosti, na hodnotě prostoročasového intervalu mezi dvěma danými událostmi se vždy shodneme.
Poznámka 3.4:
Všimněme si rozdílného znaménka mezi časovou a prostorovými souřadnicemi. Matematicky je tím vyjádřeno, že ač spojujeme čas a prostor do jednoho celku, je mezi těmito dvěma „typy“ souřadnic rozdíl. Prostoročas není to samé jako čtyřrozměrný prostor. Pro hypotetický čtyřrozměrný prostor bychom snadno odvodili čtyřrozměrnou Pythagorovu větu podobně, jako jsme odvodili tu třírozměrnou (ostatně na matematice je krásné, že teoreticky můžeme Pythagorovu větu definovat v libovolně dimenzionálním prostoru – a jsou matematické obory, kde se to opravdu využívá). Mírně zjednodušeně řečeno, libovolně rozměrný prostor, kde můžeme zavést patřičně rozměrnou verzi klasické Pythagorovy věty, nazýváme eukleidovský. Prostoročas, ve kterém se ve speciální relativitě pohybujeme, eukleidovský není kvůli rozdílným znaménkům v \eqref{4int}. Má ale také svůj název, nazývá se Minkowskiho prostoročas na německého matematika Hermanna Minkowskiho (1864 - 1909). Detailněji se geometrii prostoročasu budeme věnovat v části o obecné relativitě.
Poznámka 3.5:
Dodejme, že jsme v odvozování čtyřintervalu mohli postupovat i jinak a konstantu K umístit před všechny prostorové souřadnice. Dostali bychom podobný výsledek (pouze s \(-1/c^2\) ) a čtyřinterval bychom měřili najednou v sekundách místo v metrech. I tento způsob by byl v pořádku, ale zdá se zbytečně komplikované mít tři konstanty místo jedné. Protože je pro naši definici invariantu důležitý rozdíl ve znaménkách u časové a prostorových souřadnic, naše celá úvaha by fungovala, i kdybychom výraz v definici \eqref{4int} vynásobili mínus jedničkou. Prostoročasový invariant bychom pak definovali jako \begin{equation*} (\Delta{}s)^2=c^2(\Delta{}t)^2-(\Delta{}x)^2-(\Delta{}y)^2-(\Delta{}z)^2, \end{equation*} což je alternativní způsob, který se používá například v částicové fyzice, protože vede k hezčím (nikoli pravdivějším či správnějším) vztahům s hybností částice. Toto zavedení je pouze věcí konvence podobně, jako se kdysi zvolilo, že kladný směr otáčení je proti směru hodinových ručiček, a na fyzikální podstatě našich rovnic nic nemění.
Protože \(c\) je konstanta, můžeme ji vnořit do rozdílu souřadnic: \(c^2(\Delta{}t)^2=(\Delta{}ct)^2\). To znamená, že se na časový člen se záporným znaménkem můžeme dívat jako na změnu souřadnice \(ct\). Vyjádření souřadnice události jako \((ct,x,y,z)\) namísto \((t,x,y,z)\) je oblíbené, protože všechny souřadnice pak mají stejnou jednotku metr. Konzistentně s tímto přístupem můžeme vynásobit rovnici pro časovou souřadnici v LT rychlostí světla a dostat \begin{equation*} ct^\prime=\gamma\left(ct-\frac{vx}{c}\right). \end{equation*} Používání souřadnice \(ct\) místo \(t\) může vést k hezčím rovnicím a velmi praktické je při kreslení prostoročasových diagramů, kterým se ale v tuto chvíli věnovat nebudeme. Nicméně, fyzikálně se používáním souřadnice \(ct\) nic nemění, a my proto budeme pro větší názornost dále používat jen čistě časovou souřadnici.
Jak už bylo řečeno, fyzikálně důležitý je rozdíl ve znaménkách ve \eqref{4int}. Plyne z něj několik důležitých závěrů:
Za prvé, kvadrát prostoročasového intervalu může nabývat kladné, nulové i záporné hodnoty. Představme si, že sledujeme částici pohybující se konstantní rychlostí \(v\) od jedné události k druhé (což je stručné vyjádření toho, že částice je přítomna oběma událostem, je tedy ve správný čas na správném místě pro jednu i druhou událost). Označme námi změřenou prostorou vzdálenost, kterou částice uletí mezi událostmi jako \(l\). Platí tedy \(l^2=(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2\), a zároveň \(l=v\Delta t\), kde \(\Delta t\) je čas mezi oběma událostmi.
\((\Delta s)^2=0\)
Začněme mezním případem, kdy se interval mezi uvažovanými událostmi rovná nule. Pak plyne z \eqref{4int} \begin{equation*} c^2(\Delta{}t)^2=(\Delta{}x)^2+(\Delta{}y)^2+(\Delta{}z)^2=l^2 \implies c^2=\frac{l^2}{(\Delta{}t)^2} =v^2 \implies |v|=c. \end{equation*} Nulovost čtyřintervalu mezi dvěma událostmi tedy znamená, že pokud by měla být částice (či jakékoli jiné těleso) přítomna oběma událostem, musela by se mezi nimi pohybovat rychlostí světla. Samozřejmě se může jednat o šíření světla samotného (které si můžeme představit jako šíření fotonů) nebo jakékoli jiné částice, která se podle předpokladu dokáže pohybovat rychlostí světla (podle STR musí mít ale taková částice nulovou klidovou hmotnost a více se o tom zmíníme v podkapitole Nadsvětelné rychlosti). Nulovému čtyřintervalu se proto říká světlupodobný (light-like), někdy také světelný nebo prostě nulový.
Vraťme se nyní k našemu původnímu příkladu s lodí, která cestuje mezi Zemí a Marsem. Společně s průletem lodi kolem Země (událost \(U_1\) a připomeňme, že jsme zvolili \(t(U_1)=0\:\text{s}\)) vyšleme světelný signál k Marsu. Ten, pohybuje se rychlostí světla, dorazí k Marsu (událost \(U_3\)) samozřejmě dříve než kosmická loď (událost \(U_2\)), konkrétně za čas \(t(U_3)=\Delta{}x/c=54{,}6\cdot10^9\:\text{m}/3\cdot10^8\:\text{m}\cdot\text{s}^{-1} =182\:\text{s}\) (mimochodem, pokud se zavedených událostech začnete ztrácet, můžete využít jejich přehled v tabulce 3.2 níže). Jelikož \(U_1\) a \(U_3\) jsou spojeny světelným signálem, musí prostoročasový interval mezi nimi být nulový (což jsme si odvodili již obecně výše, ovšem můžete si sami dosadit správné rozdíly souřadnic a přesvědčit se). Tato hodnota bude stejná ve všech inerciálních soustavách, tedy i v čárkované soustavě kosmické lodi. Místo abychom si nejdříve spočítali čas, za který podle posádky lodi doletí světelný signál ze Země na Mars, a dosadili do výrazu pro čtyřinterval, zkusme to pro zajímavost udělat obráceně. Ukažme, že z nulovosti čtyřintervalu v čárkované soustavě plyne přirozený výpočet pro čas letu světelného signálu z hlediska čárkované soustavy. Nejprve si spočítáme vzdálenost mezi událostmi \(U_1\) a \(U_3\) podle posádky rakety pomocí Lorentzovy transformace \eqref{3.7} \begin{equation*} \Delta x^\prime=\frac{\Delta x-v\Delta t}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{54{,}6\cdot10^9-0{,}8\cdot3\cdot10^8\cdot182}{\sqrt{1-0{,}8^2}} \:\text{m}=18{,}2\cdot10^{9}\:\text{m}. \end{equation*} Prostoročasový interval mezi událostmi \(U_1\) a \(U_3\) musí být nulový, z čehož dostáváme přímo vzorec pro výpočet doby letu světelného signálu podle posádky rakety jako \begin{equation*} 0=-c^2(\Delta{}t^\prime)^2+(\Delta{}x^\prime)^2⇒c^2(\Delta{}t^\prime)^2 =(\Delta{}x^\prime)^2⇒\Delta{}t^\prime=\frac{\Delta{}x^\prime}{c}=\frac{18{,}2\cdot10^{9}\:\text{m}}{3\cdot10^8\:\text{m}\cdot\text{s}^{-1}}\doteq 60{,}7\:\text{s}, \end{equation*} což je, jak si můžete sami ověřit, přesně výsledek, který bychom dostali přímým použitím Lorentzovy transformace stejně jako u prostorové souřadnice.
\((\Delta s)^2\gt 0\)
Všimněme si teď případu, kdy bude kvadrát intervalu mezi dvěma událostmi kladný. Z jeho definice pak opět plyne podmínka pro rychlost částice přítomné oběma událostem: \begin{equation*} 0\lt-c^2(Δt)^2+l^2\implies{}c^2\lt{}\frac{l^2}{(Δt)^2}=v^2\implies{}|v|\gt{}c. \end{equation*} Naše rychlost by tedy musela být větší než rychlost světla. Protože máme dobré důvody se domnívat, že se nic hmotného nemůže touto rychlostí pohybovat (více v kapitole Nadsvětelné rychlosti), nepokládáme za možné, aby se mohly dvě události navzájem spojené kladným čtyřintervalem jakýmkoli způsobem ovlivnit. Stejně tak není možné, aby byl jeden pozorovatel přítomen oběma událostem. V tomto případě mluvíme o prostorupodobném (space-like) čtyřintervalu mezi událostmi. To proto, že vždy existuje nějaký inerciální systém, ve kterém jsou dané dvě události současné, a dělí je pouze prostorová vzdálenost.
Pojďme si pro názornost zavést událost \(U_4\) (začíná jich být hodně, ale nebojte, tahle je poslední), která se odehraje na Marsu například v čase \(t(U_4 )=60\:\text{s}\) z pohledu Země (takže \(\Delta t\) mezi \(U_1\) a \(U_4\) je \(60\:\text{s}\)). Snadno nahlédneme, že kvadrát čtyřintervalu mezi těmito dvěma událostmi je kladný: \begin{equation*} (Δs)^2=-(3\cdot10^8\:\text{m})^2(60\:\text{s})^2+(54{,}6\cdot10^9\text{m})^2\doteq 2{,}66\cdot10^{21}\:\text{m}^2>0\:\text{m}^2. \end{equation*} Ukažme, že existuje inerciální systém (označme ho jako dvoučárkovaný), ve kterém budou obě dvě události současné (jinými slovy existuje nějaká podsvětelná rychlost \(v^{\prime\prime}\) kterou bychom se museli pohybovat, abychom obě události naměřili jako současné). Stačí využít transformační rovnice pro rozdíl časových souřadnic \begin{equation*} Δt^{\prime\prime}= \gamma\left(Δt-\frac{v^{\prime\prime}Δx}{c^2}\right)=0⇒Δt=\frac{v^{\prime\prime}Δx}{c^2}\quad \implies\quad v^{\prime\prime}=\frac{c^2Δt}{Δx}=\frac{3\cdot10^8\cdot60}{54{,}6\cdot10^9}c\doteq 0{,}33\:c , \end{equation*} kde jsme využili faktu, že gama faktor se nemůže rovnat nule.
Podle našeho výsledku, pokud kolem Země poletí nějaký pozorovatel rychlostí přibližně třetiny rychlosti světla, naměří události \(U_1\) a \(U_4\) současně, jinými slovy vzdálené pouze v prostoru, nikoli v čase. Ještě zajímavější je ale časový interval mezi těmito dvěma událostmi z pohledu posádky naší původní rakety, tedy v čárkované soustavě. Ta letí rychlostí \(0{,}8\:c\), takže dostáváme \begin{equation*} Δt^\prime=\gamma\left(Δt-\frac{vΔx}{c^2}\right)=1{,}66\left(60-\frac{0{,}8\cdot54{,}6\cdot10^9}{3\cdot10^8}\right)\:\text{s}\doteq -142{,}7\:\text{s}. \end{equation*} Záporný výsledek se může zdát překvapivý, ale dává docela jasný smysl. Uvědomme si, co jsme právě spočítali. Sice jsme to pro stručnost neuváděli, ale všechny souřadnicové rozdíly jsou typu vzdálenější/pozdější – bližší/dřívější (bráno z pohledu Země, samozřejmě), matematicky zapsáno \(Δt=t_{U_4}-t_{U_1}\) a \(Δx=x_{U_4}-x_{U_1}\). Jestliže nám tedy vypočítaný rozdíl časových souřadnic událostí v čárkované soustavě \(Δt^\prime=t_{U_4}^\prime-t_{U_1}^\prime\) vychází záporný, znamená to, že pro posádku lodi se událost \(U_4\) na Marsu stane dříve než \(U_1\) na Zemi. Pravděpodobně se vám zdá zvláštní, že by se pořadí událostí mohlo pro různé pozorovatele lišit, ale to je přesně vlastnost událostí, které dělí prostorupodobný interval. Takové události se nemohou navzájem nijak ovlivnit (říkáme, že nejsou kauzálně propojeny), protože tento vliv by se musel šířit rychleji než světlo ve vakuu. Na pořadí, v jakém různí pozorovatelé tyto dvě události zaznamenají, tedy objektivně nezáleží, a proto relativita jejich pořadí (ač se nám může zdát zvláštní) ničemu neodporuje.
\((\Delta s)^2\lt 0\)
Nakonec jsme si nechali pro nás fyzikálně nejpodstatnější případ. Převládá-li ve výpočtu kvadrátu čtyřintervalu člen s rozdílem časových souřadnic, vyjde nám záporné číslo. Analogicky s předchozím to nastane tehdy, když je možné mezi danými dvěma událostmi cestovat podsvětelnou rychlostí: \begin{equation*} 0\gt-c^2(Δt)^2+l^2\implies{}c^2\gt{}\frac{l^2}{(Δt)^2}=v^2 \implies|v|\lt{}c. \end{equation*} Čtyřintervalu, který tuto podmínku splňuje, se celkem nepřekvapivě říká časupodobný (time-like). Například všechny události našeho života jsou spojeny časupodobnými čtyřintervaly, protože se mezi nimi pohybujeme rychlostí nižší než \(c\). Jistě si teď kladete otázku, jak může být druhá mocnina něčeho záporná? To zavání komplexními čísly! Ale nebojte, tak hrozné to nebude. Čtyřinterval sám o sobě totiž nemá přímý fyzikální význam. Pojďme si nyní ilustrovat, jak může záporný kvadrátu čtyřintervalu dát smysluplný fyzikální výsledek.
Vzpomeňme si na události \(U_1\) a \(U_2\), průlet první rakety kolem Země a následně kolem Marsu. Už víme, že kvadrát čtyřintervalu mezi těmito událostmi je invariantní vůči Lorentzově transformaci, jinými slovy, pokud ho spočítáme ve dvou různých soustavách, musíme dostat stejné číslo. V případě nečárkované soustavy (Země) a té čárkované (raketa pohybující se rychlostí \(0,8\:c\) vůči Zemi) dostáváme \begin{equation*} -c^2(\Delta{}t)^2+(\Delta{}x)^2=(\Delta{}s)^2=(\Delta{}s^\prime)^2=-c^2(\Delta{}t^\prime)^2+(\Delta{}x^\prime)^2. \end{equation*} Vzdálenost mezi událostmi \(U_1\) a \(U_2\) z pohledu čárkované soustavy \(\Delta{}x^\prime\) je nulová, protože je raketa přítomna oběma událostem (tento argument jsme rozebírali výše), a tak můžeme předchozí rovnici upravit jako \begin{equation*} -c^2(\Delta{}t^\prime)^2=(\Delta{}s^\prime)^2=(\Delta{}s)^2\implies(\Delta{}t^\prime)^2=-\frac{(\Delta{}s)^2}{c^2}\implies\Delta{}t^\prime=\frac{\sqrt{-(\Delta{}s)^2}}{c}\gt0. \end{equation*} Máme-li tedy dvě časupodobné události, určuje jejich čtyřinterval čas uplynulý mezi událostmi pro inerciálního pozorovatele přítomného u obou z nich. Mluvíme o tzv. vlastním času pozorovatele (to je ten, který odměřují hodinky cestující na jeho zápěstí). A protože čtyřinterval je i pro všechny ostatní inerciální pozorovatele stejný, všichni se na tomto vlastním času shodnou, či lépe řečeno, všichni si ho dokáží dopočítat. Znaménko mínus v odmocnině má také důležitý význam, protože díky němu je pod odmocninou kladné číslo a vše matematicky funguje.
Poznámka 3.6:
V poznámce 3.5 jsme se zmínili o opačné konvenci zavedení čtyřintervalu s kladným znaménkem u času a záporným u prostorových souřadnic. V této konvenci by nám znaménka kvadrátů čtyřintervalu vyšla obráceně. Časupodobný interval by tedy vycházel kladně, což může pro fyzikálně nejdůležitější případ vypadat jako logická volba. Je to také jedna z výhod této konvence, ale jak jsme viděli, není to nutné. Fyzikálně relevantní veličiny vycházejí stejně kladně. A hlavně, kdo si má pořád pamatovat tři mínusy :-)
Abychom ukázali všechny důležité teoretické aspekty, zavedli jsme 3 různé inerciální soustavy a čtyři události. Pojďme si je na konec této části shrnout a podívat se, v čem se liší a co mají společné:
| Tabulka 3.2 Shrnutí zavedených inerciálních soustav a událostí | ||
|---|---|---|
| značka | popis | |
| Vztažné soustavy | \(S\) | Soustava spojená se Zemí. |
| \(S^\prime\) | Raketa pohybující se rychlostí \(0{,}8\:c\) vůči Zemi. | |
| \(S^{\prime\prime}\) | Raketa pohybující se rychlostí přibližně \(0{,}33\:c\) vůči Zemi. | |
| Události | \(U_1\) | Průlet první rakety kolem Země a vyslání světelného signálu. |
| \(U_2\) | Průlet první rakety kolem Marsu. | |
| \(U_3\) | Světelný signál vyslaný při \(U_1\) dorazí k Marsu. | |
| \(U_4\) | Libovolná událost, která se odehraje na Marsu v čase \(60\:\text{s}\) po \(U_1\) z pohledu Země. | |
| Tabulka 3.3 Časové a prostorové rozdíly a kvadráty čtyřintervalu mezi událostmi | ||||
|---|---|---|---|---|
| Události | Vztažná soustava | \((\Delta{}t,\Delta{}t^\prime,\Delta{}t^{\prime\prime})/\text{s}\) | \((\Delta{}x,\Delta{}x^\prime,\Delta{}x^{\prime\prime})/\text{m}\) | \((\Delta{}s)^2/\text{m}^2\) |
| \(U_1 \rightarrow U_2\) | \(S\) | \(227{,}5\) | \(54{,}6\cdot10^9\) | \(-1{,}68\cdot10^{21}\) |
| \(S^\prime\) | \(136{,}5\) | \(0^*\) | \(-1{,}68\cdot10^{21}\) | |
| \(S^{\prime\prime}\) | \(177{,}4\) | \(34{,}0\cdot10^9\) | \(-1{,}68\cdot10^{21}\) | |
| \(U_1 \rightarrow U_3\) | \(S\) | \(182\) | \(54{,}6\cdot10^9\) | \(0\) |
| \(S^\prime\) | \(60{,}7\) | \(18{,}2\cdot10^9\) | \(0\) | |
| \(S^{\prime\prime}\) | \(129{,}2\) | \(38{,}8\cdot10^9\) | \(0\) | |
| \(U_1 \rightarrow U_4\) | \(S\) | \(60\) | \(54{,}6\cdot10^9\) | \(2{,}66\cdot10^{21}\) |
| \(S^\prime\) | \(-142{,}7^{**}\) | \(6{,}7\cdot10^{10}\) | \(2{,}66\cdot10^{21}\) | |
| \(S^{\prime\prime}\) | \(0^{***}\) | \(5{,}15\cdot10^{10}\) | \(2{,}66\cdot10^{21}\) | |
3.5 Relativistické skládání rychlostí
Vzpomeňme si nyní na klasický způsob skládání rychlostí. Ten je příjemně přímočarý. Pokud například kovboj pojede na koni rychlostí \(10\:\text{m}/\text{s}\) vůči zemi a vystřelí kulku ze své „henryovky“, u níž je udávána typická rychlost náboje těsně po výstřelu jako \(335\:\text{m}/\text{s}\) ve směru jízdy, bude se podle klasické fyziky náboj pohybovat rychlostí \(345\:\text{m}/\text{s}\) vůči zemi. Rychlosti shodného směru sčítáme, opačného směru odčítáme. Již jsme si ale ukázali, že tento postup by u světla nefungoval. Kdyby kovboj místo výstřelu z pušky posvítil z lucerny, bude se světlo z ní pohybovat rychlostí \(c\) všemi směry nejen vůči kovbojovi, ale i vůči zemi. Tento nesoulad mezi chováním světla a hmotných předmětů stál u zrodu STR a nyní bychom si měli ukázat, jak byl touto teorií vyřešen. Ukazuje se, že běžné sčítání rychlostí, ač pro malé rychlosti oproti rychlosti světla celkem přesné, není tak docela správné.
Mějme dvě inerciální souřadné soustavy. Čárkovaná soustava \(S^\prime\) (kovboj na koni) se pohybuje vůči nečárkované \(S\) (země) rychlostí \(V\) ve směru osy \(x\). V čárkované soustavě se určitý předmět (střela) pohybuje konstantní rychlostí \(v^\prime\) (tj. rychlost výstřelu vzhledem k pušce) ve směru osy \(x^\prime\). Chceme vědět, jakou rychlostí se bude pohybovat vůči nečárkované soustavě, označme ji \(v\). V nečárkované soustavě bude platit \(v=\Delta{}x⁄\Delta{}t\). Nyní stačí do této rovnice dosadit změny čárkovaných souřadnic pomocí inverzní LT \eqref{invLor} (je to samozřejmě stejný postup jako u klasického odvození, pouze s novou transformací souřadnic): \begin{equation*} v=\frac{\Delta{}x}{\Delta{}t}=\frac{\gamma(\Delta{}x^\prime+V\Delta{}t^\prime)}{\gamma(\Delta{}t^\prime+\frac{V\Delta{}x^\prime}{c^2})}=\frac{\Delta{}t^\prime(\frac{\Delta{}x^\prime}{\Delta{}t^\prime}+V)}{\Delta{}t^\prime(1+\frac{V}{c^2} \frac{\Delta{}x^\prime}{\Delta{}t^\prime})}=\frac{\frac{\Delta{}x^\prime}{\Delta{}t^\prime}+V}{1+\frac{V}{c^2}\frac{\Delta{}x^\prime}{\Delta{}t^\prime}}. \end{equation*} Protože v čárkovaných souřadnicích platí \(v^\prime=\Delta{}x^\prime/\Delta{}t^\prime\), získali jsme tak relativistický vzorec pro skládání rychlostí: \begin{equation*}\label{sklRych}\tag{3.16} v=\frac{v^\prime+V}{1+\frac{Vv^\prime}{c^2}}. \end{equation*}
Jak dopadne situace s kovbojem a lucernou? V takovém případě bude \(v^\prime=c\) a z našeho pohledu se bude světlo pohybovat rychlostí \begin{equation*} v=\frac{c+V}{1+\frac{cV}{c^2}}=\frac{c+V}{1+\frac{V}{c}}=\frac{c+V}{\frac{1}{c}\left(c+V\right)}=c\frac{c+V}{c+V}=c , \end{equation*} což je přesně výsledek, který souhlasí s reálným chováním světla. Zároveň si můžeme ukázat, že pomocí tohoto skládání rychlostí nikdy nepřekročíme rychlost světla. Dejme tomu, že se kosmická sonda bude pohybovat vůči zemi rychlostí \(0{,}8c\). Sonda změří ve směru svého pohybu rychlost nějaké částice na \(0{,}5c\). Jakou rychlost částice naměříme ze Země? \begin{equation*} V=\frac{0{,}5c+0{,}8c}{1+\frac{0{,}5\cdot0{,}8c^2}{c^2}}=\frac{1{,}3c}{1+0{,}4}\doteq0,93c \end{equation*} Nejenom, že rychlost částice vůči Zemi není očekávaných \(1{,}3 c\), ale je dokonce menší než rychlost světla samotná. „Pouze“ asi \(93\:\%\). Obecně sloučením dvou libovolných podsvětelných rychlostí dostaneme vždy opět podsvětelnou rychlost. Jak jsme také viděli, když se něco vůči jedné inerciální soustavě pohybuje rychlostí světla (třeba světlo z lucerny výše), dostaneme ze vztahu pro skládání rychlostí v jakékoli jiné inerciální soustavě opět rychlost světla. Musíme se ale vyvarovat nefyzikálním výrazům typu \(\Delta x/\Delta t^\prime\). Rychlost dává smysl jen jako změna polohy za změnu času obojí měřené v jedné vztažné soustavě.
Abychom získali vzorec pro přechod od rychlosti \(v\) k \(v^\prime\), můžeme buď vyjádřit \(v^\prime\) z rovnice \eqref{sklRych} nebo opět využijeme principu relativity, který nám říká, že situace při pohledu z čárkované situace musí vypadat zcela stejně, pouze nečárkovaná soustava se pohybuje rychlostí \(-V\). Takže \begin{equation*}\tag{3.17}\label{invRych} v^\prime=\frac{v-V}{1-\frac{Vv}{c^2}}. \end{equation*} Vidíme, že tyto relativistické vzorce mají „klasickou verzi“ skládání rychlostí v čitateli. Nově se nám objevil jmenovatel. Abychom si přiblížili chování skládání pro „malé“ rychlosti, dosaďme si do vztahu \eqref{3.16} zmíněné rychlosti kovboje na koni a výstřelu z pušky: \begin{equation*}\tag{3.18}\label{3.18} v=\frac{v^\prime+V}{1+\frac{Vv^\prime}{c^2}}=\frac{335+10}{1+\frac{10\cdot335}{(3\cdot 10^8)^2}}\:\text{m}\cdot\text{s}^{-1}=\frac{345\:\text{m}\cdot\text{s}^{-1}}{1+3{,}722\cdot10^{-14}} \end{equation*} Jmenovatel se v tomto případě liší od jedničky pouze o přibližně \(37\) biliardtin. Výsledná rychlost je potom přibližně \(344{,}999999999987\:\text{m}\cdot\text{s}^{-1}\). Oproti klasické předpovědi to je rozdíl o \(13\) biliontin metru za sekundu. Těžko tedy budeme tyto rozdíly pozorovat u běžných rychlostí v našich podmínkách na Zemi, a proto většinou velmi dobře vystačíme s klasickým skládáním rychlostí.
3.6 Nadsvětelné rychlosti
Rychlost světla je až nepředstavitelně velká. Proti téměř třem stům tisícům kilometrům za vteřinu je jakákoli rychlost, kterou zažíváme na naší planetě, nicotná. Pokud se vydáte na výlet tryskovým letadlem, jedním z nejrychlejších dopravních prostředků kdy vytvořených, dosáhnete podle tabulky výše necelých \(0{,}00009\:\%\) rychlosti světla. Technologie se ale pořád vyvíjí kupředu a minimálně při kosmických letech bychom měli dosahovat stále větších rychlostí. Můžeme ale někdy dosáhnout rychlosti světla?
Všechny naše dosavadní závěry o speciální relativitě se zdají být namířeny proti této možnosti. Matematické argumenty proti plynou z Lorentzovy transformace, z níž jsme odvodili dilataci času a kontrakci délek. Reálný objekt pohybující se rychlostí světla by se nám jevil nekonečně zkrácený ve směru svého pohybu a jeho hodiny by se zastavily, čas by pro něj prakticky neexistoval. To není představa, se kterou bychom se dokázali u reálných hmotných objektů nějak lehce vyrovnat. Pro nadsvětelné rychlosti také nejde matematický aparát LT použít, protože dostáváme pod odmocninou záporné číslo. Nicméně, tomuto sporu se můžeme vyhnout tvrzením, že Lorentzova transformace je nástroj pro počítání pouze s podsvětelnými rychlostmi, respektive se vztažnými soustavami, které se pohybují vůči sobě navzájem pomaleji než světlo. Může být tedy pouze omezeným nebo nedokonalým nástrojem a skutečnost, že neumí popsat nadsvětelné rychlosti, ještě neznamená, že nejsou možné. Potřebujeme tedy pádný fyzikální argument.
V rovnici \eqref{3.11} jsme uvedli relativisticky správnou verzi hybnosti a z ní jsme odvodili pro jednoduchý případ přímočarého zrychlování rovnici \begin{equation*}\tag{3.19}\label{3.19} \vec{F}=\gamma^3m_0\vec{a}, \end{equation*} ze které můžeme vyjádřit zrychlení jako \begin{equation*}\tag{3.20}\label{3.20} \vec{a}=\frac{\vec{F}}{\gamma^3m_0}=\frac{\vec{F}}{m_0}\left(1-\frac{v^2}{c^2}\right)^3. \end{equation*} Pokud budeme na těleso působit silou, dodáme mu zrychlení. Na to jsme zvyklí z klasické fyziky a platí to i v relativitě. V rovnici \eqref{3.20} ale vidíme, že se zvětšující se rychlostí budou účinky působící síly ubývat a abychom například udržovali raketu na konstantním zrychlení, museli bychom působit čím dál větší silou. Jinými slovy, jak se zvětšuje rychlost tělesa, je stále těžší ho urychlovat. Vyžaduje to čím dál tím větší sílu, a jak by se rychlost tělesa blížila k rychlosti světla, působící síla a tím pádem i množství vynaložené energie musí nutně jít do nekonečna. Taková situace ale nastat nemůže, protože nemáme k dispozici nekonečné množství energie, abychom tělesa na rychlost světla urychlili. Nicméně teoreticky se této hranici dokážeme přiblížit libovolně blízko. Koneckonců, například protony dokážeme, jak už bylo řečeno výše, ve velkých urychlovačích urychlit na rychlosti velmi blízké rychlosti světla. Zmiňovali jsme konkrétní případ rychlosti \(99{,}9999991\:\%\:c\) a toto číslo se bude jistě dále čím dál více přibližovat \(100\:\%\). Každé další přiblížení je ale stále energeticky náročnější a přesně rychlosti světla dosáhnout podle STR nemůžeme, natož abychom ji překročili.
Dalším náznakem, na který jsme narazili, byl fakt, že ani skládáním podsvětelných rychlostí se nedostaneme nad rychlost světla. Víme, že rychlost objektu je relativní, závisí na inerciální soustavě, ze které ho pozorujeme. I když se ale nemusí jednotliví inerciální pozorovatelé na rychlosti daného objektu shodnout, díky relativistickému skládání rychlostí platí, že pokud se objekt pohybuje podsvětelnou rychlostí v jedné inerciální soustavě, pohybuje se pomaleji než světlo ve všech inerciálních soustavách.
Pokud má tedy STR pravdu (a zatím se zdá, že ano), není možné se dostat z podsvětelné rychlosti na rychlost světla nebo i nad ní. Zatím ale z žádného argumentu přímo nevyplývá, že by se něco (schválně se zde vyhýbáme slovu částice nebo předmět) nemohlo pohybovat čistě nadsvětelnými rychlostmi.
Hlavním důvodem, proč se nám nezamlouvá pohyb nadsvětelnou rychlostí, je zachování kauzality. Kauzalita znamená vztah mezi příčinou a jejím důsledkem. Konkrétně nás zajímá pořadí, ve kterém dvě kauzálně svázané události nastanou. Nejdříve by se měla odehrát příčina a pak teprve nastat důsledek a na tomto pořadí by se měli shodnout všichni pozorovatelé. Ukažme nyní, že cestování nadsvětelnou rychlostí by mohlo kauzalitu událostí narušit.
Vzpomeňme si na události \(U_1,U_3\) a \(U_4\), které jsme používali výše. \(U_1\) byl průlet jedné kosmické lodi kolem Země a této události jsme v soustavě Země přiřadili souřadnice \(U_1=[0\:\text{s},0\:\text{m}]\). \(U_3\) byl příchod světelného (či spíše elektromagnetického) signálu, který vyslala Země při \(U_1\), na Mars (například o tom, že kosmická loď je na cestě). \(U_4\) byla libovolná událost, která se odehrála na Marsu z pohledu Země \(60\:s\) po \(U_1\), tedy \(U_4=[60\:\text{s},54,6\cdot10^9\:\text{m}]\). Ukázali jsme, že prostoročasový interval mezi \(U_1\) a \(U_4\) je prostorupodobný, což znamená, že nic pohybující se rychlostí světla (například elektromagnetický signál) nebo pomaleji nemůže být přítomno oběma událostem. Představme si nyní, že lidé vynalezli nadsvětelný způsob komunikace, který se šíří rychleji než světlo, a současně s událostí \(U_1\) vyšle Země na Mars zprávu i tímto způsobem. \(U_4\) pak bude událost přijetí této zprávy na Marsu. Snadno si spočítáme, že aby to byla pravda, signál by se musel pohybovat z pohledu Země rychlostí \begin{equation*} \bar{v}=\frac{\Delta{}x}{\Delta{}t}=\frac{54{,}6\cdot10^9\:\text{m}}{60\:\text{s}}=9{,}1\cdot10^8\:\text{m}\cdot\text{s}^{-1}\doteq3{,}04\:c. \end{equation*} Zatím se nic podivného neděje. Oběma signály obdrží Mars zprávu o blížící se raketě, jen nadsvětelným signálem to bude dříve. Nikdo na Zemi ani Marsu nepochybuje, že nejdříve byly signály vyslány Zemí (událost \(U_1\)) a následně zachyceny Marsem (události \(U_3\) a \(U_4\)). Problém ale nastane, když se na situaci podíváme z jiné perspektivy, konkrétně z pohledu první kosmické lodi (čárkovaná soustava). Připomeňme si nyní tabulku 3.3, respektive její část:
| Tabulka 3.3a Výřez tabulky 3.3 | ||||
|---|---|---|---|---|
| Události | Vzt. soustava | \(\Delta{}t/\text{s}\) | ||
| \(U_1 \rightarrow U_3\) | \(S\) | \(182\) | ||
| \(S^\prime\) | \(\boldsymbol{60{,}7}\) | |||
| \(S^{\prime\prime}\) | \(129{,}2\) | |||
| \(U_1 \rightarrow U_4\) | \(S\) | \(60\) | ||
| \(S^\prime\) | \(\boldsymbol{-142{,}7}\) | |||
| \(S^{\prime\prime}\) | \(0\) | |||
Vidíme, že v čárkované soustavě je mezi událostmi \(U_1\) a \(U_3\) stále kladný časový interval, což v naší konvenci znamená, že událost \(U_1\) se stane z pohledu lodi první a přibližně za \(60{,}67\:\text{s}\) následuje \(U_3\) (čas mezi událostmi je pochopitelně pro posádku lodi kratší). Na druhou stranu časový interval mezi \(U_1\) a \(U_4\) nám z pohledu první lodi vyšel záporný, tedy první se udála \(U_4\). Dokud byla \(U_4\) náhodná a na ničem nezávislá událost, toto přehození ničemu nevadilo. Nyní ale dostáváme velmi podivný výsledek, že z pohledu posádky lodi nejprve dorazil nadsvětelný signál na Mars a poté byl teprve vyslán ze Země, jakoby se signál vracel v čase. Nejde tu ani o žádnou iluzi, podle naší teorie tímto způsobem skutečně posádka lodi události naměří. Vidíme tedy, že připuštění signálu šířícího se nadsvětelnou rychlostí vede k porušení kauzality (a stejný argument by platil i pro pohyb libovolných částic a těles). Různí inerciální pozorovatelé by se neshodli na pořadí příčiny a důsledku, čímž vyvstává celá řada koncepčních problémů a spekulací ohledně cestování časem. Zachování kauzálního propojení událostí je patrně asi nejsilnějším argumentem, díky kterému bychom k nadsvětelným rychlostem měli být přinejmenším silně skeptičtí.
Dovolme si ještě jednu důležitou poznámku. Lorentzovu transformaci, ze které všechny naše závěry plynuly, lze odvodit místo invariance rychlosti světla alternativně předpokladem, že existuje jistá maximální možná rychlost šíření informace, na které se všichni inerciální pozorovatelé shodnou (je invariantní vůči změně inerciální soustavy). Pokud by se neshodli, existovala by preferovaná soustava, kde by byla tato rychlost největší, a narušili bychom ekvivalenci všech inerciálních systémů. Tato rychlost může být buď konečná, nebo nekonečná. Nekonečná vede na klasickou mechaniku a Galileiho transformace. Pro konečnou bychom dostali úplně stejné vztahy, kde by místo \(c\) figuroval nějaký neznámý vesmírný rychlostní limit, řekněme \(d\). Z experimentů by pak ale nezbytně vyplynulo, že \(d=c\), tj. že tato maximální možná rychlost je zároveň právě rychlost světla ve vakuu. Je zajímavé, že z hlediska rychlosti šíření můžeme rozdělit známé fyzikální jevy či objekty na dvě skupiny. Hmotné částice či tělesa z nich vytvořená se pohybují podsvětelnými rychlostmi, zatímco nehmotné „objekty“ (tj. objekty s nulovou klidovou hmotností) jako elektromagnetické vlnění (fotony), gravitační vlny či gluony, tj. částice zprostředkovávající silnou jadernou interakci, se pohybují vždy rychlostí světla. V době psaní tohoto textu (jaro 2020) je hmotnost gluonů teoreticky odhadována jako nulová a z experimentů vyplývá, že je určitě menší než řádově \(10^{-39}\:\text{kg}\).
Shrnutí třetí části
Speciální teorie relativity se zabývá inerciálními soustavami a vztahy mezi nimi. Je založena na dvou postulátech:
- Princip relativity – Fyzikální zákony nabývají stejného tvaru pro všechny inerciální pozorovatele.
- Princip konstantní rychlosti světla – Rychlost světla ve vakuu je pro všechny inerciální pozorovatele stejná v každém směru a světlo se pohybuje rovnoměrně přímočaře.
Transformace souřadnic, která splňuje základní postuláty, se nazývá Lorentzova (LT) a pro dvě soustavy navzájem se pohybující rychlostí \(v\) ve směru svých \(x\)-ových os platí \begin{equation*} t^\prime=\frac{t-\frac{vx}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}} \quad x^\prime=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}} \quad y^\prime=y \quad z^\prime=z, \end{equation*} kde \(c\) je rychlost světla ve vakuu.
Výraz \(1/\sqrt{1-\frac{v^2}{c^2}}\) se v STR objevuje tak často, že má své vlastní označení γ a říká se mu Lorentzův faktor nebo jednoduše gama faktor. Z matematického hlediska je mnoho zajímavých fyzikálních jevů v STR způsobeno právě tímto faktorem.
Ve speciální relativitě je výhodné dívat se na prostor a čas jako na jeden celek, tzv. prostoročas. Popisujeme ho nejčastněji pomocí souřadnic \((t,x,y,z)\). Každá taková čtveřice souřadnic určuje vzhledem k dané inerciální soustavě událost (tj. konkrétní místo a konkrétní čas).
Z LT plynou nové důsledky pro naše vnímání okolního světa. Pokud se bude vzhledem k nám někdo pohybovat nenulovou rychlostí, jeho čas bude oproti našemu zpomalen (dilatace času) a daná osoba bude pro nás zkrácená ve směru pohybu (kontrakce délek). Jde ale o relativní efekty, které na sobě druhý pozorovatel sám nepociťuje, naopak pro něj budeme my ti s pomalejším časem a zkrácenými délkami.
Na Zemi v běžných situacích efekty STR nepozorujeme, protože naše rychlosti jsou příliš malé v porovnání s rychlostí světla a relativistické efekty jsou zanedbatelně malé. Pro rychlosti blízké rychlosti světla, zejména v částicové fyzice, může obecně docházet k velkým rozdílům oproti předpovědím klasické fyziky.
Právě částicová fyzika je spolu s astrofyzikou jedním z nejlepších způsobů, jak experimentálně prověřovat platnost STR. Aktuálním příkladem je Velký hadronový urychlovač (LHC). Již přes sto let nebyl zjištěn rozpor mezi reálným chováním přírody a speciální relativitou (pokud tedy neuvažujeme i gravitaci, jak uvidíme v další části).
Na čem se všichni inerciální pozorovatelé shodnou, je prostoročasový interval mezi dvěma událostmi, jehož kvadrát je dán vztahem \begin{equation*} (Δs)^2=-c^2 (Δt)^2+ (Δx)^2+(Δy)^2+(Δz)^2. \end{equation*} Interval nazveme časupodobný, pokud je jeho druhá mocnina menší než nula. Spojuje dvě události, mezi kterými je možné doputovat podsvětelnou rychlostí. Interval s kvadrátem větším než nula nazýváme prostorupodobný, spojuje události, které se nemohou navzájem reálně ovlivnit, protože by bylo potřeba nadsvětelné rychlosti. Mezním případem je nulový nebo světlupodobný interval, který odpovídá pohybu mezi událostmi rychlostí světla.
Klasické skládání rychlostí nevyhovuje postulátům STR. Z Lorentzovy transformace plyne nové pravidlo pro skládání rovnoběžných rychlostí \begin{equation*} v=\frac{v^\prime+V}{1+\frac{Vv^\prime}{c^2}}, \end{equation*} kde \(V^\prime\) je rychlost předmětu, kterou má v čárkované soustavě, jež se vůči nám pohybuje rychlostí \(v\). \(V\) je pak rychlost předmětu, kterou naměříme my. V případě, kdy jsou rychlosti \(V^\prime\) a \(v\) opačného směru, v čitateli i jmenovateli se objeví mínus. Tímto způsobem nelze nikdy překročit rychlost světla, ani složením dvou rychlostí velmi blízkých \(c\).
Hlavním důvodem, proč nepovažujeme nadsvětelné rychlosti za možné, je porušení kauzality, jasného určení dvou událostí jako příčiny a důsledku. Z pokusů a teorie vyplývá, že vše s nenulovou klidovou hmotností se může pohybovat pouze podsvětelnými rychlostmi a částice bez klidové hmotnosti se pohybují rychlostí světla.
Příklady k třetí části
Cesta do nejbližší sluneční soustavy
Nejbližší hvězdný systém je Alfa Centauri, vzdálený \(4{,}365\) světelného roku. Vyšleme k němu raketu konstantní rychlostí \(0{,}5\:c\) vůči Zemi (opět budeme uvažovat jen průlety rakety startem a cílem, tj. bez zrychlování). Spočítejte, za jak dlouho pro nás na Zemi dorazí raketa ke svému cíli, kolik času uplyne pro posádku rakety a jak dlouhá se bude vzdálenost k cíli posádce jevit. Výsledky nám stačí v letech a světelných rocích, takže je zbytečné při výpočtu převádět na základní jednotky.
Z pohledu Země bude cesta trvat \(8{,}73\) roku, pro posádku rakety pouze přibližně \(7{,}56\) roku. Vzdálenost k Alfa Centauri se zároveň vzhledem k posádce zkrátí na asi \(3{,}78\) světelného roku.
Relativistická atletika
Vžijme se na chvíli do role pedantického atletického rozhodčího. Poté, co jsme si přečetli o speciální relativitě a změnách, které přináší do našeho chápání času a prostoru, bychom rádi zjistili, jestli náhodou není třeba i v atletice začít používat STR. Nejrychleji se pohybují sprinteři při závodu na \(100\:\text{m}\), takže se v našem rozboru omezíme na tuto disciplínu. Jako příklad si vezmeme světový rekord v běhu na \(100\:\text{m}\) Usaina Bolta z roku 2009, který byl \(9{,}58\:\text{s}\). Tyto údaje jsou samozřejmě naměřeny na stadionu, v soustavě spojené se zemí. V řeči STR, mezi dvěma událostmi (start závodu a proběhnutí cílem) uběhl v naší klidové soustavě čas \(\Delta{}t=9{,}58\:\text{s}\). Prostorově dělí události vzdálenost \(\Delta{}x=100\:\text{m}\). Dovolíme si na tomto místě malé zjednodušení a panu Boltovi přiřadíme jeho průměrnou rychlost \(v=\Delta{}x/\Delta{}t\). I když je jasné, že ve skutečnosti neběží pořád stejně rychle, jelikož se musí dostat co nejrychleji z nuly na svou maximální možnou rychlost. Zkuste nyní spočítat, kolik času uběhne pro pana Bolta během jeho idealizovaného závodu a jakou vzdálenost podle svého měření skutečně uběhne (pozor, díky malé rychlosti půjde o extrémně malé rozdíly, takže budete potřebovat kalkulačku, která zvládne hodně desetinných míst).
Z pohledu pana Bolta uběhne během závodu přibližně \(9{,}579999999999993\:\text{s}\) a závodní dráha se mu zkrátí na \(99{,}99999999999993\:\text{m}\).
Vesmírná přestřelka
Dvě znepřátelené vesmírné lodě se utkaly v bitvě. První z nich se pohybuje rychlostí \(0{,}01\:c\) vzhledem k protivníkovi a vypustí torpédo ze svého pohledu rychlostí \(0{,}4\:c\). Druhá loď zaregistruje vystřelení torpéda na svých elektromagnetických senzorech 5 sekund svého času po jeho vypuštění. K provedení úhybného manévru potřebuje druhá loď alespoň 10 sekund svého času. Za předpokladu, že automaticky začne manévr v momentě, kdy zaregistruje blížící se torpédo, stihne se mu vyhnout? Zkuste postupovat následujícím způsobem:
- Počítejte v klidové soustavě druhé lodi. Jak daleko od ní došlo k vypuštění torpéda, jestliže se k ní informace dostávala 5 sekund (předpokládáme, že její senzory zachycují elektromagnetické záření).
- Jakou rychlostí se přibližuje torpédo k druhé lodi? Jinými slovy, jakou má torpédo rychlost v soustavě spojené s uhýbající lodí?
- Jakou vzdálenost urazilo torpédo za 5 sekund, než se o něm posádka lodi dozvěděla? Kolik mu tím pádem zbývá k cíli?
- Za jak dlouho urazí tuto zbývající vzdálenost?
K vypuštění torpéda došlo ve vzdálenosti \(5\:\text{s}\cdot3\cdot10^8\:\text{m}\cdot\text{s}^{-1}=15\cdot10^8\:\text{m}\). To se blíží k lodi rychlostí zhruba \(0{,}408\:c\) (vidíme, že rychlosti ještě nejsou tak velké, aby relativistické skládání rychlostí dalo dost odlišný výsledek od klasického). Za dobu pěti sekund tak urazilo torpédo vzdálenost \(6{,}12\cdot10^8\:\text{m}\). K cíli mu tím pádem zbývá \(8{,}88\cdot10^8\:\text{m}\), což svou rychlostí urazí za přibližně \(7{,}25\:\text{s}\). Vesmírná loď tedy nestihne provést úhybný manévr včas.
Rozpad kaonu \(K^+\)
Kaon \(K^+\) je elementární částicí s průměrnou dobou života \(12{,}38\:\text{ns}\), naměřenou v jeho klidové soustavě. V laboratoři jsou generovány kaony o rychlosti \(99\:\%\) rychlosti světla. Jaký bude průměrný dolet kaonů? Proveďte klasický i relativistický výpočet a porovnejte.
Klasicky vzato, průměrná dráha doletu kaonů bude čistě násobek jejich rychlosti a doby života. Vychází přibližně \(3{,}67\:\text{m}\). Podle speciální relativity bude čas kaonů oproti laboratorní soustavě dilatovaný, do výpočtu musíme zahrnout ještě příslušný gama faktor. Po dosazení dostáváme přibližně \(26{,}05\:\text{m}\). Tento markantní rozdíl je snadno měřitelný a podobné experimenty s částicemi jsou prováděny již desítky let.
Různé soustavy a události
Jako naši klidovou soustavu si vezměme soustavu Slunce-Země, s počátkem souřadnic na povrchu Slunce. Pro jednoduchost umístíme Zemi na osu \(x\) a na chvíli zapomeneme na její oběh kolem Slunce (což můžeme udělat, pokud naše úvahy nebudou zahrnovat příliš dlouhé časy) a stejně tak pohyb Slunce samotného v rámci naší galaxie. Vezměme si dvě události v této inerciální soustavě. Události \(U\) – erupci na Slunci – přiřadíme souřadnice \(t_U=0\:\text{s}\) a \(x_U=0\:\text{m}\) (protože se v našem jednoduchém nastavení soustavy nebudou měnit souřadnic \(y\) a \(z\), budeme je v tomto příkladu vynechávat). Událost \(V\) bude zpozorování světelného záblesku z této erupce na Zemi. Přibližná průměrná vzdálenost Slunce-Země v jejich klidové soustavě je 150 miliónů kilometrů, tedy \(150\cdot10^6\:\text{km}=15\cdot10^{10}\:\text{m}\). Použijeme-li přibližnou hodnotu rychlosti světla ve vakuu \(3\cdot10^8\:\text{m}\cdot\text{s}^{-1}\), doba letu signálu a zároveň okamžik jeho dopadu v naší soustavě je \begin{equation*} t_V=\frac{15\cdot10^{10}\:\text{m}}{3\cdot10^8\:\text{m}\cdot\text{s}^{-1}}=500\:\text{s}=8\:\text{min}\:20\:\text{s}. \end{equation*} Naše události tedy mají v inerciální soustavě Slunce-Země souřadnice \(U[0\:\text{s};0\:\text{m}]\) a \(V[500\:\text{s};15\cdot10^{10}\:\text{m}]\) a jednoduše zjistíme, že rozdíly souřadnic mezi událostmi jsou \(\Delta{}t=500\:\text{s}\) a \(\Delta{}x=15\cdot10^{10}\:\text{m}\). Vypočítejte:
- kvadrát prostoročasového intervalu mezi událostmi \(U\) a \(V\).
- časovou a prostorovou vzdálenost mezi událostmi, kterou naměří posádka lodi pohybující se ve směru spojnice Slunce-Země rychlostí \(0{,}5\:c\) vůči Zemi (pozor, je zde třeba použít celou Lorentzovu transformaci, protože raketa není přítomna oběma událostem).
- kvadrát prostoročasového intervalu mezi událostmi \(U\) a \(V\) v soustavě kosmické lodi.
- Jelikož události \(U\) a \(V\) jsou propojeny světelným signálem, příslušný čtyřinterval musí nutně vyjít nulový.
- \(\Delta{}x^\prime\doteq8{,}66\cdot10^{10}\:\text{m},\quad\Delta{}t^\prime \doteq288{,}68\:\text{s}\)
- Jelikož kvadrát čtyřintervalu je invariantní vůči transformaci do jiné inerciální soustavy, musím nám vyjíst stejně jako v bodě a) nulový.