Precese - pokračování
 Pokusme se nyní vysvětlit pohyb našeho roztočeného setrvačníku pověšeného na niti.
Tento setrvačník není volný, protože na něj působí jednak tíhová síla v těžišti směrem dolů a jednak tahová síla nitě na konci osy směrem nahoru,
viz obr. 5. Jestliže si zavedeme soustavu souřadnic s počátkem na konci osy, kde je k setrvačníku přivázaná nit, je těžiště setrvačníku určeno vektorem r
a moment tíhové síly Fg vzhledem k počátku soustavy souřadnic určíme ze vztahu |
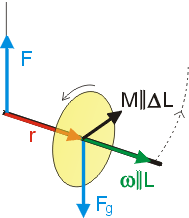
obr. 5: setrvačník na niti |
|
. |
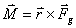(56) |
Vektor momentu tíhové síly je tedy kolmý na oba vektory r a Fg a jeho orientaci můžeme určit pomocí pravidla pravé ruky.
Druhá věta impulsová říká, že změna momentu hybnosti setrvačníku je rovna momentu síly působící na setrvačník. Jestliže zanedbáme
zpomalování rotace setrvačníku vlivem tření, zůstává velikost jeho momentu hybnosti konstantní a musí se tedy měnit směr momentu hybnosti, tedy i směr osy rotace vůči zvolenému počátku
soustavy souřadnic.
Vektor změny momentu hybnosti má stejný směr jako vektor momentu síly M, a setrvačník se proto bude otáčet
ve vodorovné rovině kolem bodu zavěšení na konci osy, viz obr. 5.
|
|
Popsanému pohybu setrvačníku se říká precese a můžeme ho také pozorovat například u roztočené „káči“. (jako „káča“ může sloužit například
náš vyrobený setrvačník z CD, viz podrobnosti, který budeme roztáčet mezi prsty). Jakmile „káča“ nerotuje přesně ve svislém směru, působí
na ni moment tíhové síly a osa rotující „káči“ v důsledku druhé věty impulsové opisuje povrch precesního kužele obráceného špičkou dolů.
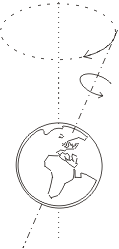
Také Země tvoří velký setrvačník se skloněnou osou, a protože není ideálně kulová, působí na ni Slunce a Měsíc silovým momentem. To způsobuje takzvanou lunisolární
precesi, která způsobuje, že zemská osa nemíří stále stejným směrem, ale jednou za platonský rok (25 700 let) opíše dokola povrch precesního kužele. Jestliže dnes míří
Zemská osa přibližně k Polárce, za 14 000 let budeme sever určovat podle hvězdy Vega v souhvězdí Lyry. |
|
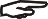Pokusme se určit, jak velká je rychlost precesního pohybu setrvačníku.
Uvažujme setrvačník s momentem setrvačnosti J zavěšený na konci jeho osy tak, že osa svírá se svislým směrem úhel j.
Délka poloviny osy (od místa uchycení k těžišti) je l a setrvačník rotuje s úhlovou rychlostí w.
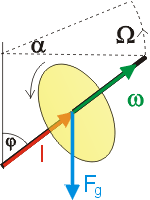
Velikost vektoru změny momentu hybnosti můžeme vyjádřit jako |
|
|
. |
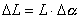(57) |
L je konstantní velikost momentu hybnosti daná vztahem L = Jw,
Da je změna úhlu osy
ve vodorovné rovině - tedy úhel natočení osy vlivem precese.
Velikost momentu tíhové síly setrvačníku vzhledem k bodu uchycení určíme
jako
|
, |
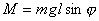(58) |
kde m je hmotnost setrvačníku, g je tíhové zrychlení.
Z druhé věty impulsové vyplývá:
|
|
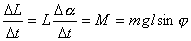
(59) |
Časová změna úhlu a vyjadřuje úhlovou rychlost precesního pohybu W, pro kterou dostáváme s využitím L = Jw výsledný vztah:
|
|
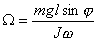
(60) |
Z tohoto vztahu je patrné, že úhlová rychlost precese je nepřímo úměrná úhlové rychlosti rotace setrvačníku. O tom se můžeme přesvědčit snadno
pokusem. Rychle roztočený setrvačník se otáčí dokola vlivem precese jen pomalu, jakmile se začne rychlost rotace zmenšovat, setrvačník se to „snaží vykompenzovat“ rychlejší precesí.
Na obsah
