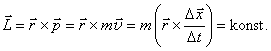FyzWeb - srážky a rotace

Kepler a Newton

Johannes Kepler zformuloval své zákony pouze na základě pozorování pohybu planet. Teprve Isaac Newton vyslovil hypotézu, že pohyb planet je ovlivněn gravitační silou – stejnou silou, která nás shodí na zem, když zakopneme.

Určitě si vzpomenete, že podle Newtona se každá dvě hmotná tělesa přitahují stejně velkými silami opačného směru. Velikosti těchto sil lze vypočítat ze vztahu

(61)

kde k = 6,67 . 10^-11 N.m².kg^-2 je gravitační konstanta, m, M jsou hmotnosti uvažovaných těles a r je vzdálenost středů těchto těles. Z uvedeného gravitačního zákona tedy například plyne, že tužka položená na stole přitahuje Zemi stejně velkou silou jakou přitahuje Země tužku.

Newton odvodil vztah (61) právě z Keplerových zákonů. Ukázal, že pokud se planety pohybují po eliptických drahách, závisí gravitační síla mezi nimi a Sluncem nepřímo úměrně na druhé mocnině jejich vzdálenosti. Poněkud složitějším výpočtem (uvedeným například v [6]) bychom mohli dokázat také opačné tvrzení: pokud na těleso působí centrální síla popsaná vztahem (61), pohybuje se toto těleso po elipse nebo kružnici, při vyšších rychlostech přejde tato dráha na parabolu, eventuelně hyperbolu.

? Je možné na pohyb planet aplikovat některé vztahy, které jsme zkoumali v souvislostí s rotací těles?

Uvažujme planetu (například naši Zemi) pohybující se po eliptické dráze kolem Slunce. Země rotuje kolem Slunce a měla by pro ni tedy platit druhá věta impulsová (52). Gravitační síla, kterou působí Slunce na Zemi míří ve směru spojnice Země Slunce a proto je její moment daný vztahem (56) nulový M = 0.

To ale znamená, že moment hybnosti Země vůči Slunci je konstantní - L = konst. - podobně jako v případě rotujícího krasobruslaře. Můžeme tedy psát:

(62)

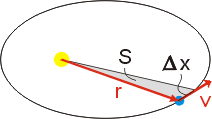
r je polohový vektor Země vzhledem ke slunci, p je hybnost Země, m a v jsou její hmotnost a rychlost, Dx je posunutí Země za čas Dt.

Z vlastností vektorového součinu vyplývá (viz podrobnosti), že vektorový součin r a posunutí Dx je úměrný ploše S opsané průvodičem planety, a ze vztahu (62) je vidět, že tato plocha je za konkrétní jednotku času konstantní.

(63)

Vidíme tedy, že Kepler svým druhým zákonem v podstatě vyjádřil zákon zachování momentu hybnosti - dlouho před jeho matematickou formulací.

? Jak vysvětlíme zvláštní poměr vzdáleností a oběžných dob v třetím Keplerově zákonu?

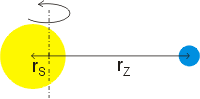
Doposud jsme mlčky předpokládali, že Země rotuje kolem Slunce. To není úplně přesné, spíše bychom měli říci, že rotují kolem společného hmotného středu – stejně jako dvě děti, které se drží za ruce a rychle se otáčejí kolem sebe. Čím těžší je jedno z dětí, tím blíže k němu je společná osa otáčení. Protože je Slunce zhruba 300 000 krát těžší než Země, je společná osa rotace mnohem blíže středu Slunce.

Předpokládejme zjednodušeně, že Země a Slunce kolem sebe obíhají po kruhových trajektoriích. Vzdálenost Slunce od společné osy otáčení je r_S, vzdálenost Země od této osy r_Z. Vzdálenost středů Slunce a Země r = r_S + r_Z je tedy konstantní.

Pro oběh Slunce kolem společného středu zapíšeme rovnost gravitační a odstředivé síly ve tvaru

(64)

kde m a M jsou hmotnosti Země a Slunce, T je doba jednoho oběhu (jeden rok). Stejně vyjádříme rovnost gravitační a odstředivé síly působící na Zemi:

(65)

Vykrácením M ve vztahu (64) a m v (65) a sečtením obou vztahů dostáváme

(66)

odtud

(67)

Poměr druhé mocniny oběžné doby Země a třetí mocniny vzdálenosti od Slunce je tedy konstantní. Pro libovolnou jinou planetu (například Jupiter) bychom stejným způsobem obdrželi na pravé straně vztahu (67) konstantu, která by se lišila pouze hmotností m dané planety. Hmotnost libovolné planety je však mnohem menší než hmotnost Slunce, proto vychází konstanta ve vztahu (67) pro všechny planety přibližně stejná, což vyjadřuje třetí Keplerův zákon.

Výsledek, který jsme odvodili pouze pro kruhový pohyb planet, platí i pro obecný eliptický pohyb, jestliže vzdálenost r nahradíme délkou velké poloosy elipsy. Odvození je však poněkud obtížnější.

Keplerovy zákony potom můžeme použít pro pohyb libovolného tělesa v gravitačním poli mnohem hmotnějšího tělesa.

Pokuste se například vyřešit následující úlohu:

Jak dlouho bude trvat cesta kosmické lodě ze Země k Jupiteru? Abychom využili gravitační pole Slunce, naplánujeme cestu tak, aby loď opsala polovinu eliptické trajektorie se Sluncem v jednom ohnisku.

Jakou rychlost musíme v takovém případě udělit lodi při startu z oběžné dráhy Země? Řešení

<< Keplerovy zákony

Volná osa rotace >>

Na obsah