|
FyzWeb články |
||||
Pokud jste někdy zkusili ukázat, jak vlastně kapka vzniká, zjistili jste, že i když velmi zpomalíte přítok vody, samotné odtržení kapky je rychlejší, než dokážeme pozorovat. Sedmý díl naší série proto věnujme právě tomu, jak kapka vzniká, trhá se a co všechno na ní můžeme pozorovat. Jak se tvoří kapka
Po odkápnutí předchozí kapky se nejprve sbírá voda podél vodovodu jako by voda vzlínala podél celé spodní plochy. Když začne být vody více a tíhová síla začne převažovat, objeví se v jednom (zřejmě nejnižším) místě zakřivení - zárodek kapky držený pohromadě povrchovou silou, který postupně narůstá, až jej povrchová síla neudrží a kapka se odtrhne. Až sem bychom k popisu tvorby kapky kameru vůbec nepotřebovali, její použití nám ale ukáže jevy, které bychom nejspíš nečekali. Především se jedná o tvar kapky, který není „kapkový", tak jak jej známe z dětských knížek, ale jedná se o pružnou kouli, která osciluje v důsledku napnutí povrchové vrstvy při odtržení podobně, jako by osciloval balonek naplněný vodou, natažený a puštěný. Druhým zajímavým místem je délka „vodní stopky," na které je kapka těsně před odtržením zavěšena - jde o několika (dvoj- či troj-) násobek průměru kapky. Pokud bychom měřili graf závislosti polohy těžiště kapky na čase a proložili do něj parabolu Překvapivá délka stopky, která se přeruší při odtržení kapky, má za následek to, že povrchové napětí nedokáže veškerou vodu obsaženou ve stopce vrátit zpět k vodovodu ani přitáhnout ke kapce, stopka se potrhá na několika místech najednou a vznikne jedna nebo více kapek velikosti zhruba o řád menší, než měla prvotní kapka. V přiloženém videozáznamu můžeme pozorovat vznik dvou až tří kapek pod ústím vodovodu. (Na tomtéž vodovodu byl děj natáčen opakovaně s obdobným výsledkem, nejedná se tedy o náhodný jev.)     Ještě překvapivější je to, co po vytvoření dvou kapek následuje - tyto kapky totiž na sebe narazí a namísto toho, aby se spojily do jedné větší, odrazí se od sebe. Znamená to, že se povrchová vrstva vody chová jako pružná blána nejen „dovnitř kapky," kterou stlačuje, ale i navenek. Takové chování povrchové vrstvy nelze ale vysvětlit pouze pomocí tzv. sféry molekulového působení, jak je tomu ve středoškolských učebnicích [1], ale nějakým složitějším způsobem. Z chování kapek je ale jasné, že má povrchová vrstva kapky podobné vlastnosti, jaká mají třeba mastná oka na polévce, která se spojí až poté, co lžící protrhneme jejich okraje, nebo lehká atomová jádra, která se ochotně slučují, ale musíme nejprve dodat značné množství energie, aby se k sobě dostala dostatečně blízko.
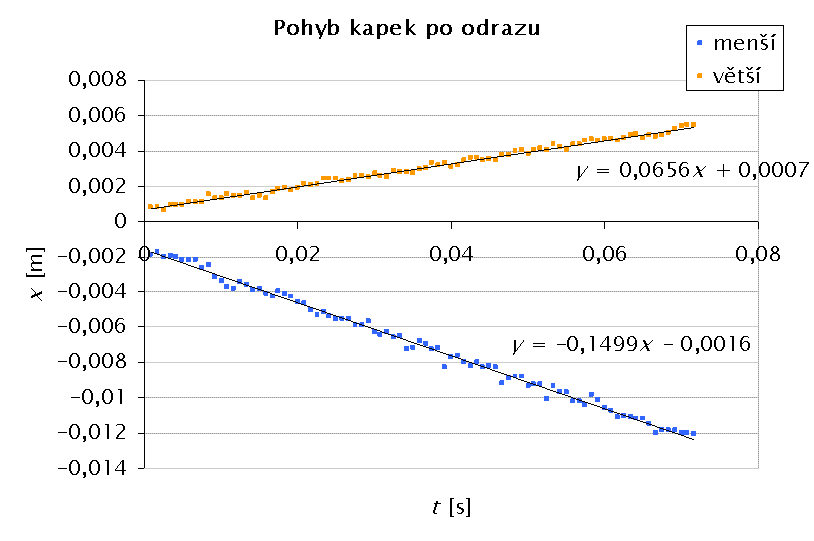
Na pádu a odrazu dvojice kapek můžeme ověřit i zákon zachování hybnosti ve směru osy x (v horizontálním směru). Obě dvě kapičky začínají s nulovou rychlostí ve směru x, horní má ale v důsledku povrchové síly před odtržením rychlost ve směru dolů a dolní obráceně ve směru nahoru. Kapky proto na sebe narazí, odrazí se, a protože ráz není centrální, odrazí se do stran.
V grafu vidíme vynesenou závislost polohy x obou kapek na čase t. V tomto směru je rychlost obou kapek konstantní. Z poměru rychlostí obou kapek a ze zákona zachování hybnosti vypočteme poměr jejich hmotností jako převrácenou hodnotu předchozího poměru. Druhý způsob, jakým můžeme určit poměr hmotností kapek, je změření jejich průměrů. Měření velikostí bylo provedeno vyjmutím několika snímků z videa, jejich vložením do grafického editoru a umístěním co nejlépe vyhovujících kružnic přes fotografie kapek. Navzdory tomu, že velikost kapek je pouze několik pixelů, můžeme tímto způsobem získat relativně přesné měření. Poměr hmotností by pak měl být třetí mocninou poměru průměrů. Např. pro data z grafu získáváme poměr horizontálních složek rychlosti 0,438:1, což znamená, že podle zákona zachování hybnosti by měl poměr hmotností být 2,283:1 a poměr poloměrů kapek 1,317:1. Poměr poloměrů kapek odměřený z videoklipu je 1,32:1, ve velmi dobré shodě. Zdroje a odkazy[1] K. Bartuška - E. Svoboda, Fyzika pro gymnázia - Molekulová fyzika a termika, 5. vyd., Praha: Prometheus, 2009, ISBN 978-80-7196-383-7 Použitá videa ke stažení
Další již zvěřejněné díly seriálu
Autory seriálu jsou RNDr. Jan Koupil a RNDr. Vladimír Vícha. | ||||
Odkapávání vodní kapky z byrety nebo ústí vodovodu je děj, který se nezdá být příliš rychlým (navíc jej můžeme zpomalit například tlačkou), ale pouze do chvíle, než se začneme zajímat o samotný okamžik odtržení kapky, kdy už fotoaparát nebo obyčejná videokamera nestačí. Tvorbu kapky můžeme natáčet buď na tenké trubičce (kapilára, pipeta) nebo na volné ploše (spodní okraj ústí vodovodu), proces se ale zásadně neliší.