|
FyzWeb síly |
|||||||||||||
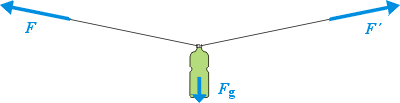
Více silAni ti nejsilnější z vás nedokáží zvednout dvoulitrovou láhev s vodou! Pokud s takovým tvrzením nesouhlasíte, vyzkoušejte si následující pokus. Dvoulitrovou láhev s vodou uvažte za hrdlo v polovině délky pevného provazu alespoň 5 metrů dlouhého (vhodná je například prádelní šňůra). Vyberte si někoho silného na pomoc, uchopte provaz (každý za jeden konec) a pokuste se láhev zvednout natažením provazu. Ať se budete snažit sebevíce, nepodaří se vám zvednout láhev tak, aby byl provaz zcela vodorovný. Nyní se můžete ohradit, že dokážete zvednout stejnou láhev normálně a budete mít samozřejmě pravdu. Proč ale zcela nezvednete láhev natažením provazu? Nakreslete si obrázek pokusu s lahví a vyznačte do něj síly, které se při pokusu uplatňují. Mohlo by to vypadat nějak takto: Fg představuje tíhovou sílu, kterou je láhev přitahována k zemi. Stejně velkou sílu bychom tedy museli vyvinout, abychom láhev zvedli normálním způsobem. F a F´jsou síly, kterými táhnou "siláci" za konce provazů. Všimněte si, že tyto síly jsou nakresleny rovnoběžně s provazem (nikoli například vodorovně od sebe). Musí to tak být vždy? Zkuste si nejdříve odpovědět sami a potom se podívejte na možné vysvětlení. Jak spolu souvisí síly na obrázku?
Máme tedy tři síly různého směru, které působí na hrdlo láhve. Pokud bychom chtěli tyto tři síly nahradit jedinou silou, bude mít nulovou velikost. Umíte vysvětlit, proč je tato výsledná síla (výslednice) působící na láhev nulová? Vysvětlení Tím, že jsme nahradili tři síly působící na láhev v jednom bodě jedinou výslednou silou, jsme tři původní síly takzvaně složili (také se říká, že jsme je vektorově sečetli). Co to přesně znamená skládat síly? Dvě síly se snadno skládají pokud míří stejným, nebo opačným směrem (pokud si je nakreslíme leží jejich vektory v jedné přímce). Pokud jste si vyrobili vlastní siloměry, nebo máte k dispozici třeba školní, vyzkoušejte si pomocí tří takových siloměrů skládání sil v jednom směru a pokuste se sami odhadnout, jaká pravidla pro takové skládání platí. Podrobnosti Výsledek pokusu by vám měl potvrdit to, co byste zřejmě hádali i bez pokusu. Složením dvou sil stejného směru obdržíme sílu mířící také tímto směrem. Velikost výsledné síly je přitom rovna součtu velikostí dvou skládaných sil, viz následující obrázek. Stejně by se skládalo i větší množství sil působících stejným směrem.
Výsledná zelená síla má stejný účinek, jako dvě původní síly. Při skládání dvou sil opačného směru má výslednice směr jako větší ze dvou skládaných sil ("větší síla přetáhne menší") a velikost výslednice je rovna velikosti větší síly mínus velikosti menší síly, viz následující obrázek. Výsledná síla míří ve směru větší z původních sil. Se skládáním sil v jednom směru si lidé často pletou takzvaný zákon
akce a reakce.
Jak si ale poradíme se silami mířícími různým směrem, jako v případě láhve na provaze?
Nyní se nám situace zjednodušila, protože místo sil různého směru máme pouze síly, mířící vodorovně nebo svisle, a ty umíme v každém tomto směru sčítat. Víme už, že součet sil působících na láhev ve vodorovném i svislém směru je nulový, protože láhev se nikam nepohybuje. To ale znamená, že složky Fx a Fx´ mají stejnou velikost a opačný směr a součet složek Fy a Fy´ má stejnou velikost jako síla Fg (pouze míří opačným směrem).
Určitě už tedy budete schopni vysvětlit, proč nelze láhev zvednout natahováním provazu tak, aby byl provaz zcela vodorovný. Vysvětlení
|
|||||||||||||




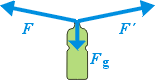 Silou F taháme za konec provazu, kousek provazu na konci tahá
za kousek před sebou a tak dále, až poslední kousek uprostřed provazu tahá
za láhev. Proto můžeme sílu F a stejně i F´ přenést
do jednoho bodu, ve kterém je uvázána láhev. Podobně přeneseme do tohoto
bodu sílu Fg .
Silou F taháme za konec provazu, kousek provazu na konci tahá
za kousek před sebou a tak dále, až poslední kousek uprostřed provazu tahá
za láhev. Proto můžeme sílu F a stejně i F´ přenést
do jednoho bodu, ve kterém je uvázána láhev. Podobně přeneseme do tohoto
bodu sílu Fg . Síla F míří mírně šikmo nahoru. Znamená to, že za
provaz taháme směrem k sobě a také trochu nahoru, viz obrázek vpravo. Těmto znázorněným
silám Fx a Fy se říká složky
síly F (F se z nich skládá). Můžeme tedy říct,
že jsme rozložili sílu F do dvou kolmých směrů (vodorovného
a svislého) na složky Fx a Fy
.
Stejně můžeme nahradit sílu F´ jejími složkami
Fx´ a Fy´.
Síla F míří mírně šikmo nahoru. Znamená to, že za
provaz taháme směrem k sobě a také trochu nahoru, viz obrázek vpravo. Těmto znázorněným
silám Fx a Fy se říká složky
síly F (F se z nich skládá). Můžeme tedy říct,
že jsme rozložili sílu F do dvou kolmých směrů (vodorovného
a svislého) na složky Fx a Fy
.
Stejně můžeme nahradit sílu F´ jejími složkami
Fx´ a Fy´. 