|
FyzWeb síly |
||||||||||||||
Páka
Která část bude těžší? Nebo budou obě stejně těžké? Asi je vám jasné, že uvedený problém nějak souvisí s takzvanou rovnováhou na páce, o které jste už určitě alespoň něco zaslechli. Pojďme si tedy připomenout, co vysvětluje tento jeden z vůbec prvních matematicky formulovaných fyzikálních zákonů.
Co musí platit pro závaží aby byla páka v rovnováze - tj. nepřeklápěla se? Pokud nevěříte virtuálnímu modelu (naprogramovat se dá cokoli) vyrobte
si vlastní jednoduchou páku a ověřte si své názory v reálných,
nefingovaných podmínkách.
Matematicky to můžeme vyjádřit jednoduchou rovnicí
kde F1 je velikost síly působící kolmo na páku ve vzdálenosti d1 od osy otáčení, F2 je velikost síly působící kolmo na opačné straně páky ve vzdálenosti d2 od osy otáčení. Vzdálenosti d1 se říká rameno síly F1, stejně vzdálenosti d2 rameno síly F2. Podívejme se na naši rovnici pro rovnováhu na páce ještě trochu podrobněji. Síla F1 se snaží otáčet pákou kolem její osy jedním směrem, F2 směrem opačným. Je-li páka v rovnováze (neotáčí se), můžeme říct, že otáčivé účinky obou těchto sil jsou stejně velké (pouze působí proti sobě). Víme už, že otáčivý účinek síly vyjadřuje veličina moment síly a rovnici pro rovnováhu na páce tedy můžeme zapsat jako
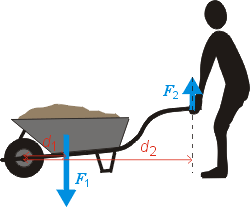
kde M1 je velikost momentu první síly, M2 síly druhé. Výrazy M1 = F1. d1 a M2 = F2 . d2 přitom přesně vyjadřují to, co už víme o momentu síly - že je tím větší, čím větší je síla a čím větší je její vzdálenost od osy otáčení. Ze zkušenosti určitě víte, že různé druhy pák využíváme každý den v mnoha zařízeních. Známým příkladem je třeba stavební kolečko, které možná používáte na zahrádce. Schematicky si ho můžeme představit jako jednoduchou páku, která se ale trochu liší od našeho modelového příkladu. Osa otáčení je totiž na konci páky (v ose kola) a obě síly proto působí na stejné straně. Také v tomto případě ale platí, že jedna síla otáčí pákou na jednu stranu (náklad tlačí kolečko směrem dolů), druhá síla otáčí páku opačným směrem (ruce zvedají kolečko nahoru). Naše pozorování tedy můžeme shrnout takto: Aby byla uvažovaná páka v rovnováze, musí být momenty sil, které na ni působí, stejně velké a navíc musí působit opačným směrem, aby se vzájemně vyrušily. Konkrétní velikost síly nebo délky ramene potom snadno spočítáme z rovnice pro páku. Představme si například, že na kolečku vezeme 80 kg těžký náklad. Jakou silou musíme zvedat rukojetě? Uvažujme například vzdálenosti (podle obrázku) d1 = 0,5 m, d2 = 1,6 m. Hmotnosti 80 kg odpovídá tíhová síla F1 = 800 N. Rukojetě tedy musíme zvedat silou:
Dovedete nyní odpovědět na úvodní otázku, která část vodorovně zavěšeného kmene stromu je těžší? Máte-li už problém dobře rozmyšlený, podívejte se na odpověď.
Zajímalo by vás jak těžký je nějaký drobný šperk, bonbón, knoflík,
nebo jiný lehký předmět?
|
||||||||||||||



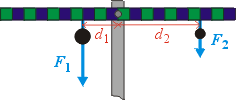 Pověsíme-li na
opačné strany páky po jednom závaží, je situace poměrně
jednoduchá. Stejně těžká závaží musí být stejně daleko od osy otáčení,
aby byla páka v rovnováze. Jestliže je jedno ze závaží těžší, musíme
jej posunout blíž k ose otáčení. Snadno se přesvědčíme, že dvakrát těžší
závaží na jedné straně musí být v poloviční vzdálenosti od osy, než závaží
na druhé straně, třikrát těžší závaží musí být třikrát blíže,
čtyřikrát těžší čtyřikrát blíže (ve čtvrtinové vzdálenosti) a tak
dále.
Pověsíme-li na
opačné strany páky po jednom závaží, je situace poměrně
jednoduchá. Stejně těžká závaží musí být stejně daleko od osy otáčení,
aby byla páka v rovnováze. Jestliže je jedno ze závaží těžší, musíme
jej posunout blíž k ose otáčení. Snadno se přesvědčíme, že dvakrát těžší
závaží na jedné straně musí být v poloviční vzdálenosti od osy, než závaží
na druhé straně, třikrát těžší závaží musí být třikrát blíže,
čtyřikrát těžší čtyřikrát blíže (ve čtvrtinové vzdálenosti) a tak
dále.