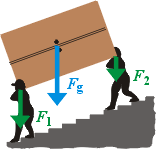
Složité rozkládání

Při pohledu na sloupy vysokého napětí můžeme obdivovat konstrukci vymyšlenou tak, aby snesla extrémní zatížení. Přesto se tyto pevné kolosy někdy mohou ohnout, a to pod tíhou obyčejné námrazy na vodičích, jako se to stalo například v sedmdesátých letech minulého století v obci Bystré ve Východních Čechách, viz foto dole vpravo.

Umíte vysvětlit, proč dokáže námraza ohnout pevné sloupy?

Spustit video - 1,3 MB

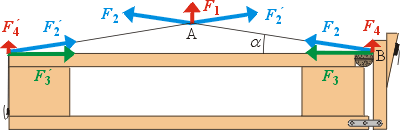
Pokud rádi louskáte vlašské ořechy, můžete si vyrobit netradiční louskáček, na kterém lze dobře sledovat vlastnosti skládání a rozkladu sil. Podrobnosti

Jak takový louskáček funguje?

Podívejme se, jaké síly se uplatňují při louskání ořechu pomocí našeho zařízení. Zatáhnutím za drát v jeho středu (v bodě A) na něj působíme silou F₁ směrem nahoru. Tato síla způsobí napnutí drátu, znázorněné v obrázku silami F₂ a F₂^´. Pozor, to neznamená, že v bodě A působí tři síly! To, co působí na drát, je pouze naše ruka (síla F₁), síly F₂ a F₂^´ jsou složkami síly F₁.

Síly se rozkládají na kolmé složky podle úhlu mezi lankem a rámem.

Rozložit sílu na dvě složky v daných směrech jednoduše znamená najít v těchto směrech takové dvě síly, jejichž složením (tj. vektorovým součtem) získáme původní sílu.

Z kapitoly O vektorech už víme, jak skládat síly pomocí vektorového rovnoběžníku, a velikost složek F₂ a F₂^´ můžeme tedy vypočítat jako:

kde a je úhel mezi lankem a horní latí rámu louskáčku. Při malém úhlu a bude síla F₂ mnohem větší než F₁, proto musí být drát dostatečně pevný, aby toto napětí vydržel.

Pravý konec napnutého drátu působí na dřevěný hranolek v bodě B silou F₂, kterou rozložíme do kolmých složek F₃ a F₄. Složka F₃ konečně představuje sílu působící na ořech a složku F₄ musíme vykompenzovat přidržením louskáčku na stole. Velikost síly, působící na ořech při louskání, určíme jako:

Zcela stejným způsobem bychom určili velikost síly F₃^´, působící na ořech z druhé strany.

Pokud jste si dali práci s výrobou louskáčku, můžete si nyní změřit, jaká síla je potřeba k rozlousknutí vlašského ořechu a také si svůj výsledek ověřit pomocí osobní váhy. Podrobnosti

Všimněme si ještě jedné důležité drobnosti. Na ořech působí při louskání dvě stejně velké síly opačného směru F₃ a F₃^´. Jejich vektorový součet je nulový, proto se celý ořech nebude pohybovat. Protože ale ořech není ideálně tuhý, způsobí síly F₃ a F₃^´ jeho deformaci a prasknutí.

Možná vám výroba louskáčku, jehož funkce využívá jednoduchého rozkladu sil, přijde zbytečná a nepraktická. Jde opravdu spíše o model, který ukazuje a dovoluje změřit, jak souvisejí velikosti sil se svými složkami. Podíváte-li se však kolem sebe, určitě přijdete na spoustu příkladů, v nichž se využívá, nebo je potřeba nějakým způsobem počítat s rozkladem sil. Za všechny příklady můžeme uvést alespoň luk - nástroj, který mnohokrát doslova změnil dějiny a jehož sportovní využití má i dnes mnoho fandů. Stejný princip rozkladu sil však můžete využít také například k bourání zdí, nebo vyprošťování zapadlého auta. Podrobnosti

Možná už jste někdy stěhovali těžkou skříň po schodech a víte ze zkušenosti, že větší tíhu pociťuje člověk, který je více dole, viz vedlejší obrázek. Je pochopitelné, že zatížení obou nosičů F₁ a F₂ je způsobeno tíhou skříně.

Jak ale rozložíme tíhovou sílu F_g, působící ve středu skříně, na rovnoběžné složky F₁ a F₂, jestliže nemáme k dispozici žádný vektorový rovnoběžník?

Vezměte si dlouhé pravítko a položte na něj libovolné malé závaží, které máte po ruce (těžítko, krabičku špendlíků, malý kámen apod.). Podložte prsty konce pravítka a požádejte někoho, aby pomalu posouval závažím po pravítku na jednu a druhou stranu. Jeden konec pravítka můžete také podložit knihou a posouvat závažím sami.

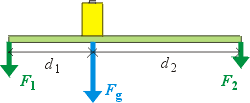
Jak se mění zatížení prstů při posouvání závaží?

Abyste toto zatížení změřili, položte jeden nebo oba konce pravítka na kuchyňskou nebo listovní váhu. Máte-li k dispozici delší pevné prkno, můžete použít jako závaží sami sebe a konce prkna podložit osobní váhou.

Vypozorujte sami pravidlo, podle kterého se rozkládá tíha závaží na dvě rovnoběžné složky na koncích pravítka. Nápověda

Nyní se pokusíme ověřit, zda experimentálně zjištěné pravidlo souhlasí s teoretickými principy. Složky F₁ a F₂ mají nahradit sílu F_g. To znamená, že musí mít na naši soustavu pravítka se závažím stejný posuvný i otáčivý účinek jako síla F_g (hmotnost pravítka zanedbáme). První podmínka bude splněna, jestliže vektorový součet sil F₁ a F₂ bude roven síle F_g. Pro velikosti sil potom platí:

Stejný otáčivý účinek znamená, že součet momentů sil F₁ a F₂ vůči libovolné vybrané ose musí být stejný jako moment síly F_g vůči této ose. Vybereme-li si například osu procházející v místě závaží kolmo k pravítku, moment síly F_g je vůči této ose nulový, a momenty sil F₁ a F₂ budou proto mít stejnou velikost a opačný směr (aby jejich součet dal nulu):

d₁ a d₂ jsou vzdálenosti sil F₁ a F₂ od F_g. Určitě jste zjistili i experimentálně, že velikosti zatížení na koncích pravítka jsou nepřímo úměrné vzdálenostem příslušných konců od závaží.

Zvolíme-li si osu tak, aby procházela pravým okrajem pravítka, bude platit

odkud snadno vyjádříme velikost síly zatěžující levý konec:

Stejně určíme i velikost zatížení na druhém konci, zvolíme-li osu v levém okraji pravítka:

Dokážete nyní určit, jakou silou budou zatěžováni nosiči, jestliže ponesou skříň o výšce 2 m, šířce 1,2 m a hmotnosti 60 kg po schodišti se sklonem 20°? Řešení

Určitě už dokážete objasnit, proč může námraza na vodičích ohnout pevné sloupy vysokého napětí. Vysvětlení