|
FyzWeb síly |
||||||||||||
Násobenà vektorů
kde F je velikost pĹŻsobĂcĂ sĂly a d je kolmá vzdálenost tĂ©to sĂly od osy otáčenĂ. TakĂ© jsme se dozvÄ›dÄ›li, Ĺľe moment sĂly je vektor a kromÄ› jeho velikosti tedy záležà i na jeho smÄ›ru. FyzikovĂ© pouĹľĂvajĂ elegantnĂ matematickĂ˝ zpĹŻsob, jak vyjádĹ™it moment sĂly M pĹ™Ămo jako vektor pomocĂ vztahu:
kde r je polohovĂ˝ vektor pĹŻsobištÄ› sĂly F vzhledem k ose otáčenĂ jako počátku (nenĂ tedy dokonce ani potĹ™eba zjišťovat kolmou vzdálenost sĂly). Co tedy znamená uvedenĂ˝ zápis s kĹ™ĂĹľkem? Jedná se o takzvanĂ˝ vektorovĂ˝ souÄŤin dvou vektorĹŻ, kterĂ˝ je pro dva vektory
definován vztahem:
Z definiÄŤnĂho vztahu vyplĂ˝vá, Ĺľe vĂ˝sledek vektorovĂ©ho souÄŤinu je opÄ›t vektor. PodĂvejte se na pomĹŻcku, jak lze rychle vyjádĹ™it sloĹľky vĂ˝slednĂ©ho vektoru. VĂ˝slednĂ˝ vektor vektorovĂ©ho souÄŤinu má zajĂmavĂ© vlastnosti, kterĂ© se pĹ™esnÄ› hodĂ napĹ™Ăklad právÄ› pro moment sĂly. Je vĹľdy kolmĂ˝ na dva násobenĂ© vektory, pĹ™iÄŤemĹľ jeho smÄ›r závisĂ na poĹ™adĂ násobenĂ vektorĹŻ. (VektorovĂ˝ souÄŤin tedy nenĂ komutativnĂ operace!) SmÄ›r mĹŻĹľeme urÄŤit napĹ™Ăklad pomĹŻckou s pravou rukou: PĹ™iloĹľĂme-li pravou ruku kolmo k vektorĹŻm tak, Ĺľe prsty směřujĂ od špiÄŤky prvnĂho násobenĂ©ho vektoru ke špiÄŤce druhĂ©ho, pak vztyÄŤenĂ˝ palec ukazuje smÄ›r vĂ˝slednĂ©ho vektoru, viz následujĂcĂ obrázek. Ĺkáme, Ĺľe prvnĂ násobenĂ˝, druhĂ˝ násobenĂ˝ a vĂ˝slednĂ˝ vektor (v tomto poĹ™adĂ) tvořà takzvanĂ˝ pravotoÄŤivĂ˝ systĂ©m. PĹ™i prohozenĂ násobenĂ˝ch vektorĹŻ se zmÄ›nĂ vĂ˝slednĂ˝ vektor na opaÄŤnĂ˝. Velikost souÄŤinovĂ©ho vektoru c se dá spoÄŤĂtat
jako
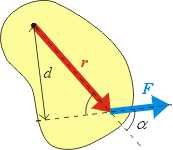
kde a, b jsou velikosti násobenĂ˝ch vektorĹŻ, a je Ăşhel, kterĂ˝ tyto vektory svĂrajĂ. UvedenĂ˝ vztah zcela odpovĂdá našemu jednoduchĂ©mu vztahu pro vĂ˝poÄŤet velikosti momentu sĂly. Podle pravoĂşhlĂ©ho trojĂşhelnĂku na vedlejšĂm obrázku totiĹľ mĹŻĹľeme psát:
VyjádĹ™Ăme-li si dále vektory na obrázku ve sloĹľkách
mĹŻĹľeme spoÄŤĂtat z definice vektorovĂ©ho souÄŤinu sloĹľky vĂ˝slednĂ©ho vektoru c:
VidĂme, Ĺľe vĂ˝slednĂ˝ vektor má nenulovou pouze sloĹľku ve smÄ›ru osy z, to znamená, Ĺľe je skuteÄŤnÄ› kolmĂ˝ na rovinu xy, ve kterĂ© ležà vektory a a b. Nakonec mĹŻĹľeme urÄŤit takĂ© velikost vĂ˝slednĂ©ho vektoru
která vycházĂ, jak jsme pĹ™edpokládali, rovna ploše rovnoběžnĂku. TĂm jsme ukázali, Ĺľe zavedenĂ© vztahy si opravdu odpovĂdajĂ a Ĺľe definice vektorovĂ©ho souÄŤinu (jako operace se sloĹľkami vektorĹŻ) má i správnou geometrickou interpretaci.
KromÄ› zmiĹnĂ©ho momentu sĂly se vektorovĂ˝ souÄŤin ve fyzice pouĹľĂvá pro vyjádĹ™enĂ dalšĂch veliÄŤin, jako je napĹ™Ăklad moment hybnosti, nebo magnetická sĂla pĹŻsobĂcĂ na pohybujĂcĂ se nabitou částici. Vedle uvedenĂ©ho vektorovĂ©ho souÄŤinu se běžnÄ› (a relativnÄ› ÄŤastÄ›ji) pouĹľĂvá ještÄ› jinĂ˝ takzvanĂ˝ skalárnĂ souÄŤin dvou vektorĹŻ. ÄŚĂm se lišà skalárnĂ a vektorovĂ˝ souÄŤin vektorĹŻ? HlavnĂm rozdĂlem kromÄ› zpĹŻsobu zápisu je, Ĺľe vĂ˝sledkem skalárnĂho souÄŤinu (jak název napovĂdá) je skalár a ne vektor. SkalárnĂ souÄŤin dvou vektorĹŻ a, b zapisujeme teÄŤkou mezi vektory a jeho hodnotu urÄŤujeme ze vztahu
kde a, b jsou velikosti skalárnÄ› násobenĂ˝ch vektorĹŻ, a je Ăşhel, kterĂ˝ násobenĂ© vektory svĂrajĂ. Typickou ukázkou skalárnĂho souÄŤinu je napĹ™Ăklad definiÄŤnĂ vztah pro práci W vykonanou silou F pĹ™i posunutĂ danĂ©m vektorem s:
Uvedený skalárnà součin můžeme vyjádřit jako
Z poslednĂho vztahu a obrázku je zĹ™ejmĂ© jakou roli zde hraje skalárnĂ souÄŤin - násobĂ vzdálenost uraĹľenou pĹ™edmÄ›tem se sloĹľkou sĂly ve smÄ›ru pohybu: Fcosa. To je rozumnĂ©, protoĹľe právÄ› tato sloĹľka koná skuteÄŤnÄ› práci. Pokud bude vektor sĂly F kolmĂ˝ na smÄ›r pohybu, je tato sloĹľka nulová a sĂla v danĂ©m smÄ›ru nekoná žádnou práci.
|
||||||||||||


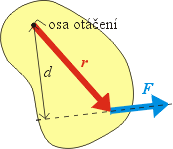 V kapitole o kroutivĂ©m momentu jsme poÄŤĂtali velikost
momentu sĂly M podle jednoduchĂ©ho vztahu
V kapitole o kroutivĂ©m momentu jsme poÄŤĂtali velikost
momentu sĂly M podle jednoduchĂ©ho vztahu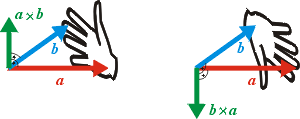
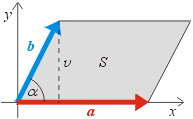 Dalšà zajĂmavou vlastnostĂ vyuĹľĂvanou ve fyzice i v
matematice je, Ĺľe velikost vĂ˝slednĂ©ho vektoru vektorovĂ©ho souÄŤinu odpovĂdá
ÄŤĂselnÄ› ploše rovnoběžnĂku urÄŤenĂ©ho násobenĂ˝mi vektory. Na obrázku
vlevo jsou násobené vektory a a b zvoleny "šikovně"
v rovinÄ› xy, pro plochu S zobrazenĂ©ho rovnoběžnĂku odtud mĹŻĹľeme psát:
Dalšà zajĂmavou vlastnostĂ vyuĹľĂvanou ve fyzice i v
matematice je, Ĺľe velikost vĂ˝slednĂ©ho vektoru vektorovĂ©ho souÄŤinu odpovĂdá
ÄŤĂselnÄ› ploše rovnoběžnĂku urÄŤenĂ©ho násobenĂ˝mi vektory. Na obrázku
vlevo jsou násobené vektory a a b zvoleny "šikovně"
v rovinÄ› xy, pro plochu S zobrazenĂ©ho rovnoběžnĂku odtud mĹŻĹľeme psát: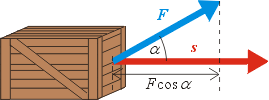 kde F je velikost pĹŻsobĂcĂ sĂly, s je vzdálenost
o kterou se předmět posunul, a je úhel,
kterĂ˝ svĂrala sĂla se smÄ›rem pohybu, viz vedlejšà obrázek.
kde F je velikost pĹŻsobĂcĂ sĂly, s je vzdálenost
o kterou se předmět posunul, a je úhel,
kterĂ˝ svĂrala sĂla se smÄ›rem pohybu, viz vedlejšà obrázek.