|
FyzWeb síly |
||||||||||||||||
Souřadnice a vektoryPokud chceme počítat složitější příklady z fyziky, je potřeba nějakým rozumným způsobem umět zapsat fyzikální veličiny. U skalárních veličin je to jednoduché - stačí zapsat jejich velikost s příslušnou jednotkou.
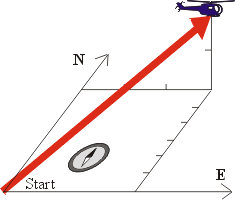
Nejčastěji používaný způsob - zápis ve složkách pravoúhlých (kartézských) souřadnic, si můžeme představit na jednoduchém příkladu. Představte si, že chcete například programovatelnému modelu vrtulníku zadat informace o tom, kterým směrem v prostoru má letět. Můžete to udělat tak, že mu sdělíte, kolik délkových jednotek má urazit každou sekundu směrem na sever, kolik jednotek východním směrem, a kolik jednotek směrem nahoru. Tak bude jednoznačně určena jeho poloha i vzdálenost, kterou urazil. To dohromady určuje takzvaný polohový vektor. Hodnoty jednotek délky uražených za nějaký čas v severním, východním a svislém směru určují takzvané složky polohového vektoru. Pokud bychom potřebovali, aby vrtulník letěl na jich, zadáme jednoduše složku v severním směru zápornou (stejně i s ostatními složkami). Na příkladu polohového vektoru vrtulníku vidíme, že je důležité zvolit si počátek a pevně dané směry, vůči kterým budeme určovat složky vektoru. Nejpoužívanější jsou právě pravoúhlé souřadnice dané třemi navzájem kolmými směry.
Vektor na obrázku tedy konkrétně zapíšeme jako:
V kapitole O vektorech jsme viděli, že například sčítání a odčítání vektorů jako matematická operace nezávisí na jejich umístění, vektory můžeme při zachovaném směru libovolně přesouvat. Pokud ale uvažujeme například výsledný účinek dvou sil působících na konkrétní těleso, zajímají nás také působiště sil. V obou případech na následujícím obrázku je součet sil působících na těleso nulový, v prvním případě však bude těleso v klidu, ve druhém se bude otáčet, protože je nenulový výsledný moment sil.
Síly na obrázku vlevo pouze roztahují těleso, síly na obrázku vpravo s tělesem otáčí. Operace s vektory ve složkáchZnáme-li složky vektoru, můžeme snadno určit velikost vektoru jako délku "příslušné šipky" pomocí pythagorovy věty:
Násobení vektoru skalárem se projeví tak, že uvažovaným skalárem vynásobíme jednotlivé složky:
Pokud si spočítáte velikost vektoru vynásobeného skalárem k, vyjde vám k - násobek délky původního vektoru, což odpovídá k - násobnému prodloužení šipky:
Sčítání vektorů znamená jednoduše sečíst jednotlivé složky vektorů. Stejně tak rozdíl dvou vektorů vyjádříme jako rozdíl odpovídajících složek.
i, j a k jsou přitom jednotkové vektory ve směru souřadnicových os x, y a z, viz vedlejší obrázek. (k zde tedy neznamená násobek vektoru!) Jiné typy souřadnic
Chceme-li například popsat, jak se mění polohový vektor ventilku kola vůči ose otáčení, bude se v polárních souřadnicích měnit pouze jedna složka - úhel j, složka r - velikost vektoru zůstává stejná. Pokud bychom chtěli stejný vektor popisovat v kartézských souřadnicích, budou se komplikovaně měnit obě složky vektoru.
Zkuste se zamyslet nad tím, kde by bylo výhodné použít válcové souřadnice.
Při popisu polohy na Zemi, kterou uvažujeme za kouli je velikost polohového vektoru (poloměr Země) konstantní a mění se pouze úhly q a j, které nazýváme zeměpisná šířka a zeměpisná délka. Kromě popsaných typů souřadnic se používají i další speciální souřadnice (například parabolické, hyperbolické, logaritmické...), ty však nejsou zdaleka tak časté.
|
||||||||||||||||


 Jak ale vyjádříme zároveň velikost i směr
vektorů?
Jak ale vyjádříme zároveň velikost i směr
vektorů?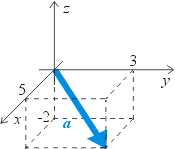 Na vedlejším obrázku je znázorněn
vektor v pravoúhlé
soustavě souřadnic se znázorněnými složkami. Matematicky zapisujeme vektor
ve složkách pomocí závorky:
Na vedlejším obrázku je znázorněn
vektor v pravoúhlé
soustavě souřadnic se znázorněnými složkami. Matematicky zapisujeme vektor
ve složkách pomocí závorky: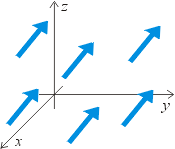 Pro počítání s vektory je důležité si uvědomit, že složky
vektoru určují pouze jeho velikost a směr. To znamená, že například všechny
šipky na vedlejším obrázku můžeme vyjádřit jako jeden vektor. Říkáme,
že jednotlivé šipky vyjadřují pouze různé umístění vektoru.
Pro počítání s vektory je důležité si uvědomit, že složky
vektoru určují pouze jeho velikost a směr. To znamená, že například všechny
šipky na vedlejším obrázku můžeme vyjádřit jako jeden vektor. Říkáme,
že jednotlivé šipky vyjadřují pouze různé umístění vektoru. 
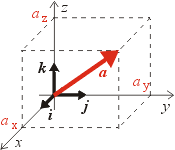 Uvedené operace s vektory umožňují zapsat vektor ještě jiným
způsobem, který se ve fyzice často používá - jako součet tří vektorů mířících
ve směrech souřadných os.
Uvedené operace s vektory umožňují zapsat vektor ještě jiným
způsobem, který se ve fyzice často používá - jako součet tří vektorů mířících
ve směrech souřadných os.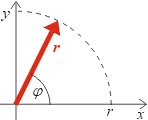 Mnohdy se vyplatí popisovat vektory v jiných než v pravoúhlých
kartézských souřadnicích. Mezi nejpoužívanější patří například polární
souřadnice. Ty popisují vektory pouze v rovině a to pomocí dvou čísel
- velikosti vektoru r a úhlu vektoru j,
který svírá se zvolenou polopřímkou (osou x), viz vedlejší obrázek.
Mnohdy se vyplatí popisovat vektory v jiných než v pravoúhlých
kartézských souřadnicích. Mezi nejpoužívanější patří například polární
souřadnice. Ty popisují vektory pouze v rovině a to pomocí dvou čísel
- velikosti vektoru r a úhlu vektoru j,
který svírá se zvolenou polopřímkou (osou x), viz vedlejší obrázek.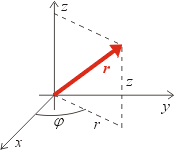 Přidáme-li k polárním souřadnicím ještě výšku z
nad zvolenou rovinou, dostaneme takzvané válcové nebo cylindrické
souřadnice, které se hodí pro popis objektů s válcovou symetrií, viz obrázek
vlevo. Vektor v těchto souřadnicích vyjádříme obdobně jako
u polárních souřadnic:
Přidáme-li k polárním souřadnicím ještě výšku z
nad zvolenou rovinou, dostaneme takzvané válcové nebo cylindrické
souřadnice, které se hodí pro popis objektů s válcovou symetrií, viz obrázek
vlevo. Vektor v těchto souřadnicích vyjádříme obdobně jako
u polárních souřadnic: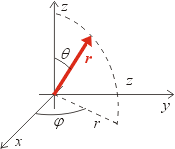 Dalším typem souřadnic, které určitě znáte například ze
zeměpisu jsou kulové nebo sférické souřadnice. Jak název
napovídá, používají se především při popisu kulově symetrických problémů.
Složky vektoru umístěného ve zvoleném počátku jsou opět délka r
vektoru a dále dva úhly q a j
měřené od dvou zvolených kolmých polopřímek, viz obrázek vpravo.
Vektor se pak zapisuje ve složkách jako:
Dalším typem souřadnic, které určitě znáte například ze
zeměpisu jsou kulové nebo sférické souřadnice. Jak název
napovídá, používají se především při popisu kulově symetrických problémů.
Složky vektoru umístěného ve zvoleném počátku jsou opět délka r
vektoru a dále dva úhly q a j
měřené od dvou zvolených kolmých polopřímek, viz obrázek vpravo.
Vektor se pak zapisuje ve složkách jako: