Kroutivý moment

Chcete překvapit své známé? Předveďte jim kouzelnou krabičku, která se dokáže po jedné niti libovolně spouštět dolů, nebo šplhat vzhůru podle vašeho přání. Při zatáhnutí za spodní provázek se krabička posunuje nahoru, při uvolnění klesá dolů.

Co se může skrývat v záhadné krabičce?

Asi by nebylo správné hned prozradit celé tajemství. Pokud zrovna nevíte, jak by mohla krabička fungovat, určitě vás časem něco napadne.

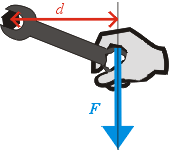
Pojďme se nyní místo přemýšlení o krabičce chvíli věnovat tomu, co se skrývá pod pojmy kroutivý moment nebo točivý moment a k čemu to může být dobré. O točivém momentu jste určitě slyšeli například v souvislosti s výkonem motorů automobilů. Čím větší je točivý moment motoru, tím větší "má motor sílu". Je však potřeba doplnit, že výkon nevyjadřuje přesně to samé jako točivý moment. Podrobnosti

Možná také víte, že každý šroub lze utahovat pouze s jistým maximálním kroutivým momentem, pokud tuto hodnotu překročíte, šroub se ukroutí.

Oba jmenované příklady se nějak týkají otáčení a my už víme, že otáčivý účinek na těleso charakterizuje veličina moment síly. A je to právě tato veličina, která popisuje silový účinek motoru na převodové ústrojí automobilu, nebo působení klíče na šroub při utahování. Kroutivý moment, točivý moment a moment síly tedy vyjadřují jednu fyzikální veličinu. Ve speciálním případě, kdy síla F, působící na těleso, leží v rovině kolmé k ose otáčení tělesa, můžeme vyjádřit velikost momentu této síly vzhledem k dané ose otáčení jako:

kde F je velikost působící síly, d je kolmá vzdálenost osy otáčení od přímky určené vektorem F. Vzdálenosti d se také říká rameno síly F. Z uvedeného vztahu je patrné, že jednotkou momentu síly je N.m.

Vyzkoušejte si, jak velký kroutivý moment dokážete vyvinout rukou. Návod

Zatím jsme se zmi�li pouze o velikosti momentu síly. Otáčíme-li ale nějakým tělesem, záleží také na tom, na kterou stranu s ním otáčíme. Při povolování a utahování uzávěru lahve můžeme působit stejně velkými silami, ale účinek je jiný.

Moment síly je proto vektor, který klademe do osy otáčení a jehož směr lze určit podle takzvaného pravidla pravé ruky: Uchopíme-li těleso (například uzávěr lahve) pravou rukou tak, že prsty ukazují směr otáčení, pak vztyčený palec ukazuje směr momentu síly. To znamená, že při utahování uzávěru lahve míří vektor momentu síly směrem dovnitř lahve, při povolování směrem ven, viz fotografie nahoře.

Na vedlejší fotografii je znázorněno silové působení nohy na pedál kola. Pokuste se určit velikost a směr momentu znázorněné síly F o velikosti 200 N, kterým je namáhána osa pedálů. Dále zkuste určit, jakou maximální silou může být napínán řetěz kola, jestliže nohou vyvineme na pedál sílu o velikosti maximálně 500 N. Páka od šlapky je dlouhá 18 cm, průměry zobrazených ozubených kol jsou 17 cm, 13 cm a 9 cm. šení

Víte, co je to momentový klíč a jak funguje momentový šroubovák?

Podívejte se, k čemu mohou být jmenované nástroje dobré.

Představte si nyní, že na nějaký otáčivý předmět působí více sil najednou.

Jaký bude jejich celkový otáčivý účinek?

Máte pravdu, jestliže odpovídáte, že musíme sečíst momenty jednotlivých sil vůči dané ose otáčení. Jenom nesmíme zapomenout na to, že moment síly je vektor, a musíme tedy jednotlivé momenty sčítat jako vektory. Výsledný moment síly M působící na těleso můžeme tedy zapsat jako

kde M₁, M₂, M₃, ...M_n jsou momenty jednotlivých sil, které na těleso působí.

Dokážete určit, jaký je výsledný moment sil nohou působících na pedály kola znázorněných na vedlejší fotografii vzhledem k ose otáčení pedálů? Zobrazené síly mají velikosti F₁ = 250 N, F₂ = 100 N, páka šlapky je dlouhá 18 cm.

Na správné řešení přijdete určitě snadno i sami.

Pokud se těleso, na které působí nějaké síly, vlivem těchto sil neotáčí, znamená to, že celkový moment působících sil vzhledem k ose otáčení je nulový:

Tomuto jednoduchému vztahu se říká momentová věta, a je důležitý právě v případech, kdy chceme spočítat, za jakých podmínek se těleso nebude otáčet pod vlivem působících sil. Poznámka

Vyzkoušejte si pomocí appletu, za jakých podmínek bude například vyvážená jednoduchá páka se závažím.

Víte už, co by se mohlo skrývat v kouzelné krabičce z úvodu stránky? Jste-li si jisti svým vlastním vysvětlením, podívejte se jak si takovou krabičku vyrobit.