|
FyzWeb srážky a rotace |
||||||||||||
O vektorech
Víte jakou funkci měl předmět na fotografii? Jedná se o takzvané "váhy", které se používali pro zapřahání koní do kočárů, vozů, pluhů a jiných zemědělských potahů. Dva koně byli zapřaženi postranními řemeny za krátká břevna a jejich síla se přenášela pomocí dlouhého břevna na vůz. Není asi potřeba dlouze vysvětlovat, že celková síla působící na vůz byla v takovém případě rovna součtu sil, kterými táhli koně.
V uvedeném příkladu použití vah u povozů jsme využili známou skutečnost, že rovnoběžné síly (kterými působí koně na váhy) se dají jednoduše sečíst a dostaneme tak celkovou sílu působící na vůz. Jak se však bude sčítat větší množství sil, které míří různými směry a které další operace lze provádět s vektorovými veličinami? Pojďme si některé takové operace vysvětlit. Násobení vektoru skalárem
Pokud násobíme vektor záporným skalárem, funguje vše stejně (šipka se prodlužuje nebo zkracuje) pouze směr šipky bude opačný jako na následujícím obrázku.
Speciálně, když vynásobíme vektor minus jedničkou, získáme stejně dlouhý vektor mířící opačným směrem, kterému se proto říká vektor opačný k původnímu.
Poznámka: Matematikové používají místo výrazu šipka raději pojem orientovaná úsečka, což samozřejmě nic nemění na významu tohoto pojmu. Sčítání vektorůVezměme si opět jako příklad vektorů síly. Působíme-li na nějaký předmět
dvěma silami a chceme vědět, jaký je jejich společný účinek na tento předmět,
potřebujeme tyto dvě síly vektorově sečíst a získat tak jejich výslednici. Jak takový součet vypadá si vyzkoušejte pomocí interaktivního
Pokud potřebujeme sečíst více vektorů, sečteme jednoduše libovolné dva, k jejich výsledku přičteme další vektor, a tak dále, až vyčerpáme všechny vektory. Asi jste si také všimli, že sčítání vektorů lze provádět technicky ještě jiným způsobem - přesouváním konce jednoho vektoru k začátku druhého.
Oběma metodami sčítání vektorů - doplněním na rovnoběžník i přikládáním začátku jednoho vektoru ke konci druhého vektoru bychom se měli dobrat ke stejnému výsledku. Rozmyslete si, že obě metody znamenají v podstatě totéž.
Podívejme se na některé speciální případy, které z uvedeného vztahu vycházejí: Sčítáme-li dva vektory mířící stejným směrem, dosadíme do vztahu úhel, který svírají a = 0°. Protože cos 0° = 1 dostaneme velikost výsledné síly:
To odpovídá známé skutečnosti, že výsledné působení dvou sil stejného směru je rovno jejich prostému součtu. Podobně pro síly mířící opačným směrem, kdy a = 180° (cos 180° = -1) dostáváme výslednou sílu rovnu rozdílu působících sil:
Pokud přitom vyjde velikost výsledné síly F záporná, znamená to pouze, že výslednice míří opačným směrem než F1 (tedy směrem F2). Pokud budeme sčítat dva kolmé vektory dosadíme do vztahu pro součet dvou vektorů a = 90° (cos 90° = 0) a získáme tak známou Pythagorovu větu, která zde vyjadřuje délku úhlopříčky obdélníku:
Odčítání vektorů
Je to snad dostatečně zřejmé i když si to napíšeme algebraicky:
Všimněte si, že při uvedených operacích jsme se nestarali o umístění vektorů a uvažovali jsme, že vycházejí ze stejného bodu, nebo že je můžeme libovolně přesouvat - důležité je pouze zachovat jejich velikost a směr nezměněný. Matematické operace s vektory tedy nezávisí na jejich poloze v prostoru. Teprve když budeme počítat s fyzikálními veličinami, například sčítat dvě konkrétní síly působící na nějaký předmět, budeme muset uvažovat také působiště těchto vektorů.
|
||||||||||||




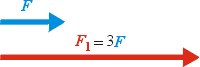 Víme už, že velikost vektoru se vyjadřuje délkou šipky, která znázorňuje
daný vektor - například sílu. Zvětšíme-li třikrát sílu, aniž bychom měnili
její směr, bude příslušná šipka třikrát delší, viz vedlejší obrázek.
Neznamená to nic jiného, než že jsme sílu F vynásobili
skalárem 3. Výslednou třikrát zvětšenou sílu F1
zapíšeme matematicky jednoduše jako:
Víme už, že velikost vektoru se vyjadřuje délkou šipky, která znázorňuje
daný vektor - například sílu. Zvětšíme-li třikrát sílu, aniž bychom měnili
její směr, bude příslušná šipka třikrát delší, viz vedlejší obrázek.
Neznamená to nic jiného, než že jsme sílu F vynásobili
skalárem 3. Výslednou třikrát zvětšenou sílu F1
zapíšeme matematicky jednoduše jako: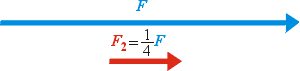 Stejně jednoduše můžeme násobit jakýkoli vektor libovolným skalárem.
Jestliže potřebujeme vektor vydělit skalárem - například čtyřikrát
zmenšit původní sílu, uděláme to tak, že sílu vynásobíme jednou čtvrtinou,
což je totéž, viz obrázek vpravo. Matematicky můžeme zapsat výslednou sílu F2 jako:
Stejně jednoduše můžeme násobit jakýkoli vektor libovolným skalárem.
Jestliže potřebujeme vektor vydělit skalárem - například čtyřikrát
zmenšit původní sílu, uděláme to tak, že sílu vynásobíme jednou čtvrtinou,
což je totéž, viz obrázek vpravo. Matematicky můžeme zapsat výslednou sílu F2 jako: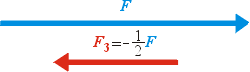
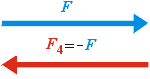
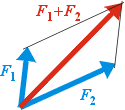 Pokud jste si pohráli s appletem, přišli jste možná sami na to, že
konstrukci výsledného součtového vektoru dvou vektorů můžeme provést
pomocí rovnoběžek - takzvaným doplněním na rovnoběžník.
Oba vektory umístíme do jednoho působiště a jejich koncovými body vedeme
rovnoběžky s vektory tak, že vytvoříme rovnoběžník. Součet obou vektorů
je potom vektor vycházející ze společného působiště a určený přeponou
rovnoběžníku, viz vedlejší obrázek.
Pokud jste si pohráli s appletem, přišli jste možná sami na to, že
konstrukci výsledného součtového vektoru dvou vektorů můžeme provést
pomocí rovnoběžek - takzvaným doplněním na rovnoběžník.
Oba vektory umístíme do jednoho působiště a jejich koncovými body vedeme
rovnoběžky s vektory tak, že vytvoříme rovnoběžník. Součet obou vektorů
je potom vektor vycházející ze společného působiště a určený přeponou
rovnoběžníku, viz vedlejší obrázek.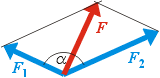 Zatím jsme si ukázali, jak sčítat vektory geometricky. Pokud známe
velikosti F1 a F2 dvou vektorů a úhel
Zatím jsme si ukázali, jak sčítat vektory geometricky. Pokud známe
velikosti F1 a F2 dvou vektorů a úhel 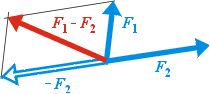 Umíme-li už sčítat vektory, je jejich odčítání jednoduché. Chceme-li
například od vektoru F1 odečíst vektor F2,
viz obrázek vpravo, uděláme z vektoru F2 vektor opačný a přičteme
ho k F1.
Umíme-li už sčítat vektory, je jejich odčítání jednoduché. Chceme-li
například od vektoru F1 odečíst vektor F2,
viz obrázek vpravo, uděláme z vektoru F2 vektor opačný a přičteme
ho k F1.