|
FyzWeb síly |
||||||||||||
O rovnováze
Takový jednoduchý mobil si můžete snadno a rychle udělat sami a vyzkoušet
pomocí něho své známé. Dokážete seřadit podle hmotností krabičky na úvodní fotografii? Svoji odpověď, která krabička je nejtěžší, a která nejlehčí, si můžete prakticky ověřit vyrobením vlastního mobilu. Dokážete také teoreticky vysvětlit, proč tomu tak má být (případně určit správné poměry hmotností krabiček)? Podle jakých pravidel byste řešili podobné složitější problémy, které byste si neměli možnost prakticky ověřit? Celý náš mobil je vyvážený a pokud se ani neotáčí, ani nepohybuje vzhledem k Zemi, říkáme, že se nachází v takzvané statické rovnováze. Aby bylo jakékoli těleso v rovnováze, musí splňovat dvě základní podmínky, se kterými jsme se konkrétně setkali už v případě rozkladu síly na dvě rovnoběžné složky v kapitole o rozkladu sil: I. Celkový součet všech sil působících na těleso je nulový:
II. Celkový součet všech momentů sil působících na těleso je nulový:
Síly i momenty ve vztazích pro rovnováhu jsou vektory, při dosazování jejich velikostí tedy musíme uvažovat směr sil a smysl otáčení způsobeného momenty sil.
Rukou ohnutou v lokti držíme kbelík vody o hmotnosti mk = 10 kg. Zajímá nás, jakou silou je přitom napínán úpon bicepsu, který drží zvednutou ruku s kýblem. Hmotnost předloktí budeme uvažovat přibližně mp = 1,8 kg.
Všechny síly působí ve svislém směru. První podmínku rovnováhy (rovnost sil) můžeme tedy zapsat pomocí velikostí sil, přičemž síly mířící zvoleným směrem (nahoru) budou kladné, opačně mířící síly záporné:
Podmínku rovnováhy momentů sil vzhledem k ose procházející loketním kloubem lze potom zapsat jako:
a je úhel který svírá předloktí s vodorovnou rovinou, momenty sil způsobující otáčení jedním vybraným směrem jsou kladné, momenty otáčející předloktí opačným směrem záporné. V podmínce pro rovnováhu momentů sil nepočítáme se silou F, protože její moment vzhledem k vybrané ose otáčení je nulový. Díky tomu, že jsou všechny síly rovnoběžné, můžeme také vykrátit člen cosa, který je u všech momentů stejný (výsledek nezávisí na úhlu ohnutí předloktí). Z druhé podmínky tak můžeme hned vyjádřit velikost síly, kterou působí biceps na předloktí:
Dosazením do první podmínky (rovnováhy sil) pak můžeme vyjádřit také velikost síly, kterou působí pažní kost v lokti na kost loketní:
Po dosazení uvažovaných hodnot vychází síla napínající úpon bicepsu přibližně Ft = 943 N a síla působící na loketní kloub F = 825 N. Z výsledků je vidět, jak velkými silami mohou být namáhány kosti, šlachy a svaly při zátěži. Proto také může při náhlém přetížení, například během sportovního výkonu, snadno dojít k natažení či natržení šlach, eventuelně k vymknutí kloubu.
Jak velká je hmotnost protizávaží? Jak těžký náklad může jeřáb zvedat na konci čtyřicetimetrového ramena, aby se nepřevrhnul? Přijdete sami na správné řešení?
Podíváte-li se kolem sebe, zjistíte, že spousta nástrojů, které běžně používáme, využívá nějakého pákového mechanismu. Všechny takové mechanismy využívají principů statické rovnováhy. Na fotografii jsou například vyobrazeny nůžky na stříhání plechu, složené z několika pohyblivých pák.
Proč je ostří nůžek mírně prohnuté? Zkuste dané problémy vyřešit nejdříve sami, teprve potom se podívejte
se na možná Nyní už byste měli být schopni odpovědět na úvodní problém, která z krabiček našeho "mobilu", zobrazeného na začátku stránky, je nejtěžší a která nejlehčí, případně jaké jsou poměry jejich hmotností. Řešení
|
||||||||||||




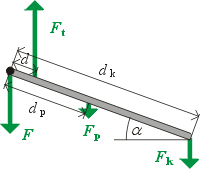 Celé předloktí si můžeme představit jako jednoduchou páku, na kterou působí
čtyři síly jako na vedlejším obrázku: Fk = mk
g (g je tíhové zrychlení o velikosti přibližně
10 m.s-2) je tíha kýble s vodou, Fp = mp
g je tíha předloktí, F je síla, kterou působí
kost paže v loketním kloubu na předloktí, Ft je
tahová síla bicepsu. Vzdálenosti působišť jednotlivých sil od osy otáčení
procházející loketním kloubem můžeme uvažovat přibližně d = 4 cm,
dp = 15 cm, dk = 35 cm.
Celé předloktí si můžeme představit jako jednoduchou páku, na kterou působí
čtyři síly jako na vedlejším obrázku: Fk = mk
g (g je tíhové zrychlení o velikosti přibližně
10 m.s-2) je tíha kýble s vodou, Fp = mp
g je tíha předloktí, F je síla, kterou působí
kost paže v loketním kloubu na předloktí, Ft je
tahová síla bicepsu. Vzdálenosti působišť jednotlivých sil od osy otáčení
procházející loketním kloubem můžeme uvažovat přibližně d = 4 cm,
dp = 15 cm, dk = 35 cm.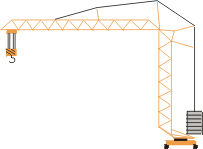

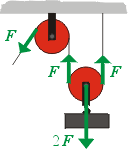 Rovnováhy sil a momentů sil člověk už dávno využívá také při
konstrukci různých kladkových mechanismů. Na vedlejším obrázku je znázorněno schéma
nejjednoduššího kladkostroje, sestaveného z jedné pevné a jedné volné
kladky. Velikosti sil působících z obou stran na kladku jsou stejné, protože
se rovnají velikosti jejich momentů (to platí pro pevnou i volnou kladku). Z
podmínky pro rovnováhu sil potom vyplývá, že volná kladka zvedá břemeno
silou dvakrát větší, než působíme na konec provazu.
Rovnováhy sil a momentů sil člověk už dávno využívá také při
konstrukci různých kladkových mechanismů. Na vedlejším obrázku je znázorněno schéma
nejjednoduššího kladkostroje, sestaveného z jedné pevné a jedné volné
kladky. Velikosti sil působících z obou stran na kladku jsou stejné, protože
se rovnají velikosti jejich momentů (to platí pro pevnou i volnou kladku). Z
podmínky pro rovnováhu sil potom vyplývá, že volná kladka zvedá břemeno
silou dvakrát větší, než působíme na konec provazu.
