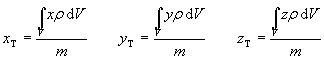Úvod

Celkové shrnutí

Shrnutí jednotlivých kapitol

Síla patří mezi takzvané vektorové fyzikální veličiny. To znamená, že vždy můžeme určit její velikost a směr.

Velikost síly měříme siloměrem, její jednotkou je 1 N (jeden newton).

Různé mincíře a mnohé druhy vah jsou v podstatě siloměry, které měří tíhu předmětů.

Graficky se síla jakožto vektor znázorňuje šipkou udávající směr, délka šipky znázorňuje velikost síly. Důležitým bodem je začátek šipky označující působiště síly - místo, ve kterém síla působí na předmět.

Fyzikální veličiny, u kterých určujeme pouze hodnotu a ne směr, se nazývají skaláry. V textu rozlišujeme vektory od skalárů tučným písmem, nebo šipkou nad příslušným písmenem.

Všechny druhy sil mají původ ve čtyřech základních interakcích, mezi které patří gravitační, elektromagnetická, slabá a silná jaderná interakce.

Síly působící na těleso mohou způsobit jeho deformaci,  pohyb, nebo změnu pohybu tělesa . Tuhé těleso je takové, které se pod účinky sil nedeformuje.

Pohyby těles můžeme rozdělit na posuvné (translační) a otáčivé (rotační). K roztočení tělesa na místě je třeba působení takzvané dvojice sil.

Otáčivý účinek na tělesa popisuje fyzikální veličina moment síly. Moment síly vzhledem k příslušné ose otáčení je tím větší, čím větší je síla otáčející tělesem a čím větší je (kolmá) vzdálenost této síly od osy otáčení.

Složit dvě nebo více sil působících na těleso znamená nahradit je jedinou silou, která má na těleso stejný účinek.

Při skládání dvou a více sil stejného směru má výsledná síla velikost rovnu součtu velikostí skládaných sil. Při skládání dvou sil opačného směru má výslednice směr stejný jako větší ze skládaných sil a velikost rovnu rozdílu velikostí skládaných sil.

Skládat lze pouze síly působící na stejné těleso. Při vzájemném silovém působení dvou těles na sebe platí zákon akce a reakce, který říká, že dvě tělesa na sebe působí navzájem stejně velkými silami opačného směru, které současně vznikají a zanikají.

Sílu lze rozložit na takzvané složky v daných směrech (například vodorovném a svislém), složky působí dohromady na těleso stejně jako původní síla. Rozkládání síly na složky je tedy opačný proces ke skládání.

V praxi se velmi často využívá rozkladu sil - například u klínových nástrojů, ve stavebnictví u klenutých prvků, u jednoduchých strojů, jako je nakloněná rovina a šroub apod.

Páka, na kterou působí dvě síly F₁ a F₂, je v rovnováze (vyvážená), je li splněn vztah

,

kde d₁ a d₂ jsou vzdálenosti sil od osy otáčení. Síly musí mít navíc opačný otáčivý účinek - každá se snaží otáčet pákou na opačnou stranu.

V praxi se často používají páky ke zvětšení síly, zvýšení rychlosti, nebo změně směru síly. Široké uplatnění nalézají například jako násady a ramena u mnoha druhů náčiní, jako páčidla a zvedací mechanismy, na jejich funkci jsou založeny také všechny kladky, kladkostroje a soukolí nebo některé druhy vah.

Těžiště je působiště výsledné tíhové síly působící na těleso.

Experimentálně můžeme nalézt polohu těžiště například podpíráním (podepřené vyvážené těleso má těžiště svisle nad bodem podepření) nebo zavěšováním v různých polohách (těžiště volně zavěšeného tělesa se nachází svisle pod bodem zavěšení - na těžnici).

Těleso se může nacházet ve třech rovnovážných polohách - stálé (stabilní), volné (indiferentní), nebo vratké (labilní).

Stabilita tělesa v určité rovnovážné poloze znamená práci, kterou musíme vynaložit k překlopení tělesa do jiné rovnovážné polohy. Stabilita proto závisí na šířce základny tělesa, hmotnosti tělesa a poloze těžiště (výšce nad základnou a vzdáleností od překlápěcí hrany).

Při vynásobení vektoru skalárem (konstantou) k se pouze k krát zvětší velikost vektoru. Při násobení vektoru záporným číslem se obrátí jeho směr. Vynásobením vektoru minus jedničkou získáme opačný vektor.

Dva vektory různého směru můžeme geometricky sečíst doplněním na rovnoběžník, nebo přesunem jednoho vektoru svým začátkem ke konci druhého vektoru. Více vektorů sčítáme postupně stejným způsobem.

Velikost výsledného součtového vektoru spočítáme jako příslušnou úhlopříčku rovnoběžníku určeného sčítanými vektory.

Odečíst vektor znamená přičíst opačný vektor.

Matematické operace s vektory nezávisí na jejich poloze v prostoru.

Kroutivý nebo točivý moment jsou další používaná označení pro vektorovou veličinu moment síly, jejíž velikost je určena vztahem:

F je velikost síly působící na těleso, d je (kolmá) vzdálenost této síly od příslušné osy otáčení. Směr vektoru momentu síly můžeme určit pomocí pravidla pravé ruky.

Celkový moment více sil působících na těleso je dán vektorovým součtem momentů jednotlivých působících sil:

Momentová věta vyjadřuje skutečnost, že otáčivý účinek více sil působících na těleso se ruší, je-li výsledný moment působících sil vzhledem k dané ose otáčení nulový:

V praxi je moment síly důležitou charakteristikou například motorů. Momentový klíč slouží k utahování šroubů (vrutů) určitým definovaným momentem síly.

Rozložit sílu na dvě složky v daných směrech znamená najít v těchto směrech takové dvě síly, jejichž složením (vektorovým součtem) dostaneme původní sílu.

Při rozkladu síly na dvě rovnoběžné složky je součet velikostí rozkladných sil roven velikosti původní síly. Poměr velikostí rozkladných sil je přitom opačný k poměru vzdáleností rozkladných sil od původní síly.

V praxi je třeba počítat s tím, že složky síly (například tíhové), kterými jsou namáhány součásti různých objektů a zařízení, mohou být mnohonásobně větší, než samotná působící síla.

Těleso se nachází ve statické rovnováze, jsou-li splněny dvě podmínky:

1. Součet všech sil působících na těleso je nulový:

2. Součet momentů všech sil působících na těleso je nulový:

Rovnice sestavené na základě uvedených vztahů umožňují nalézt řešení konkrétních příkladů mechanických systémů, které se nacházejí ve statické rovnováze.

Pro soustavu těles o hmotnostech m₁, m₂,...,m_n, jejichž vzdálenosti (vzdálenosti jejich těžišť) od zvoleného počátku jsou v jednom určitém směru po řadě x₁, x₂,...,x_n, vypočítáme vzdálenost těžiště soustavy od daného počátku a v daném směru ze vztahu:

Podle uvedeného vztahu můžeme spočítat polohu těžiště nepravidelného tělesa, které lze rozdělit (alespoň myšlenkově) na více pravidelných těles o známé hmotnosti a poloze těžiště.

Vektor má v kartézské soustavě souřadnic obecně tři nezávislé složky - ve směrech souřadnicových os. Vektor potom zapisujeme v těchto složkách jako

nebo jako součet příslušných násobků jednotkových vektorů ve směrech souřadnicových os:

Složky vektoru vypovídají pouze o směru a velikosti vektoru, nepopisují jeho umístění v prostoru.

Při vynásobení vektoru skalárem se tímto skalárem násobí jednotlivé složky:

Při sčítání (odčítání) dvou vektorů se sčítají (odčítají) odpovídající si složky:

Kromě kartézských souřadnic se používají další souřadné systémy, mezi nejpoužívanější patří polární souřadnice (pouze dvojrozměrné), dále válcové (cylindrické) souřadnice a kulové (sférické) souřadnice.

Výsledkem vektorového součinu dvou vektorů a, b je vektor definovaný ve složkách vztahem:

Výsledný vektor je kolmý na rovinu určenou násobenými vektory, jeho směr lze určit pomocí pravé ruky - vektory a, b, c (v tomto pořadí) tvoří takzvaný pravotočivý systém. Velikost výsledného vektoru

odpovídá číselně ploše rovnoběžníku určeného vektory o velikostech a, b, které spolu svírají úhel a.

Výsledkem skalárního součinu dvou vektorů o velikostech a, b, které spolu svírají úhel a je skalár daný vztahem:

Mnoho fyzikálních veličin je určeno vektorovým, nebo skalárním součinem jiných fyzikálních veličin.

Hmotný střed tělesa je bod definovaný ve zvoleném kartézském systému souřadnicemi:

V a m je objem a hmotnost tělesa, r je funkce popisující prostorové rozložení hustoty tělesa (u homogenních těles je konstantní). V praktických příkladech často stačí počítat pouze jednu nebo dvě souřadnice, ostatní jsou určeny symetrií tělesa.

Poloha hmotného středu tělesa odpovídá poloze těžiště tohoto tělesa v homogenním tíhovém poli.

Úvod